Spearman、Pearson、Euclidean、Cosine、Jaccard,用来衡量不同数据之间的相似性或差异性
1. Spearman相关系数:
- 用于衡量两个变量之间的排序关系的强度和方向。
- Spearman相关系数关注的是两个变量的排序一致性,而不关心具体的数值大小。
- 值的范围为-1到1,1表示完全正相关,-1表示完全负相关,0表示无相关性。
- 常用于统计分析和数据之间的单调关系检测。
2. Pearson相关系数
- 衡量不同数据之间相似性或差异性的一种方法。
- 它主要用于度量两个变量之间的线性相关性。具体来说,Pearson相关系数反映的是两个变量的协同变化趋势,即当一个变量增加或减少时,另一个变量是否以相似的方式变化。
- 值的范围为-1到1,1表示完全正相关,-1表示完全负相关,0表示无相关性,即两个变量之间没有线性关系。
Spearman与Pearson之间的区别:
- Pearson 适用于两个变量之间的线性关系,而Spearman适用于单调关系。
- Pearson 处理变量的数据原始值,而 Spearman 处理数据排序值(需要先做变换,transform)
- 如果散点图表明“可能是单调的,可能是线性的”关系,最好的选择是 Spearman 而不是 Pearson。即使数据证明是完全线性的,用 Spearman 也不会造成信息丢失。但是,如果不是完全线性但使用 Pearson 系数,会丢失 Spearman 可以捕获的信息,是否单调。http://相关系数: Pearson vs Spearman - ml-butcher的文章 - 知乎 https://zhuanlan.zhihu.com/p/465213120
3. 欧氏距离(Euclidean distance):
- 衡量两个点之间的“直线”距离,计算公式为点之间各坐标差的平方和的平方根。
- 在多维空间中常用来衡量两个样本的差异,距离越大表示差异越大。
- 常用于聚类算法(如K-Means)和最近邻算法(如KNN)。
- 另:欧氏距离可以应用于两个向量之间的比较。它常用于衡量两个向量在多维空间中的“直线”距离,也就是说,两个向量之间的差异程度。

4. 余弦相似度(Cosine similarity):
- 衡量两个向量之间的角度相似性,计算公式为两个向量点积除以其模长乘积。
- 取值范围为[-1, 1],1表示完全相似,0表示不相关,-1表示完全相反。
- 常用于文本相似性分析(如TF-IDF向量化后的文本比较)和推荐系统中。
- 在PPI网络中,使用随机游走生成的节点向量时,比较向量相似性通常更适合使用余弦距离。
- 原因如下:
-
向量的方向更重要:
- 在PPI网络中,随机游走生成的向量反映了节点之间的拓扑结构和邻接关系。此时,向量的方向(即节点在网络中的相对位置)往往比向量的绝对大小更重要。
- 余弦距离衡量的是向量之间的夹角,即方向上的相似性,而不考虑向量的长度。因此,适用于比较基于网络拓扑生成的向量。
-
降低向量长度的影响:
- PPI网络中的节点连接数(度)可能会有较大差异,导致生成的向量大小不同。余弦距离在这种情况下可以消除向量长度对相似性计算的影响,只比较向量的方向。
- 欧氏距离会受到向量长度的影响,如果节点度数差异较大,使用欧氏距离可能会导致相似性评估不准确。
-
在网络嵌入应用中的常用做法:
- 在大多数基于图嵌入的应用中(如Node2Vec、DeepWalk等),余弦相似度是常见的选择。它在衡量网络节点的相似性时表现更为稳定。
5. Jaccard相似度(Jaccard similarity):
- 衡量两个集合之间的相似性,计算公式为两个集合交集的大小除以并集的大小。
- 取值范围为[0, 1],1表示完全相似,0表示完全不同。
- 常用于集合相似性比较,如文本、标签或分类数据的比较。
相关文章:

Spearman、Pearson、Euclidean、Cosine、Jaccard,用来衡量不同数据之间的相似性或差异性
1. Spearman相关系数: 用于衡量两个变量之间的排序关系的强度和方向。Spearman相关系数关注的是两个变量的排序一致性,而不关心具体的数值大小。值的范围为-1到1,1表示完全正相关,-1表示完全负相关,0表示无相关性。常…...
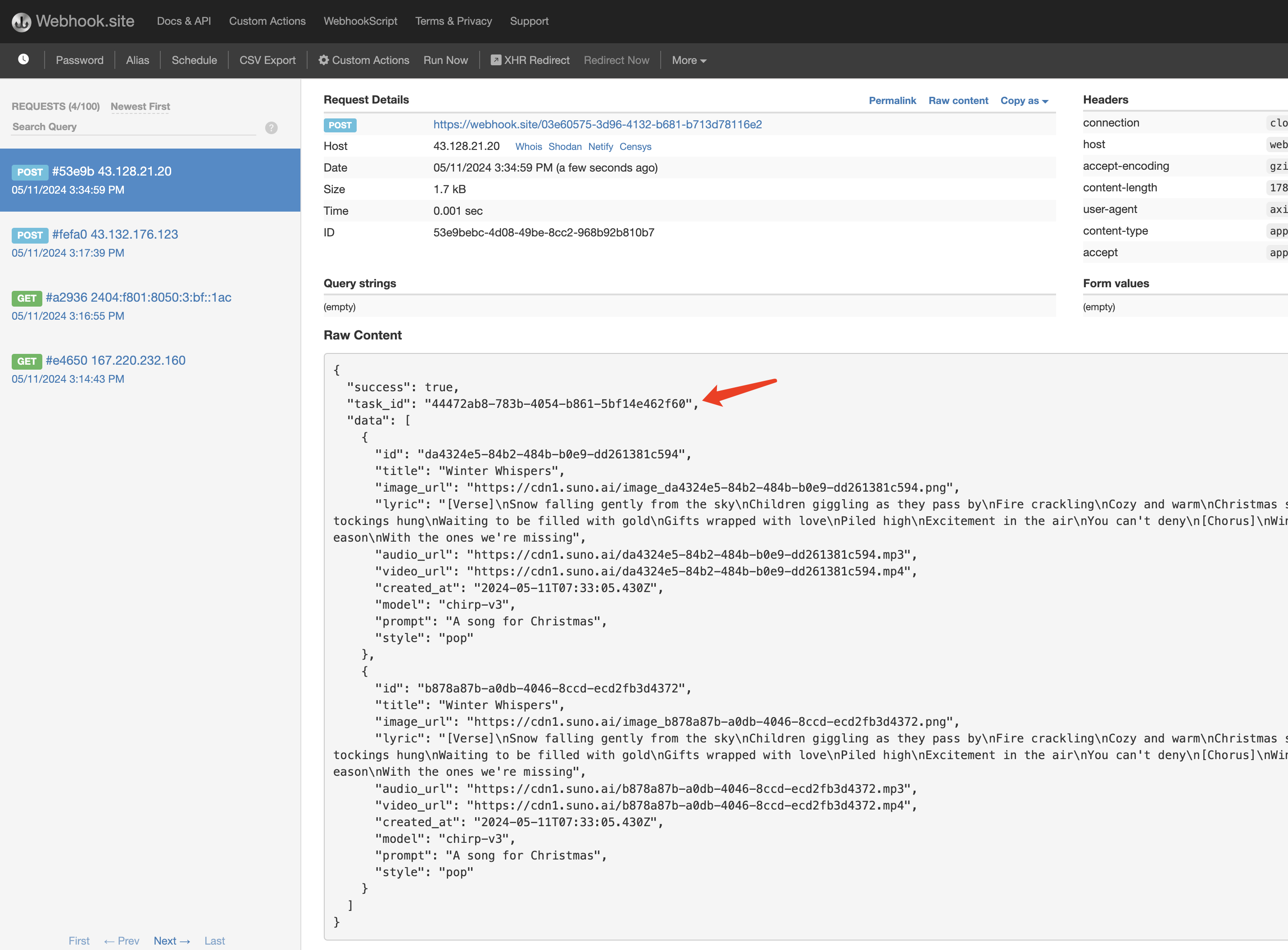
Suno 歌曲生成 API 对接说明
随着 AI 的应用变广,各类 AI 程序已逐渐普及。AI 已逐渐深入到人们的工作生活方方面面。而 AI 涉及的行业也越来越多,从最初的写作,到医疗教育,再到现在的音乐。 Suno 是一个专业高质量的 AI 歌曲和音乐创作平台,用户…...

详细且系统的Spring Boot应用开发
为了帮助大家更好地理解如何使用Spring Boot来构建一个基础的Web应用程序,我将通过一个简单的例子来进行说明。这个例子将是一个基本的RESTful API服务,用于管理图书信息。 项目准备 1. 开发环境设置(这个我之前有发文,这里就不详…...
)
线程支持库(C++11)
线程支持库包含了线程,互斥锁,线程条件变量(class thread),定义于<thread> 线程提供一个并发的实例,需要对应一个“线程函数” 线程的主要任务就是去执行这个"线程函数" 既然线程需要提供一个线程函数,…...

【计网】深入理解NAT机制,内网穿透与内网打洞,代理服务
我没胆量犯错 才把一切错过 --- 林夕 《我对不起我》--- 一文了解NAT机制,代理服务,内网穿透 1 再谈 NAT 机制2 内网穿透与内网打洞3 代理服务器 1 再谈 NAT 机制 NAT机制我们在解决IP地址不足的问题中提到过。为了解决IP地址不足的问题,采…...

C# 创建型设计模式----工厂模式
1 、什么是工厂模式 简单来说就是由一个对象去生成不同的对象,工厂模式是用工厂方法代替new操作的一种模式。工厂方法封装了多个相关联类的new方法,每次实例化这些类的时候不需要new多次,只需要调用工厂类的对应方法即可实例化这些类&#x…...

java中Scanner的nextLine和next方法
思考,输入1 2 3 4 5加上enter,输出什么 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc new Scanner(System.in);int[][] m new int[2][2];for (int i 0; i < 2; i) {for (int j 0; j < 2;…...

2024年全国山洪径流模拟与洪水危险性评价技术及典型地区洪水淹没及损失分析
洪水淹没危险性(各种年遇型洪水淹没)是洪水损失评估、风险评估及洪水应急和管理规划等工作的重要基础。当前开展洪水危险性研究工作中的主要困难之一是水文资料稀缺,尤其是径流资料稀缺,既包括径流观测资料在时间上的短缺…...

CDC 同步数据需要的MySQL数据权限
授权命令如下: grant Replication client on *.* to username%; grant Replication slave on *.* to username%; flush privileges;...

Ubuntu20.04 更新Nvidia驱动 + 安装CUDA12.1 + cudnn8.9.7
一、概述 最近客户给了几台GPU服务器,长期放置落灰那种,然后想利用起来,所以上去看看了配置,系统是Ubuntu20.04,相关的驱动版本稍嫌老一些,所以需要更新Nvidia驱动,同时在安装CUDA和CUDNN,查看了显卡型号之后,打算使用onnxruntime进行推理,对比了版本,最后选择了CUD…...
算法自学 Lesson3 - 逻辑回归(LR)
目录 背景 一、适用数据集 1. 数据集选择 1.1 领域 1.2 数据集维度 1.3 记录行(样本数量) 2. 本文数据集介绍 3. 数据集下载 注意 二、逻辑回归的基本原理 1. 目的 2. Sigmoid 函数 3. 类别划分 4. 召回率 三、代码 1. 导入所需包&数…...

文件IO流
1.文件流概念 2.文件创建方式 3.常用方法 4.IO流原理 (1)InputStream,OutputStream, Reader, Writer四个都是抽象类,无法直接new, 需要由子类继承,然后new子类; (2)Reader和Writer…...

拥塞控制与TCP子问题(粘包问题,异常情况等)
拥塞控制 除了拥塞控制 以上的策越都是为了解决tcp 客户端和服务端提高效率,解决丢包的策略 但是拥塞控制是了为解决网络拥堵 出现了大面积丢包,我们发送方会判定是网络出现了问题? 丢包好解决,我们直接采用超时重传&#…...

stm32入门教程--DMA 超详细!!!
目录 简介 工作模式 1、数据转运DMA 2、ADC扫描模式DMA 简介 工作模式 1、数据转运DMA 这个例子的任务是将SRAM的数组DataA,转运到另一个数组DataB中,这个基本结构里的各个参数应该如何配置呢? 首先是外设站点和存储器站点的起始地址、…...

【使用Flask构建RESTful API】从零开始开发简单的Web服务!
使用Flask构建RESTful API:从零开始开发简单的Web服务 引言 随着Web应用程序的广泛使用,RESTful API已成为现代Web服务的核心技术之一。通过RESTful API,我们可以轻松地创建、读取、更新和删除(CRUD)数据,…...

用sdcc给51单片机编译C程序
学习单片机大部分人用的是Keil uVision,虽然好用,可大部分人用的是盗版,其实单片机程序小的话,完全可以用文本编辑器(推荐notepad)编写,然后用免费的sdcc来编译,下面介绍一下大致的过程。 sdcc…...

Java Lock LockSupport 源码
前言 相关系列 《Java & Lock & 目录》(持续更新)《Java & Lock & LockSupport & 源码》(学习过程/多有漏误/仅作参考/不再更新)《Java & Lock & LockSupport & 总结》(学习总结/最新…...

Elasticsearch基础操作入门
阅前准备知识 学习 Elasticsearch (简称 ES) 的查询方式,建议从以下几个步骤入手: 理解 Elasticsearch 的基础概念 首先要了解 Elasticsearch 的核心概念,例如: Index(索引):相当于数据库中…...

跨域问题解决办法
跨域问题在Web开发中是一个常见的问题,特别是在前后端分离的开发模式下。以下是一些解决跨域问题的办法: 一、后端配置CORS(跨来源资源共享) CORS是一种机制,它使用额外的HTTP头来告诉浏览器一个网页的当前来源&…...

【数据结构与算法】力扣 23. 合并 K 个升序链表
题干描述 23. 合并 K 个升序链表 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 示例 1: 输入: lists [[1,4,5],[1,3,4],[2,6]] 输出: [1,1,2,3,4,4,5,6]…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
