当前位置： 首页 > news >正文

软考：常用协议和端口号

news 2026/1/30 5:22:38

常用协议及其对应的端口号如下：

  1. TCP/IP协议：

    • TCP（传输控制协议）：端口号为6
    • UDP（用户数据报协议）：端口号为17

  2. 网络应用协议：

    • HTTP（超文本传输协议）：端口号为80
    • HTTPS（安全的超文本传输协议）：端口号为443
    • FTP（文件传输协议）：数据传输端口为20，控制信令传输端口为21
    • TFTP（简单文件传输协议）：端口号为69，使用UDP连接
    • SMTP（简单邮件传输协议）：端口号为25
    • POP3（邮局协议版本3，负责邮件的接受）：端口号为110
    • Telnet：端口号为23
    • DNS（域名系统）：端口号为53，支持TCP和UDP

  3. 数据库和中间件协议：

    • Oracle数据库服务：端口号为1521
    • MySQL：端口号为3306
    • WebLogic：默认端口号为7001
    • WebSphere：默认端口号为9080
    • JBoss：默认端口号为8080
    • Tomcat：默认端口号为8080
    • SSH（安全外壳协议）：端口号为22

  4. 其他协议：

    • DHCP（动态主机配置协议）：服务器端端口号为67，客户机端端口号为68
    • SNMP（简单网络管理协议）：端口号为161，使用UDP
    • NTP（网络时间协议）：端口号为123，使用UDP
    • SMB/CIFS（服务器消息块/公共互联网文件系统）：端口号为445
    • RADIUS（远程认证拨号用户服务）：端口号为1645，使用UDP
    • L2TP（层2隧道协议）：端口号为1701，使用UDP
    • PPTP（点对点隧道协议）：端口号为1723，使用TCP

这些协议和端口号在分布式系统、网络通信和中间件中扮演着重要的角色。

相关文章：

软考：常用协议和端口号

常用协议及其对应的端口号如下： TCP/IP协议： TCP（传输控制协议）：端口号为6UDP（用户数据报协议）：端口号为17 网络应用协议： HTTP（超文本传输协议）…...

编程日记 2024/10/30 3:08:07

Linux更改符号链接

目录 1. 删除旧链接 2. 创建新的符号链接 例如我的电脑上有两个版本的cuda，11.8和12.4 1. 删除旧链接 rm cuda 2. 创建新的符号链接 ln -s /usr/local/cuda-11.8/ /usr/local/cuda...

编程日记 2024/10/30 3:06:05

int main(int argc,char* argv[])详解

#include <stdio.h> //argc 是指命令行输入参数的个数; //argv[]存储了所有的命令行参数, //arg[0]通常指向程序中的可执行文件的文件名。在有些版本的编译器中还包括程序文件所在的路径。 //如:"d:\Production\Software\VC_2005_Test\Win32控制台应用程序\Vc_T…...

编程日记 2024/10/30 3:05:04

单片机原理及应用笔记：C51流程控制语句与项目实践

作者介绍 周瑞康&#xff0c;男&#xff0c;银川科技学院&#xff0c;计算机人工智能学院&#xff0c;2022级计算机科学与技术8班本科生&#xff0c;单片机原理及应用课程第八组。 指导老师&#xff1a;王兴泽 电子邮箱2082545622qq.com 前言&#xff1a; 本篇文章是参考《…...

编程日记 2024/10/30 3:03:01

大数据日志处理框架ELK方案

介绍应用场景大数据ELK日志框架安装部署 一&#xff0c;介绍 大数据日志处理框架ELK&#xff08;Elasticsearch、Logstash、Kibana&#xff09;是一套完整的日志集中处理方案&#xff0c;以下是对其的详细介绍&#xff1a; 一、Elasticsearch&#xff08;ES&#xff09; 基本…...

编程日记 2024/10/30 2:59:56

VQGAN（2021-06：Taming Transformers for High-Resolution Image Synthesis）

论文&#xff1a;Taming Transformers for High-Resolution Image Synthesis 1. 背景介绍 2022年中旬&#xff0c;以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上&#xff0c;在更早的一年之前&#xff0c;就有了一个能根据文字生成高清图片的模型——VQGAN…...

编程日记 2024/10/30 2:58:55

docker中使用ros2humble的rviz2不显示问题

这里写目录标题 docker中使用ros2humble的rviz2不显示问题删除 Docker 镜像和容器删除 Docker 容器Linux服务器下查看系统CPU个数、核心数、(make编译最大的)线程数总结&#xff1a; RVIZ2 不能显示数据集 docker中使用ros2humble的rviz2不显示问题 问题描述&#xff1a; roo…...

编程日记 2024/10/30 2:56:53

【AIGC】2024-arXiv-Lumiere：视频生成的时空扩散模型

2024-arXiv-Lumiere: A Space-Time Diffusion Model for Video Generation Lumiere&#xff1a;视频生成的时空扩散模型摘要1. 引言2. 相关工作3. Lumiere3.1 时空 U-Net (STUnet)3.2 空间超分辨率的多重扩散 4. 应用4.1 风格化生成4.2 条件生成 5. 评估和比较5.1 定性评估5.2 …...

编程日记 2024/10/30 2:55:51

正则表达式：文本处理的强大工具

正则表达式是一种强大的文本处理工具&#xff0c;它允许我们通过定义一系列的规则来匹配、搜索、替换或分割文本。在编程、文本编辑、数据分析和许多其他领域中&#xff0c;正则表达式都扮演着重要的角色。本文将介绍正则表达式的基本概念、语法和一些实际应用。 正则表达式的…...

编程日记 2024/10/30 2:54:50

Doris单机安装

1、安装包下载 官网地址&#xff1a;https://doris.apache.org/zh-CN/docs/gettingStarted/quick-start/ 下载地址&#xff1a;https://apache-doris-releases.oss-accelerate.aliyuncs.com/apache-doris-3.0.2-bin-x64.tar.gz 2、操作系统环境准备 #环境准备 cat /proc/cp…...

编程日记 2024/10/30 2:53:49

ubuntu内核更新导致显卡驱动掉的解决办法

方法1&#xff0c;DKMS指定内核版本 用第一个就行 1&#xff0c;借鉴别人博客解决方法 2&#xff0c;借鉴别人博客解决方法 方法2&#xff0c;删除多于内核的方法 系统版本&#xff1a;ubuntu20.24 这个方法是下下策&#xff0c;如果重装驱动还是不行&#xff0c;就删内核在…...

编程日记 2024/10/30 2:52:47

【Java数据结构】树】

【Java数据结构】树 一、树型结构1.1 概念1.2 特点1.3 树的类型1.4 树的遍历方式1.5 树的表示形式1.5.1 双亲表示法1.5.2 孩子表示法1.5.3 孩子双亲表示法1.5.4 孩子兄弟表示法 二、树型概念&#xff08;重点&#xff09; 此篇博客希望对你有所帮助&#xff08;帮助你了解树&am…...

编程日记 2024/10/30 2:51:45

Java面试题——微服务篇

1.微服务的拆分原则/怎么样才算一个有效拆分 单一职责原则&#xff1a;每个微服务应该具有单一的责任。这意味着每个服务只关注于完成一项功能&#xff0c;并且该功能应该是独立且完整的。最小化通信&#xff1a;尽量减少服务之间的通信&#xff0c;服务间通信越少&#xff0c…...

编程日记 2024/10/30 2:50:44

Python 中 print 函数输出多行并且选择对齐方式

代码 # 定义各类别的标签和对应数量 categories ["class0", "class1", "class2", "class3", "class4", "class5"] counts [4953, 547, 5121, 8989, 6077, 4002]# 设置统一的列宽 column_width 10# 生成对齐后…...

编程日记 2024/10/30 2:48:41

书生营L0G3000 Git 基础知识

任务1: 破冰活动&#xff1a;自我介绍 用vi就行了 按照教程来就好了 git会报错密码&#xff0c;输入的时候换成token就好了 https://stackoverflow.com/questions/68775869/message-support-for-password-authentication-was-removed 提交。&#xff08;github上预览自己的…...

编程日记 2024/10/30 2:47:40

【C++初阶】模版入门看这一篇就够了

文章目录 1. 泛型编程2. 函数模板2. 1 函数模板概念2. 2 函数模板格式2. 3 函数模板的原理2. 4 函数模板的实例化2. 5 模板参数的匹配原则2. 6 补充&#xff1a;使用调试功能观察函数调用 3. 类模板3 .1 类模板的定义格式3. 2 类模板的实例化 1. 泛型编程 在C语言中&#xff0…...

编程日记 2024/10/30 2:46:39

Spring Bean创建流程

Spring Bean 创建流程图 大家总是会错误的理解Bean的“实例化”和“初始化”过程&#xff0c;总会以为初始化就是对象执行构造函数生成对象实例的过程&#xff0c;其实不然&#xff0c;在初始化阶段实际对象已经实例化出来了&#xff0c;初始化阶段进行的是依赖的注入和执行一…...

编程日记 2024/10/30 2:43:36

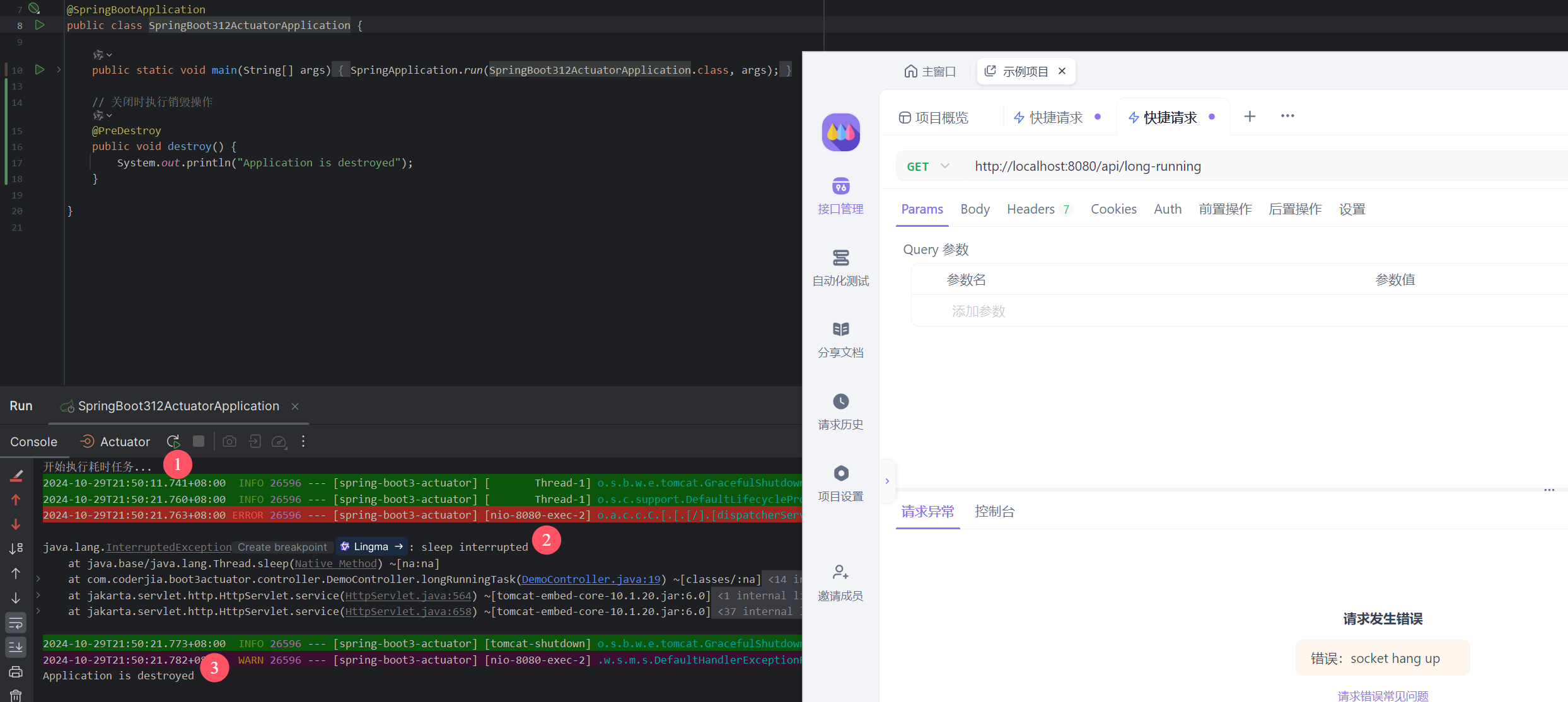
重学SpringBoot3-怎样优雅停机

更多SpringBoot3内容请关注我的专栏&#xff1a;《SpringBoot3》 期待您的点赞&#x1f44d;收藏⭐评论✍ 重学SpringBoot3-怎样优雅停机 1. 什么是优雅停机&#xff1f;2. Spring Boot 3 优雅停机的配置3. Tomcat 和 Reactor Netty 的优雅停机机制3.1 Tomcat 优雅停机3.2 Reac…...

编程日记 2024/10/30 2:42:34

【数据结构】顺序表和链表

1.线性表 我们在C语言当中学过数组&#xff0c;其实呢&#xff0c;数组可以实现线性表&#xff0c;线性表理解上类似于数组&#xff0c;那么什么是线性表呢&#xff1f;线性表是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使 用的数据结构&#xff0c;常见…...

编程日记 2024/10/30 2:41:32

Training language models to follow instructions with human feedback解读

前置知识方法数据集结论 前置知识 GPT的全称是Generative Pre-Trained Transformer&#xff0c;预训练模型自诞生之始&#xff0c;一个备受诟病的问题就是预训练模型的偏见性。因为预训练模型都是通过海量数据在超大参数量级的模型上训练出来的&#xff0c;对比完全由人工规则…...

编程日记 2024/10/30 2:39:30

Chapter03-Authentication vulnerabilities

文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

编程新知 2026/1/30 2:34:09

日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻

在如今就业市场竞争日益激烈的背景下&#xff0c;越来越多的求职者将目光投向了日本及中日双语岗位。但是&#xff0c;一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧&#xff1f;面对生疏的日语交流环境&#xff0c;即便提前恶补了…...

编程新知 2026/1/24 8:20:07

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/1/20 23:25:54

Go 语言并发编程基础：无缓冲与有缓冲通道

在上一章节中&#xff0c;我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道&#xff0c;它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好&#xff0…...

编程新知 2026/1/29 3:25:02

JS手写代码篇----使用Promise封装AJAX请求

15、使用Promise封装AJAX请求 promise就有reject和resolve了&#xff0c;就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

编程新知 2025/12/16 3:15:21

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强：基于微服务与容器化的解决方案

在大数据时代&#xff0c;海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构&#xff0c;在处理大规模数据抓取任务时展现出强大的能力。然而&#xff0c;随着业务规模的不断扩大和数据抓取需求的日益复杂&#xff0c;传统…...

编程新知 2026/1/28 15:17:48

springboot 日志类切面，接口成功记录日志，失败不记录

springboot 日志类切面&#xff0c;接口成功记录日志&#xff0c;失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

编程新知 2026/1/21 19:28:26

xmind转换为markdown

文章目录 解锁思维导图新姿势&#xff1a;将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件&#xff08;ZIP处理&#xff09;2.解析JSON数据结构3&#xff1a;递归转换树形结构4&#xff1a;Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

编程新知 2025/12/15 17:19:38

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解

一、前言 在HarmonyOS 5的应用开发模型中&#xff0c;featureAbility是旧版FA模型&#xff08;Feature Ability&#xff09;的用法&#xff0c;Stage模型已采用全新的应用架构&#xff0c;推荐使用组件化的上下文获取方式&#xff0c;而非依赖featureAbility。 FA大概是API7之…...

编程新知 2025/10/9 0:45:56