前端算法:树(力扣144、94、145、100、104题)
目录
一、树(Tree)
1.介绍
2.特点
3.基本术语
4.种类
二、树之操作
1.遍历
前序遍历(Pre-order Traversal):访问根节点 -> 遍历左子树 -> 遍历右子树。
中序遍历(In-order Traversal):遍历左子树 -> 访问根节点 -> 遍历右子树(用于 BST 时可得到排序结果)。
后序遍历(Post-order Traversal):遍历左子树 -> 遍历右子树 -> 访问根节点。
层序遍历(Level-order Traversal):逐层访问树的节点,通常使用队列实现。
2.插入和删除
3.查找
三、树的力扣算法实战
1.144. 二叉树的前序遍历
2.94. 二叉树的中序遍历
3.145. 二叉树的后序遍历
4.100. 相同的树
5.104. 二叉树的最大深度
一、树(Tree)

1.介绍
树(Tree)是一种重要的数据结构,广泛应用于计算机科学中。它由节点组成,并且有一个根节点,其他节点通过边连接形成层级关系。
2.特点
- 层级关系:树结构是分层的,根节点位于顶层,每个节点可以有多个子节点。
- 无环性:树中不存在环,即从一个节点出发不可能回到该节点。
- 节点的子节点:每个节点可以有零个或多个子节点。
3.基本术语
- 根节点:树的顶层节点。
- 叶子节点:没有子节点的节点。
- 子节点:某个节点直接连接的下层节点。
- 兄弟节点:同一父节点的子节点。
- 高度:树的高度是从根节点到最深叶子节点的最长路径的边数。
4.种类
-
树(Tree):一般的树结构,没有特定的限制。
-
二叉树(Binary Tree):每个节点最多有两个子节点。
- 完全二叉树(Complete Binary Tree):除了最后一层外,其他层的节点都填满,最后一层的节点尽量向左排列。
- 满二叉树(Full Binary Tree):每个节点要么是叶子节点,要么有两个子节点。
- 非完全二叉树(Incomplete Binary Tree):不是完全二叉树的任意形式。
-
二叉搜索树(Binary Search Tree, BST):一种特殊的二叉树,左子树的所有节点值小于根节点,右子树的所有节点值大于根节点。
-
自平衡树(Self-balancing Tree):如 AVL 树和红黑树,保持树的高度平衡以优化查找效率。
-
N 叉树(N-ary Tree):每个节点可以有 N 个子节点的树结构。
-
Trie(前缀树):一种用于存储字符串的树,常用于快速查找和前缀匹配。
二、树之操作
1.遍历
前序遍历(Pre-order Traversal):访问根节点 -> 遍历左子树 -> 遍历右子树。
// 前序遍历preOrderTraversal(node) {if (node) {console.log(node.value);this.preOrderTraversal(node.left);this.preOrderTraversal(node.right);}}中序遍历(In-order Traversal):遍历左子树 -> 访问根节点 -> 遍历右子树(用于 BST 时可得到排序结果)。
// 中序遍历inOrderTraversal(node) {if (node) {this.inOrderTraversal(node.left);console.log(node.value);this.inOrderTraversal(node.right);}}后序遍历(Post-order Traversal):遍历左子树 -> 遍历右子树 -> 访问根节点。
// 后序遍历postOrderTraversal(node) {if (node) {this.postOrderTraversal(node.left);this.postOrderTraversal(node.right);console.log(node.value);}}
层序遍历(Level-order Traversal):逐层访问树的节点,通常使用队列实现。
// 层序遍历levelOrderTraversal() {if (!this.root) return;const queue = [this.root];while (queue.length > 0) {const node = queue.shift();console.log(node.value);if (node.left) queue.push(node.left);if (node.right) queue.push(node.right);}}2.插入和删除
插入:在二叉搜索树中,插入新节点时需要找到合适的位置,保证 BST 的性质。
// 插入insert(value) {const newNode = new TreeNode(value);if (this.root === null) {this.root = newNode;return;}this.insertNode(this.root, newNode);}insertNode(node, newNode) {if (newNode.value < node.value) {if (node.left === null) {node.left = newNode;} else {this.insertNode(node.left, newNode);}} else {if (node.right === null) {node.right = newNode;} else {this.insertNode(node.right, newNode);}}}删除:删除节点时可能需要重新调整树结构,以保持树的性质,尤其在 BST 中。
// 删除delete(value) {this.root = this.deleteNode(this.root, value);}deleteNode(node, value) {if (node === null) {return null;}if (value < node.value) {node.left = this.deleteNode(node.left, value);} else if (value > node.value) {node.right = this.deleteNode(node.right, value);} else {// 找到要删除的节点if (node.left === null && node.right === null) {return null; // 无子节点}if (node.left === null) {return node.right; // 只有右子节点}if (node.right === null) {return node.left; // 只有左子节点}// 找到右子树中的最小节点const minNode = this.findMinNode(node.right);node.value = minNode.value; // 替换值node.right = this.deleteNode(node.right, minNode.value); // 删除最小节点}return node;}3.查找
在树中查找节点的过程依赖于树的性质。对于二叉搜索树,可以通过比较节点值快速找到目标节点。
search(value) {return this.searchNode(this.root, value);}searchNode(node, value) {if (node === null) {return false;}if (value === node.value) {return true;}return value < node.value? this.searchNode(node.left, value): this.searchNode(node.right, value);}三、树的力扣算法实战
1.144. 二叉树的前序遍历
题目描述:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出:[1,2,4,5,6,7,3,8,9]
示例 3:
输入:root = []
输出:[]
示例 4:
输入:root = [1]
输出:[1]
解题思路:将二叉树进行先序遍历(中左右:根节点->左子树->右子树)
代码:
var preorderTraversal = function(root) {const arr = []const fun = (node) =>{if(node){arr.push(node.val)fun(node.left)fun(node.right)}}fun(root)return arr
};2.94. 二叉树的中序遍历
题目描述:给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3] 输出:[1,3,2]示例 2:
输入:root = [] 输出:[]示例 3:
输入:root = [1] 输出:[1]
解题思路:将二叉树进行中序遍历(左中右:左子树->根节点->右子树)
代码:
var inorderTraversal = function(root) {const arr = []const fun = (root) =>{if(!root) returnfun(root.left)arr.push(root.val)fun(root.right)}fun(root)return arr
};3.145. 二叉树的后序遍历
题目描述:给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出:[4,6,7,5,2,9,8,3,1]
示例 3:
输入:root = []
输出:[]
示例 4:
输入:root = [1]
输出:[1]
解题思路:将二叉树进行中序遍历(左右中:左子树->右子树->根节点)
代码:
var postorderTraversal = function(root) {const arr = []const fun = (root) =>{if(!root) returnfun(root.left)fun(root.right)arr.push(root.val)}fun(root)return arr
};4.100. 相同的树
题目描述:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:p = [1,2,3], q = [1,2,3] 输出:true示例 2:
输入:p = [1,2], q = [1,null,2] 输出:false示例 3:
输入:p = [1,2,1], q = [1,1,2] 输出:false
解题思路:首先判断两个节点是否都为空,是则返回true;如果一个为空一个不为空,则返回false,再判断两个节点的val值是否相同,不同返回false,依次进行传入两棵树的左节点和右节点
代码:
var isSameTree = function(p, q) {if(p === null && q === null) return true;if(p === null || q === null) return falseif(p.val !== q.val) return falsereturn isSameTree(p.left,q.left) && isSameTree(p.right,q.right)
};5.104. 二叉树的最大深度
题目描述:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:3示例 2:
输入:root = [1,null,2] 输出:2
解题思路: 首先判断树是否为空,空则返回0,将树放入栈中,以栈的长度为值进行遍历,将栈的长度定义一个值len,每循环一次计数器num+1,len--,依次弹出stack的栈中元素,判断是否有左右子节点,在将其压入栈中,最后返回num值
代码
var maxDepth = function(root) {if(!root) return 0const stack = [root]let num = 0while(stack.length){let len = stack.lengthnum++while(len--){const o = stack.shift()o.left && stack.push(o.left)o.right && stack.push(o.right)}}return num
};相关文章:

前端算法:树(力扣144、94、145、100、104题)
目录 一、树(Tree) 1.介绍 2.特点 3.基本术语 4.种类 二、树之操作 1.遍历 前序遍历(Pre-order Traversal):访问根节点 -> 遍历左子树 -> 遍历右子树。 中序遍历(In-order Traversal…...

深度学习速通系列:如何使用bert进行超长中文文本命名实体识别
要将超长中文文本按最大 BERT 输入长度进行分割,并使用 bert-chinese-ner 模型进行命名实体识别,可以遵循以下步骤。以下是一个 Python 代码示例,利用 Hugging Face 的 transformers 库来实现: 安装必要的库 如果你还没有安装 Hu…...

【感知模块】深度神经网络实现运动预测
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言运动预测(Motion Prediction)感知中的运动预测(深度神经网络)前言 认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长! …...

智能优化算法-蝗虫优化算法(GOA)(附源码)
目录 1.内容介绍 2.部分代码 3.实验结果 4.内容获取 1.内容介绍 蝗虫优化算法 (Grasshopper Optimization Algorithm, GOA) 是一种基于群体智能的元启发式优化算法,由Saremi等人于2017年提出。GOA模拟了蝗虫群的觅食、迁徙和社会互动行为,用于解决复杂…...

TVM前端研究--Relay
文章目录 深度学习IR梳理1. IR属性2. DL前端发展3. DL编译器4. DL编程语言Relay的主要内容一、Expression in Relay1. Dataflow and Control Fragments2. 变量3. 函数3.1 闭包3.2 多态和类型关系3.3. Call4. 算子5. ADT Constructors6. Moudle和Global Function7. 常量和元组8.…...

STM32外设应用
STM32是基于ARM Cortex-M系列内核的微控制器,具有高性能、低功耗和丰富的外设资源。其广泛应用于物联网、工业控制、智能家居和嵌入式系统等领域。本文将简要介绍STM32常用外设的功能及应用实例,帮助大家更好地理解和使用STM32外设。 1. GPIO࿰…...

Docker 部署 Jaeger
Jaeger 的主要作用如下: 分布式追踪 Jaeger 是一个开源的分布式追踪系统,用于监控和排查微服务架构中的复杂问题。它可以跟踪请求在不同服务之间的传播路径,帮助开发者理解系统中各个组件之间的调用关系。 性能分析 通过收集和分析请求的执行…...

使用Python和OpenCV实现火焰检测
使用Python和OpenCV实现火焰检测 项目解释: 此 Python 代码是使用 OpenCV、线程、声音和电子邮件功能的火灾探测系统的简单示例。 以下是它的功能的简单描述: 导入库:代码首先导入必要的库: cv2:用于图像和视频处理…...

uniapp基础笔记
与html区别 uni-app简单来说是 vue的语法 小程序的api。 文件结构 html <!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title><script type"text/javascript"></script><style t…...

函数基础,定义与调用。作用域,闭包函数
一、函数的定义与调用 函数是一段可重复使用的代码块,用于执行特定任务或计算等功能。它可以接受输入参数(形参),并根据参数执行操作后返回结果。 函数的定义 例如在 JavaScript 中可以这样定义函数: function fun…...
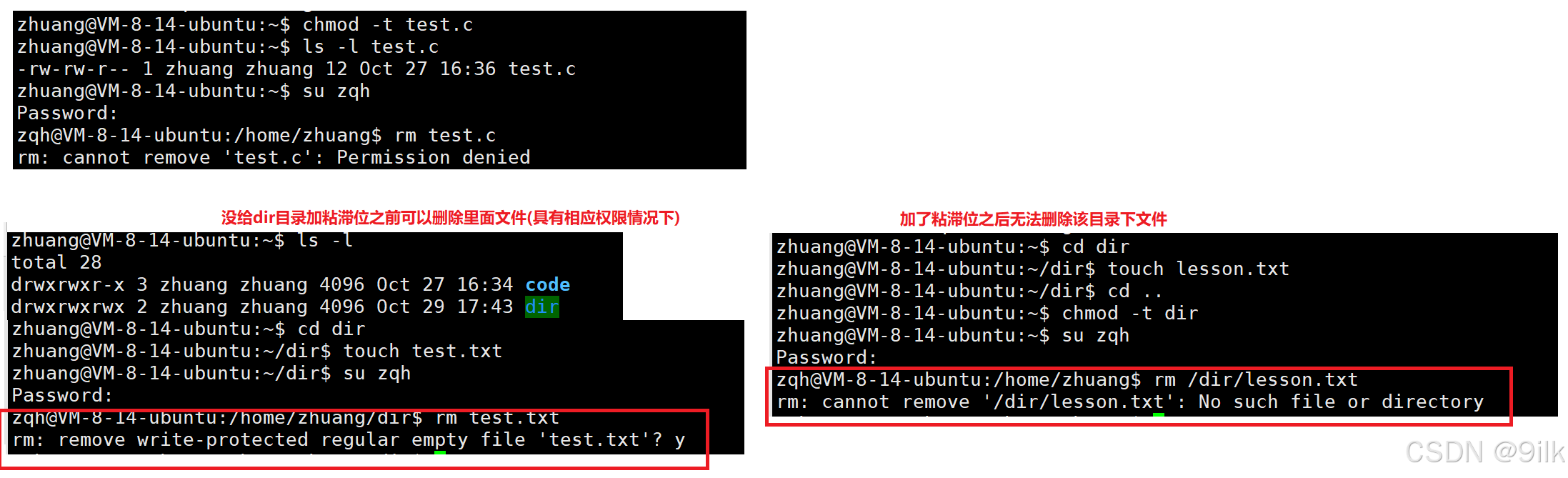
【Linux网络编程】 --- Linux权限理解
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: Linux网络编程 🏠 shell命令以及运行原理 📌 引入例子理解shell 假设八里村有一个人叫张三,他的父亲是这个村的村长…...

Qt/C++ 调用迅雷开放下载引擎(ThunderOpenSDK)下载数据资源
目录导读 前言ThunderOpenSDK 简介参考 xiaomi_Thunder_Cloud 示例ThunderOpenSDK 下载问题 前言 在对以前老版本的exe执行程序进行研究学习的时候,发现以前的软件是使用的ThunderOpenSDK这个迅雷开放下载引擎进行的项目数据下载,于是在网上搜索一番找到…...

深入详解 Java - Spring MVC
在 Java 企业级开发领域,Spring MVC 是一个极为重要的框架,它为构建强大、灵活且高效的 Web 应用程序提供了坚实的基础。本文将深入详解 Java 之 Spring MVC,带你领略其强大之处。 一、Spring MVC 概述 Spring MVC 是 Spring 框架的一个重要模块,全称为 Spring Web Model-V…...

Spring Boot技术中小企业设备管理系统设计与实践
6系统测试 6.1概念和意义 测试的定义:程序测试是为了发现错误而执行程序的过程。测试(Testing)的任务与目的可以描述为: 目的:发现程序的错误; 任务:通过在计算机上执行程序,暴露程序中潜在的错误。 另一个…...

动态渲染组件
引言 在现代前端开发中,动态渲染组件是一种常见的需求,特别是在构建复杂的应用程序时。动态渲染组件允许我们在运行时根据不同的条件或数据来决定渲染哪个组件,从而提高代码的灵活性和可维护性。本文将详细介绍如何在 Vue.js 中实现动态渲染…...

一个神秘的新图像生成模型red_panda出现 轻松击败Midjourney与OpenAI
一个神秘的新图像生成模型在众包人工分析基准测试中击败了 Midjourney、黑森林实验室和 OpenAI 的模型。这个名为"red_panda"的模型在人工分析的文本到图像排行榜上领先排名第二的黑森林实验室的 Flux1.1 Pro 约 40 个 Elo 分数。 Artificial Analysis 使用 Elo&…...
云计算平台上的DevOps实践
文章目录 什么是DevOps云计算平台上的DevOps优势自动化部署弹性伸缩地理分布 实施DevOps的关键组件版本控制系统持续集成/持续交付工具配置管理工具监控和日志管理 实践案例使用AWS CodePipeline进行持续集成/持续交付利用AWS Auto Scaling实现弹性使用AWS CloudFormation进行基…...

JS新功能之:全新 Set 方法
JavaScript 的内置Set类将新增一些方法,以便执行集合论中常见的操作,包括: Set.prototype.intersection(other):返回两个集合的交集。 Set.prototype.union(other):返回两个集合的并集。 Set.prototype.difference(o…...

Flume的安装配置
一、上传解压 tar -zxvf apache-flume-1.9.0-bin.tar.gz -C /usr/local/soft/#***在环境变量中增加如下命令,可以使用 soft 快速切换到 /usr/local/soft***alias softcd /usr/local/soft/ 二、配置环境变量 soft #重命名 mv apache-flume-1.9.0-bin/ flume-1.9.0…...

3.1.3 虚存页面的映射
3.1.3 虚存页面的映射 文章目录 3.1.3 虚存页面的映射3.1.3 虚存页面的映射MmCreateVirtualMapping()MmCreateVirtualMappingUnsafe()MiFlushTlb()MmDeleteVirtualMapping()MmPageOu…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...




