当前位置： 首页 > news >正文

一个神秘的新图像生成模型red_panda出现 轻松击败Midjourney与OpenAI

news 2026/2/8 13:32:06

一个神秘的新图像生成模型在众包人工分析基准测试中击败了 Midjourney、黑森林实验室和 OpenAI 的模型。这个名为"red_panda"的模型在人工分析的文本到图像排行榜上领先排名第二的黑森林实验室的 Flux1.1 Pro 约 40 个 Elo 分数。 Artificial Analysis 使用 Elo（一种最初开发用于计算棋手相对技术水平的排名系统）来比较其测试的各种模型的性能。

在这里插入图片描述
与社区人工智能基准Chatbot Arena类似，Artificial Analysis 通过众包的方式对模型进行排名。 对于图像模型，Artificial Analysis 会随机选择两个模型，并向它们提供一个独特的提示。 然后，它会展示提示和生成的图像，用户选择他们认为更能反映提示的图像。

在这里插入图片描述
当然，这个投票过程存在一定的偏见。 Artificial Analysis 的投票者大多是人工智能爱好者，他们的选择可能无法反映广大生成式人工智能用户的偏好。

不过，就生成速度而言，red_panda 也是排行榜上表现较好的模型之一。 该模型生成图像的时间中位数约为 7 秒，比 OpenAI 的 DALL-E 3 快 100 多倍。

在这里插入图片描述
那么，red_panda 从何而来？ 是哪家公司生产的？ 什么时候能发布？ 这些都是很好的问题。 不过，人工智能实验室越来越多地使用社区基准来在发布前鼓动人们的期待。

感谢大家花时间阅读我的文章，你们的支持是我不断前进的动力。期望未来能为大家带来更多有价值的内容，请多多关注我的动态！

相关文章：

一个神秘的新图像生成模型red_panda出现 轻松击败Midjourney与OpenAI

一个神秘的新图像生成模型在众包人工分析基准测试中击败了 Midjourney、黑森林实验室和 OpenAI 的模型。这个名为"red_panda"的模型在人工分析的文本到图像排行榜上领先排名第二的黑森林实验室的 Flux1.1 Pro 约 40 个 Elo 分数。 Artificial Analysis 使用 Elo&…...

编程日记 2024/10/30 3:26:37

云计算平台上的DevOps实践

文章目录 什么是DevOps云计算平台上的DevOps优势自动化部署弹性伸缩地理分布 实施DevOps的关键组件版本控制系统持续集成/持续交付工具配置管理工具监控和日志管理 实践案例使用AWS CodePipeline进行持续集成/持续交付利用AWS Auto Scaling实现弹性使用AWS CloudFormation进行基…...

编程日记 2024/10/30 3:24:27

JS新功能之：全新 Set 方法

JavaScript 的内置Set类将新增一些方法，以便执行集合论中常见的操作，包括： Set.prototype.intersection(other)：返回两个集合的交集。 Set.prototype.union(other)：返回两个集合的并集。 Set.prototype.difference(o…...

编程日记 2024/10/30 3:23:25

Flume的安装配置

一、上传解压 tar -zxvf apache-flume-1.9.0-bin.tar.gz -C /usr/local/soft/#***在环境变量中增加如下命令，可以使用 soft 快速切换到 /usr/local/soft***alias softcd /usr/local/soft/ 二、配置环境变量 soft #重命名 mv apache-flume-1.9.0-bin/ flume-1.9.0…...

编程日记 2024/10/30 3:21:23

3.1.3 虚存页面的映射

3.1.3 虚存页面的映射 文章目录 3.1.3 虚存页面的映射3.1.3 虚存页面的映射MmCreateVirtualMapping（）MmCreateVirtualMappingUnsafe（）MiFlushTlb（）MmDeleteVirtualMapping（）MmPageOu…...

编程日记 2024/10/30 3:20:21

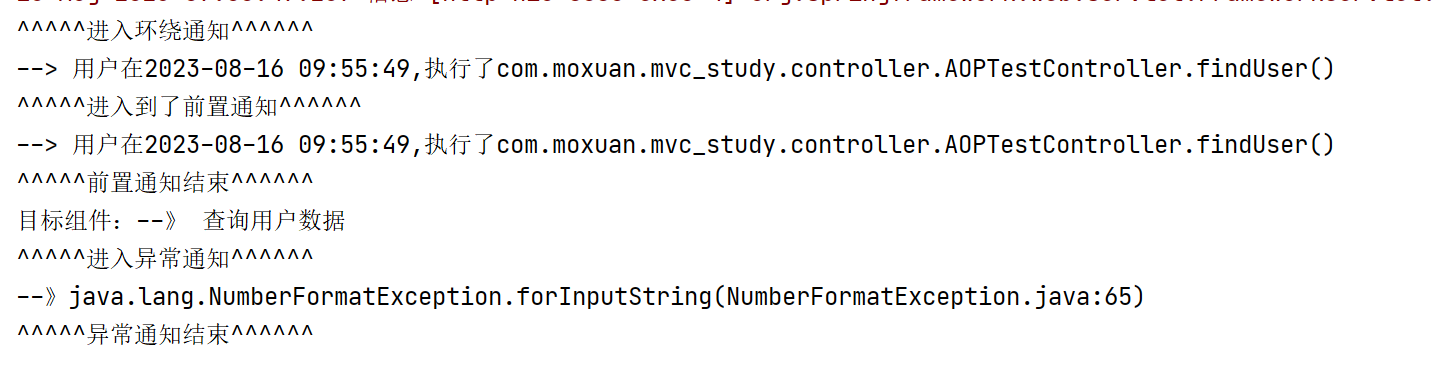
【SSM详细教程】-14-SpringAop超详细讲解

精品专题： 01.《C语言从不挂科到高绩点》课程详细笔记 https://blog.csdn.net/yueyehuguang/category_12753294.html?spm1001.2014.3001.5482 02. 《SpringBoot详细教程》课程详细笔记 https://blog.csdn.net/yueyehuguang/category_12789841.html?spm1001.20…...

编程日记 2024/10/30 3:19:21

虚拟机桥接模式连不上，无法进行SSH等远程操作

说明：以下情况在window10上遇到，解决后顺便做了个笔记，以防后续再次用到，也给同道中人提供一个解决方案 一、首先按照以下步骤进行检查 1、是否连接了对应的wifi 2、是否设置了桥接模式 3、上述1、2确认无误的情况下请查看右上…...

编程日记 2024/10/30 3:18:19

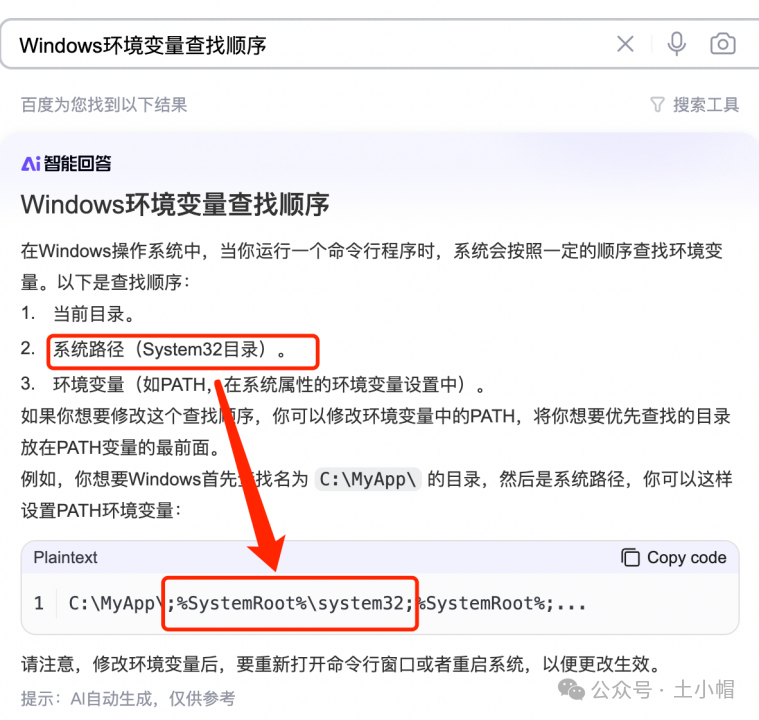
jmeter基础01-1_环境准备-windows系统安装jdk

课程大纲 一、步骤解说 step1. jdk官网下载 Java Downloads | Oracle step2. 安装/解压（二选一） 1. 安装包格式（后缀.exe/.msi/.dmg）：双击跟随界面向导安装，可以指定安装位置等。 2. 压缩包格式(后缀.z…...

编程日记 2024/10/30 3:15:15

第六天: C语言核心概念与实战技巧全解析

1 主函数（main） 大家好，今天我们来深入探讨一下C语言中非常特殊的一个函数——main函数。虽然大家对它并不陌生，但是它的重要性和特殊性值得我们再次回顾。 main函数的定义 main函数是我们整个C源程序的入口点。计算机在运行程…...

编程日记 2024/10/30 3:13:13

初始JavaEE篇——多线程（5）：生产者-消费者模型、阻塞队列

找往期文章包括但不限于本期文章中不懂的知识点： 个人主页：我要学编程程(ಥ_ಥ)-CSDN博客 所属专栏：JavaEE 文章目录 阻塞队列生产者—消费者模型生产者—消费者模型的优势：生产者—消费者模型的劣势： Java标准库中的阻…...

编程日记 2024/10/30 3:11:10

2024年下教师资格证面试报名详细流程❗

⏰ 重要时间节点： （一）下半年笔试成绩查询：11月8日10:00 （二）注册报名：11月8日10:00-11日18:00 （三）网上审核：11月8日10:00-11日18:00 （四&#x…...

编程日记 2024/10/30 3:10:09

软考：常用协议和端口号

常用协议及其对应的端口号如下： TCP/IP协议： TCP（传输控制协议）：端口号为6UDP（用户数据报协议）：端口号为17 网络应用协议： HTTP（超文本传输协议）…...

编程日记 2024/10/30 3:08:07

Linux更改符号链接

目录 1. 删除旧链接 2. 创建新的符号链接 例如我的电脑上有两个版本的cuda，11.8和12.4 1. 删除旧链接 rm cuda 2. 创建新的符号链接 ln -s /usr/local/cuda-11.8/ /usr/local/cuda...

编程日记 2024/10/30 3:06:05

int main(int argc,char* argv[])详解

#include <stdio.h> //argc 是指命令行输入参数的个数; //argv[]存储了所有的命令行参数, //arg[0]通常指向程序中的可执行文件的文件名。在有些版本的编译器中还包括程序文件所在的路径。 //如:"d:\Production\Software\VC_2005_Test\Win32控制台应用程序\Vc_T…...

编程日记 2024/10/30 3:05:04

单片机原理及应用笔记：C51流程控制语句与项目实践

作者介绍 周瑞康&#xff0c;男&#xff0c;银川科技学院&#xff0c;计算机人工智能学院&#xff0c;2022级计算机科学与技术8班本科生&#xff0c;单片机原理及应用课程第八组。 指导老师&#xff1a;王兴泽 电子邮箱2082545622qq.com 前言&#xff1a; 本篇文章是参考《…...

编程日记 2024/10/30 3:03:01

大数据日志处理框架ELK方案

介绍应用场景大数据ELK日志框架安装部署 一&#xff0c;介绍 大数据日志处理框架ELK&#xff08;Elasticsearch、Logstash、Kibana&#xff09;是一套完整的日志集中处理方案&#xff0c;以下是对其的详细介绍&#xff1a; 一、Elasticsearch&#xff08;ES&#xff09; 基本…...

编程日记 2024/10/30 2:59:56

VQGAN（2021-06：Taming Transformers for High-Resolution Image Synthesis）

论文&#xff1a;Taming Transformers for High-Resolution Image Synthesis 1. 背景介绍 2022年中旬&#xff0c;以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上&#xff0c;在更早的一年之前&#xff0c;就有了一个能根据文字生成高清图片的模型——VQGAN…...

编程日记 2024/10/30 2:58:55

docker中使用ros2humble的rviz2不显示问题

这里写目录标题 docker中使用ros2humble的rviz2不显示问题删除 Docker 镜像和容器删除 Docker 容器Linux服务器下查看系统CPU个数、核心数、(make编译最大的)线程数总结&#xff1a; RVIZ2 不能显示数据集 docker中使用ros2humble的rviz2不显示问题 问题描述&#xff1a; roo…...

编程日记 2024/10/30 2:56:53

【AIGC】2024-arXiv-Lumiere：视频生成的时空扩散模型

2024-arXiv-Lumiere: A Space-Time Diffusion Model for Video Generation Lumiere&#xff1a;视频生成的时空扩散模型摘要1. 引言2. 相关工作3. Lumiere3.1 时空 U-Net (STUnet)3.2 空间超分辨率的多重扩散 4. 应用4.1 风格化生成4.2 条件生成 5. 评估和比较5.1 定性评估5.2 …...

编程日记 2024/10/30 2:55:51

正则表达式：文本处理的强大工具

正则表达式是一种强大的文本处理工具&#xff0c;它允许我们通过定义一系列的规则来匹配、搜索、替换或分割文本。在编程、文本编辑、数据分析和许多其他领域中&#xff0c;正则表达式都扮演着重要的角色。本文将介绍正则表达式的基本概念、语法和一些实际应用。 正则表达式的…...

编程日记 2024/10/30 2:54:50

日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻

在如今就业市场竞争日益激烈的背景下&#xff0c;越来越多的求职者将目光投向了日本及中日双语岗位。但是&#xff0c;一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧&#xff1f;面对生疏的日语交流环境&#xff0c;即便提前恶补了…...

编程新知 2026/2/8 4:37:01

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】

微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来&#xff0c;Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

编程新知 2026/2/1 19:08:45

【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器

一.自适应梯度算法Adagrad概述 Adagrad&#xff08;Adaptive Gradient Algorithm&#xff09;是一种自适应学习率的优化算法&#xff0c;由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率&#xff0c;适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

编程新知 2026/1/26 18:15:24

QMC5883L的驱动

简介 本篇文章的代码已经上传到了github上面&#xff0c;开源代码 作为一个电子罗盘模块&#xff0c;我们可以通过I2C从中获取偏航角yaw&#xff0c;相对于六轴陀螺仪的yaw&#xff0c;qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

编程新知 2026/1/2 4:05:05

iPhone密码忘记了办？iPhoneUnlocker，iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版​分享

平时用 iPhone 的时候&#xff0c;难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵&#xff0c;或者买了二手 iPhone 却被原来的 iCloud 账号锁住&#xff0c;这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

编程新知 2026/1/29 10:22:28

LeetCode - 394. 字符串解码

题目 394. 字符串解码 - 力扣&#xff08;LeetCode&#xff09; 思路 使用两个栈&#xff1a;一个存储重复次数&#xff0c;一个存储字符串 遍历输入字符串&#xff1a; 数字处理&#xff1a;遇到数字时&#xff0c;累积计算重复次数左括号处理&#xff1a;保存当前状态&a…...

编程新知 2026/1/25 10:09:59

新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案

随着新能源汽车的快速普及&#xff0c;充电桩作为核心配套设施&#xff0c;其安全性与可靠性备受关注。然而&#xff0c;在高温、高负荷运行环境下&#xff0c;充电桩的散热问题与消防安全隐患日益凸显&#xff0c;成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

编程新知 2026/1/29 3:00:56

从零实现STL哈希容器：unordered_map/unordered_set封装详解

本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

编程新知 2026/1/31 12:47:25

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32