当前位置： 首页 > news >正文

【skywalking】maximum query complexity exceeded 3336 ＞ 3000

news 2026/2/10 1:35:39

问题

 skywalking相关版本信息

  • jdk：17
  • skywalking：10.1.0
  • apache-skywalking-java-agent：9.3.0
  • ElasticSearch : 8.8.2

问题描述

maximum query complexity exceeded 3336 > 3000

最大查询复杂度超过3336>3000

可能原因

  1. 查询条件过于复杂：如果你在查询中使用了大量的过滤条件、聚合操作或其他复杂的逻辑，可能会导致查询复杂度超过限制。

  2. 数据量过大：如果你查询的数据量非常大，SkyWalking 在计算查询复杂度时可能会认为这个查询过于复杂。

  3. 查询频率过高：如果你在短时间内频繁执行复杂的查询，可能会导致系统资源紧张，从而触发这个错误。

解决问题

编辑配置文件

vim application.yml

将查询复杂度上限调整为 5000

maxQueryComplexity: ${SW_QUERY_MAX_QUERY_COMPLEXITY:3000}

重启服务

OK了

相关文章：

【skywalking】maximum query complexity exceeded 3336 ＞ 3000

问题 skywalking相关版本信息 jdk：17skywalking：10.1.0apache-skywalking-java-agent：9.3.0ElasticSearch : 8.8.2 问题描述 maximum query complexity exceeded 3336 > 3000 最大查询复杂度超过3336>3000 可能原因 查询条件过于复…...

编程日记 2024/10/30 8:07:11

开源一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码

大家好，我是一颗甜苞谷，今天分享一个开发的聊天应用与AI开发框架，集成 ChatGPT，支持私有部署的源码。 介绍 当前系统集成了ChatGPT的聊天应用，不仅提供了基本的即时通讯功能，还引入了先进的AI技术&#x…...

编程日记 2024/10/30 8:06:10

开发了一个成人学位英语助考微信小程序

微信小程序名称：石榴英语 全称：石榴英语真题助手 功能定位 北京成人学士学位英语辅助学习工具，包含记高频单词，高频词组，专项练习，模拟考试等功能。 开发背景 个人工作需要提高学习英文水平&#xff…...

编程日记 2024/10/30 8:05:09

LeetCode16:最接近的三数之和

原题地址：. - 力扣（LeetCode） 题目描述 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例 1&#xf…...

编程日记 2024/10/30 8:02:06

VisualStudio2022配置2D图形库SFML

文章目录 1. 下载安装SFML库2. 创建C项目并配置SFML配置include目录和库目录链接SFML库配置动态链接库 3. 测试 1. 下载安装SFML库 SFML（Simple and Fast Multimedia Library）C库，适合2D游戏和图形界面，提供了以下模块&#xff1…...

编程日记 2024/10/30 8:00:05

「Mac畅玩鸿蒙与硬件4」鸿蒙开发环境配置篇4 - DevEco Studio 高效使用技巧

本篇将进一步介绍如何在 DevEco Studio 中高效使用各种功能，通过掌握快捷键、代码补全、调试工具等，帮助开发者在鸿蒙应用开发中大幅提升工作效率。 关键词 DevEco Studio快捷键代码补全调试工具项目导航 一、快捷键与高效操作 快捷键是提升开发效率的…...

编程日记 2024/10/30 7:59:03

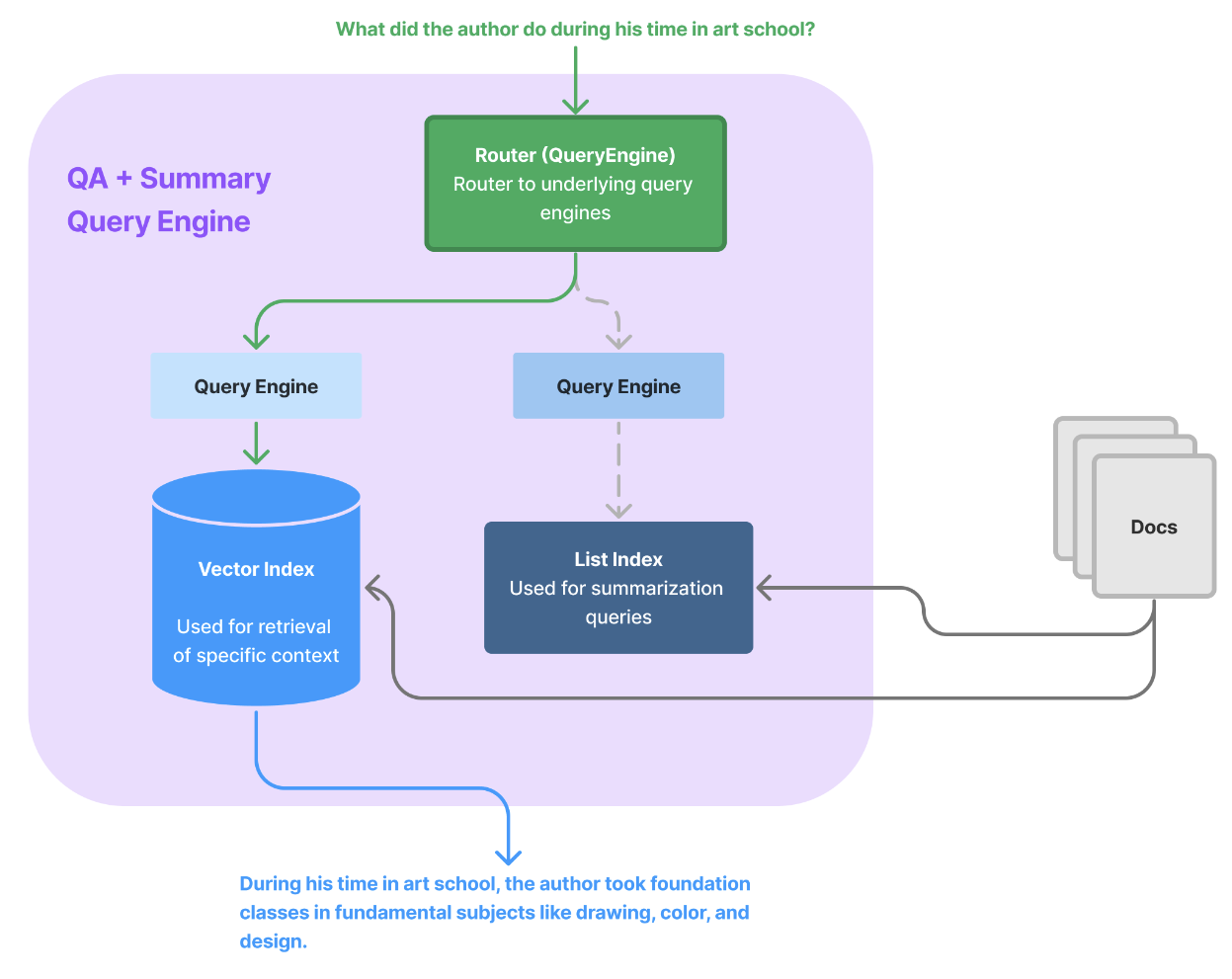
构建生产级的 RAG 系统

对 RAG 应用程序进行原型设计很容易，但要使其高性能、健壮且可扩展到大型知识语料库却很困难。 本指南包含各种提示和技巧，以提高 RAG 工作流程的性能。我们首先概述一些通用技术 - 它们按照简单到复杂的顺序进行排列。然后，我们将更深入地研…...

编程日记 2024/10/30 7:52:57

完全透彻了解一个asp.net core MVC项目模板2

这是《完全透彻了解一个asp.net core MVC项目模板》的第二篇，如果你直接进入了本篇博文而不知道上下文，请先阅读《完全透彻了解一个asp.net core MVC项目模板》的第一篇。 文章目录 一、补充几个问题1、有关导航链接和Tag Helper2、_ViewStart.cshtml与…...

编程日记 2024/10/30 7:45:50

uniapp 如何调用音频

uniapp调用音频 button点击 <view><button click"startPlay">开始播放</button></view>方法实现 startPlay() { const innerAudioContext uni.createInnerAudioContext();innerAudioContext.src /static/sounds/oqc.mp3;innerAudioContex…...

编程日记 2024/10/30 7:44:49

在Facebook运营中使用住宅IP的重要性

在当前社交媒体的浪潮中&#xff0c;Facebook作为全球最大的社交网络之一&#xff0c;吸引了数以亿计的用户。为了在这一平台上实现有效的运营和推广&#xff0c;越来越多的博主和营销人员正在寻求最佳的养号策略。其中&#xff0c;IP地址的选择显得尤为重要&#xff0c;尤其是…...

编程日记 2024/10/30 7:40:46

EJB项目如何升级SpringCloud

记录某金融机构老项目重构升级为微服务过程1 如何从EJB架构拆分微服务 这个非常有趣的过程&#xff0c;整个过程耗时大致接近半年时光&#xff0c;需要考虑到重构升级保留原来的业务线&#xff0c;而且还要考虑后续的维护成本&#xff0c;保留现有的数据库表结构&#xff0c;…...

编程日记 2024/10/30 7:39:45

HTTPS 协议原理

一.HTTPS的定义 大家在刚开始学习的时候是不是也是非常好奇HTTP与HTTPS之间有什么区别和联系&#xff0c;两者都是应用层协议&#xff0c;而HTTPS是在HTTP的基础上引入了加密层&#xff0c;从而将HTTP的明文传输进行加密&#xff0c;保障数据的安全性 二.加密与解密 定义&#…...

编程日记 2024/10/30 7:29:32

Vxe UI 表格行编辑(默认不显示编辑框,点击后可编辑)

效果: HTML代码:(type"integer"为这个,是限制只能输入正整数或负整数,英文和汉字自动转成0) <vxe-tableshow-overflowkeep-sourcev-loading"loading":data"ruleList"ref"Table":row-config"{isHover: true}"height"…...

编程日记 2024/10/30 7:28:31

移远通信闪耀2024香港秋灯展，以丰富的Matter产品及方案推动智能家居产业发展

10月27-30日&#xff0c;2024香港国际秋季灯饰展在香港会议展览中心盛大开展。 作为全球领先的物联网整体解决方案供应商&#xff0c;移远通信再次亮相&#xff0c;并重点展示了旗下支持Matter协议以及亚马逊ACK ( Alexa Connect Kit ) SDK for Matter方案的Wi-Fi模组、低功耗蓝…...

编程日记 2024/10/30 7:27:30

爬虫利器playwright

是什么 它是微软在 2020 年初开源的新一代自动化测试工具&#xff0c;其功能和 selenium 类似&#xff0c;都可以驱动浏览器进行各种自动化操作。还可以录制脚本 案列-01 运行之后我们用它自动打开的谷歌浏览器&#xff0c;打开百度&#xff0c;输入漂亮小姐姐并查找&#x…...

编程日记 2024/10/30 7:26:30

着色器的认识

知识了解&#xff1a; 着色器&#xff1a; 顶点着色器: 用来描述顶点的特性,如位置、颜色等&#xff0c;其中&#xff0c;顶点&#xff1a;是指二维或三维空间中的一个点比如交点或者端点。 片元着色器&#xff1a;用来进行逐片元处理操作&#xff0c;比如光照、颜色叠加等&…...

编程日记 2024/10/30 7:24:28

科技的成就（六十四）

591、《传奇》开始公开测试 "2001 年 9 月&#xff0c;《传奇》开始公开测试。《传奇》&#xff08;全称《热血传奇》&#xff09;是由韩国 WeMade 娱乐开发制作的大型多人在线角色扮演游戏&#xff0c;由 Delphi 编写。盛大网络于2001 年获得该游戏在中国的代理权。《传奇…...

编程日记 2024/10/30 7:23:27

银行信贷风控专题：Python、R 语言机器学习数据挖掘应用实例合集：xgboost、决策树、随机森林、贝叶斯等...

全文链接&#xff1a;https://tecdat.cn/?p38026 分析师&#xff1a;Fanghui Shao 在当今金融领域&#xff0c;风险管控至关重要。无论是汽车贷款违约预测、银行挖掘潜在贷款客户&#xff0c;还是信贷风控模型的构建&#xff0c;以及基于决策树的银行信贷风险预警&#xff0c;…...

编程日记 2024/10/30 7:22:25

〈壮志凌云：独行侠〉中的超高音速战机

电影《壮志凌云&#xff1a;独行侠》中使用的黑星&#xff08;Darkstar&#xff09;高超音速概念战机模型&#xff0c;虽然看起来像是科幻电影里的产物&#xff0c;但这架飞机实际上是由洛克希德马丁公司的臭鼬工厂&#xff08;Skunk Works&#xff09;设计&#xff0c;这是一家…...

编程日记 2024/10/30 7:21:23

k8s集群 ceph rbd 存储动态扩容

k8s 集群 rbd 扩容有两种方法&#xff0c;如下所示 通过StorageClass自动扩容 # kubectl get sc csi-rbd-sc -oyaml|grep allowVolumeExpansion allowVolumeExpansion: true如果搜索有如上字段&#xff0c;说明是可以自动扩容的&#xff0c;修改对应要扩容的 PVC容量&#xf…...

编程日记 2024/10/30 7:20:21

浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）

✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义&#xff08;Task Definition&…...

编程新知 2026/2/8 15:03:14

css实现圆环展示百分比，根据值动态展示所占比例

代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

编程新知 2026/2/5 4:28:28

Redis相关知识总结（缓存雪崩，缓存穿透，缓存击穿，Redis实现分布式锁，如何保持数据库和缓存一致）

文章目录 1.什么是Redis&#xff1f;2.为什么要使用redis作为mysql的缓存&#xff1f;3.什么是缓存雪崩、缓存穿透、缓存击穿&#xff1f;3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

编程新知 2026/2/8 12:24:34

什么是库存周转？如何用进销存系统提高库存周转率？

你可能听说过这样一句话&#xff1a; “利润不是赚出来的&#xff0c;是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业&#xff0c;很多企业看着销售不错&#xff0c;账上却没钱、利润也不见了&#xff0c;一翻库存才发现&#xff1a; 一堆卖不动的旧货…...

编程新知 2026/1/26 13:21:10

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2026/2/7 10:59:19

剑指offer20_链表中环的入口节点

链表中环的入口节点 给定一个链表&#xff0c;若其中包含环&#xff0c;则输出环的入口节点。 若其中不包含环&#xff0c;则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

编程新知 2026/1/31 6:09:22

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表

1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...

编程新知 2026/2/7 8:45:41

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/8/9 0:31:20

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

NFT模式：数字资产确权与链游经济系统构建

NFT模式&#xff1a;数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新&#xff1a;构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议&#xff1a;基于LayerZero协议实现以太坊、Solana等公链资产互通&#xff0c;通过零知…...

编程新知 2026/1/31 23:23:23