rnn/lstm
tip:本人比较小白,看到july大佬的文章受益匪浅,现在其文章基础上加上自己的归纳、理解,以及gpt的答疑,如果有侵权会删。 july大佬文章来源:如何从RNN起步,一步一步通俗理解LSTM_rnn lstm-CSDN博客
-------------------------------------------------------------------------------------------------------------------
1.RNN
1.1 从单层网络到经典的RNN结构
在学习LSTM之前,得先学习RNN,而在学习RNN之前,首先要了解一下最基本的单层网络,它的结构如下图所示:

输入是x,经过变换Wx+b和激活函数f,得到输出y。相信大家对这个已经非常熟悉了。
在实际应用中,我们还会遇到很多序列形的数据:

如:
1. 自然语言处理问题。x1可以看做是第一个单词,x2可以看做是第二个单词,依次类推
2. 语音处理。此时,x1、x2、x3……是每帧的声音信号。
3. 时间序列问题。例如每天的股票价格等等
而其中,序列形的数据就不太好用原始的神经网络处理了。
为了建模序列问题,RNN引入了隐状态h(hidden state)的概念,隐状态h可以对序列形的数据提取特征,接着再转换为输出。
--------------------------------------------------------------------------------------------------------------------
1.2 由x到h
先从h的计算开始看:

图示中记号的含义是:
- a)圆圈或方块表示的是向量。
- b)一个箭头就表示对该向量做一次变换。如上图中
 和
和 分别有一个箭头连接,就表示对
分别有一个箭头连接,就表示对 和
和 各做了一次变换
各做了一次变换
说白了,基于上一个隐藏层的状态
 和当前的输入
和当前的输入 计算得来,且提前说一嘴,泛化到任一时刻,便是
计算得来,且提前说一嘴,泛化到任一时刻,便是,而这里的
一般是tanh、sigmoid、ReLU等非线性的激活函数。
且在实践中,
一般只包含前面若干步而非之前所有步的隐藏状态
在 RNN 模型(或者神经网络模型)中,权重矩阵W和偏置向量 b初始时一般是随机生成的。(在之后不断训练)
(即上面的U、W、b参数)
- 在计算时,每一步使用的参数U、W、b都是一样的,也就是说每个步骤的参数都是共享的,这是RNN的重要特点,一定要牢记;
- 而下文马上要看到的LSTM中的权值则不共享,因为它是在两个不同的向量中。而RNN的权值为何共享呢?很简单,因为RNN的权值是在同一个向量中,只是不同时刻而已。

依次计算剩下来的(使用相同的参数U、W、b):

我们这里为了方便起见,只画出序列长度为4的情况,实际上,这个计算过程可以无限地持续下去。
------------------------------------------------------------------------------------------------------------------------------
1.3 tip: 为什么要用到激活函数?
如果没有激活函数,那么公式就是一个线性映射:
![]()
对于序列数据的多个时间步,如果在每一层计算时都没有激活函数,输出将是输入的线性组合。最终,整个 RNN 变成一个线性模型,即:
![]()
这里的W是个向量。
这是一个简单的线性变换,无法捕捉复杂的非线性关系,而我们通常需要通过神经网络处理非线性问题。
- 序列数据(如自然语言、时间序列)中的依赖关系往往是复杂且非线性的。激活函数(如 Tanh 或 ReLU)能够让神经网络捕捉这些非线性模式,使得模型能够学习复杂的时间依赖关系。
- Tanh 或 Sigmoid 是常见的激活函数,用于控制隐藏状态的更新。Tanh 的输出范围是 [-1, 1],能够有效捕捉输入数据的正负变化;Sigmoid 的输出范围是[0,1],适合用于门控机制。
---------------------------------------------------------------------------------------------------------------------------------
1.4 由h到y
我们目前的RNN还没有输出,得到输出值的方法就是直接通过h进行计算。

这里从h到y又有不同的说法了,即是否也选择激活函数,比如上面出现了softmax函数。
在 RNN 的每一个时间步t,我们有一个隐藏状态 ht,它保存了当前时间步的特征表示。在这个时间步中,我们希望将隐藏状态映射为一个输出 yt。
- 分类任务:预测某个类别(如情感分析)。
- 回归任务:预测数值(如股价、温度)。
- 语言模型:预测下一个单词。
核心公式如下:
![]()
根据任务的不同,我们会选择不同的激活函数f:
-
分类任务(如多分类的文本分类):
使用 Softmax 激活函数,将输出变为概率分布。

其中![]() 。Softmax 确保所有输出值都在 0 到 1之间,并且所有类别的概率和为 1。
。Softmax 确保所有输出值都在 0 到 1之间,并且所有类别的概率和为 1。
举个例子:

2. 二分类任务(如情感分析:积极 vs 消极):
使用 Sigmoid 激活函数,将输出限制在 0 到 1 之间,表示属于某一类别的概率。

3. 回归任务(如股价预测、温度预测):
不需要激活函数,直接使用线性输出:
![]()
----------------------------------------------------------------------------------------------------------------------
1.5 RNN 的正向传播
这里先从x到h,再从h到y,总体来看是x到y,这个步骤就是rnn的正向传播。
而总的来说,在 RNN 中输入和输出的序列长度不需要相同。具体情况要看任务需求,可以是一对一、多对多、一对多 或 多对一 等多种形式。每一种模式都有其适用的场景和特点。
除了刚才图上面的多对多相互对应的情况(相当于即时反馈),还有其他常见的场景。比如下面一对多和多对一:

以及序列长度不同的多对多:

1.6 RNN 的训练:反向传播算法
RNN 的训练与普通神经网络类似,也是通过梯度下降法来优化参数。但由于 RNN 的参数在每个时间步共享,因此要用一种特殊的算法,叫做 BPTT(Backpropagation Through Time,时间反向传播算法)。

上面的W是向量。反向传播和正向传播是对应的,正向传播从头到尾得到返回值y,反向传播则从末尾到开头连续修正相应参数。
---------------------------------------------------------------------------------------------------------------------------
1.7 正向与反向传播的关系
- 单次正向传播:给定一个输入序列 x1,x2,…,xT,RNN 会从第一个时间步传递到最后一个时间步,得到输出序列 y1,y2,…,yT和损失值。
- 单次反向传播(BPTT):从损失函数开始,从时间步 T 向前传播误差,依次传递回到时间步 1。这会更新每一层的参数。
整个训练过程中:RNN 需要多轮(epoch)训练,即对整个数据集多次进行正向和反向传播。
--------------------------------------------------------------------------------------------------------------------------
1.8 RNN 中的梯度消失与梯度爆炸问题
1. 梯度消失问题:
- 在反向传播(BPTT)过程中,误差需要沿时间轴逐步传播。由于每次传播都会涉及到链式求导,当激活函数(如 sigmoid 或 tanh)将输出限制在(0,1) 或 (−1,1)范围内时,梯度的值会越来越小。
- 经过多次时间步的传播后,远处时间步的梯度会指数级缩小,导致模型在更新参数时,无法有效调整靠前时间步的权重。这就是梯度消失。
2. 梯度爆炸问题:
- 这是指在某些情况下,梯度的值会变得非常大,导致模型参数更新不稳定甚至发散。
- 梯度爆炸通常出现在训练初期或权重初始化不当的情况下,但这不是图中所描述问题的主要原因。
解决方案:
- 梯度裁剪(Gradient Clipping):将梯度限制在一个最大值范围内,防止梯度爆炸。
- LSTM / GRU:引入门控机制来解决梯度消失问题。
梯度消失在实际例子上的体现(前部序列信息权重降低):
在 RNN 中,隐藏状态ht会从前一时刻 ht-1 传递到下一时刻 ht+1。这种逐步传播的特点使得距离较远的时间步(例如 x1对应的状态)信息可能会在后面的时间步中变得越来越不重要。


梯度爆炸的例子倒是挺少见,反正就是梯度消失的相反面,由于某些不好的原因导致的梯度过于大,导致模型参数更新不稳定甚至发散。
2. LSTM
2.1 为什么要从rnn到lstm(解决梯度消失和梯度爆炸)
LSTM 通过引入细胞状态和门控机制(遗忘门、输入门和输出门),实现了信息的线性传递,避免了多次非线性激活导致的梯度消失。同时,遗忘门动态调节信息的保留与遗忘,避免无关信息的累积,减少梯度爆炸的风险。这种设计使得梯度在长时间步上传递时更加稳定,从而有效解决了 RNN 中的梯度消失和梯度爆炸问题,让模型能够捕捉长期依赖关系。
再具体一点:
LSTM 通过以下方式解决了 RNN 中的梯度消失和梯度爆炸问题:
- 细胞状态的线性传递:信息可以跨多个时间步不受抑制地传递,缓解了梯度消失问题。
- 门控机制的动态调节:输入门、遗忘门、输出门选择性地更新状态,避免了无关信息的累积,减少了梯度爆炸的风险。
- 减少梯度缩放的次数:LSTM 通过线性更新状态,将非线性变换限制在局部,使梯度的稳定性更好。
- 遗忘门控制信息流:有效控制长期状态中的冗余信息,进一步缓解梯度爆炸问题。
---------------------------------------------------------------------------------------------------------------------------------
2.2 忘记门--Forget Gate(ft)
内容来自如何从RNN起步,一步一步通俗理解LSTM_rnn lstm-CSDN博客
可以点进网页里看动图,支持原作者july。
2.3 输入门--Input Gate(it)and 候选状态--Candidate State(~Ct)
2.4 细胞状态--Cell State(Ct)

2.5 输出门--Output Gate(ot)

2.6 数据形状(向量、矩阵等)
上面提到的公式中大部分符号(如xt、ht、Ct等)都代表向量或矩阵,而不是标量。这是因为 LSTM 和 RNN 处理的是高维数据,如词向量、时间序列中的多特征数据等。


其中,batch_size 表示一个批次中的样本数量,hidden_size 是隐藏状态的维度。

2.7 提到的权值是否共享问题
在遗忘门部分,july哥提到的rnn和lstm权值是否共享问题,其实很容易理解,rnn和lstm在不同时间步之间都是共享的,而在lstm不同门里,不同门有独立的参数。
- RNN 中:所有时间步的参数共享,即所有时间步使用相同的权重矩阵 W,U。
- LSTM 中:不同的门(遗忘门、输入门、输出门、候选单元)之间的权重不共享,但在同一门的不同时间步之间权重是共享的。
2.8 激活函数(sigmoid 或 tanh)的选择
- sigmoid 用于比例控制(信息保留、写入、输出),因为其输出在0−1 之间。
- tanh 用于状态表示(候选状态和隐藏状态),因为其输出在 −1 到 1之间,允许正负信息的存在。
通过这种组合,LSTM 能够精确控制信息的流动,避免梯度消失,并有效捕捉长时间依赖关系。
具体机制大致如下:






2.9 lstm的参数调整(反向传播)
lstm也是通过反向传播来调节参数,先介绍下在调参层面上lstm和rnn之间的关系。
LSTM 和 RNN 在反向传播中主要区别和联系是:
- RNN 由于简单且高效,适合处理 短序列或短期依赖问题。但它的梯度消失问题使得它难以捕捉长时间的依赖关系。
- LSTM 通过 细胞状态的线性传递和门控机制 缓解了梯度消失问题,因此更适合处理 长时间序列。但代价是训练时的计算量更大,参数更新更复杂。
lstm调参在大方向上类似于rnn,先正向传播,后计算损失。

然后是反向传播调参,即把损失函数对各参数求偏导(梯度)

然后结合旧的参数和学习率,得到新的参数,此外还提到了一些优化算法,能更好的调整学习率。

最后,有一些超参数调节。

相关文章:

rnn/lstm
tip:本人比较小白,看到july大佬的文章受益匪浅,现在其文章基础上加上自己的归纳、理解,以及gpt的答疑,如果有侵权会删。 july大佬文章来源:如何从RNN起步,一步一步通俗理解LSTM_rnn lstm-CSDN博…...
袋鼠云产品功能更新报告12期|让数据资产管理更高效
本期,我们更新和优化了数据资产平台相关功能,为您提供更高效的产品能力。以下为第12期袋鼠云产品功能更新报告,请继续阅读。 一、【元数据】重点更新 |01 元数据管理优化,支持配置表生命周期 之前系统中缺少一个可以…...

MATLAB——入门知识
内容源于b站清风数学建模 目录 1.帮助文档 2.注释 3.特殊字符 4.设置MATLAB数值显示格式 4.1.临时更改 4.2.永久改 5.常用函数 6.易错点 1.帮助文档 doc sum help sum edit sum 2.注释 ctrl R/T 3.特殊字符 4.设置MATLAB数值显示格式 4.1.临时更改 format lon…...

C#从零开始学习(用户界面)(unity Lab4)
这是书本中第四个unity Lab 在这次实验中,将学习如何搭建一个开始界面 分数系统 点击球,会增加分数 public void ClickOnBall(){Score;}在OneBallBehaviour类添加下列方法 void OnMouseDown(){GameController controller Camera.main.GetComponent<GameController>();…...

Axure PR 9 多级下拉清除选择器 设计交互
大家好,我是大明同学。 Axure选择器是一种在交互设计中常用的组件,这期内容,我们来探讨Axure中选择器设计与交互技巧。 OK,这期内容正式开始 下拉列表选择输入框元件 创建选择输入框所需的元件 1.在元件库中拖出一个矩形元件。…...

分布式项目pom配置
1. 父项目打包方式为 pom <packaging>pom</packaging> 2. 父项目版本配置 <properties><maven.compiler.source>17</maven.compiler.source><maven.compiler.target>17</maven.compiler.target><project.build.sourceEncod…...

2. Flink快速上手
文章目录 1. 环境准备1.1 系统环境1.2 安装配置Java 8和Scala 2.121.3 使用集成开发环境IntelliJ IDEA1.4 安装插件2. 创建项目2.1 创建工程2.1.1 创建Maven项目2.1.2 设置项目基本信息2.1.3 生成项目基本框架2.2 添加项目依赖2.2.1 添加Flink相关依赖2.2.2 添加slf4j-nop依赖2…...
Java-I/O框架06:常见字符编码、字符流抽象类
视频链接:16.16 字符流抽象类_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Tz4y1X7H7?spm_id_from333.788.videopod.episodes&vd_sourceb5775c3a4ea16a5306db9c7c1c1486b5&p16 1.常见字符编码 IOS-8859-1收录了除ASCII外,还包括西欧…...
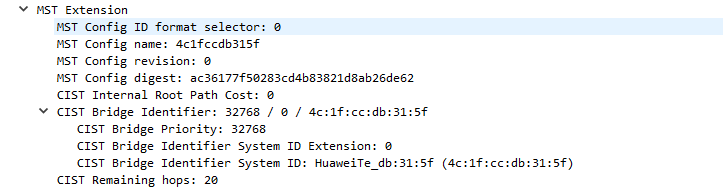
计算机网络-MSTP的基础概念
前面我们大致了解了MSTP的由来,是为了解决STP/RSTP只有一根生成树导致的VLAN流量负载分担与次优路径问题,了解MSTP采用实例映射VLAN的方式实现多实例生成树,MSTP有很多的理论概念需要知道,其实与其它的知识一样理论复杂配置还好的…...

P1037 [NOIP2002 普及组] 产生数
[NOIP2002 普及组] 产生数 题目描述 给出一个整数 n n n 和 k k k 个变换规则。 规则: 一位数可变换成另一个一位数。规则的右部不能为零。 例如: n 234 , k 2 n234,k2 n234,k2。有以下两个规则: 2 ⟶ 5 2\longrightarrow 5 2⟶5。 …...

【分布式知识】分布式对象存储组件-Minio
文章目录 什么是minio核心特点:使用场景:开发者工具:社区和支持: 核心概念什么是对象存储?MinIO 如何确定对对象的访问权限?我可以在存储桶内按文件夹结构组织对象吗?如何备份和恢复 MinIO 上的…...

跨平台开发支付组件,实现支付宝支付
效果图: custom-payment : 在生成预付订单之后页面中需要弹出一个弹层,弹层中展示的内容为支付方式(渠道),由用户选择一种支付方式进行支付。 该弹层组件是以扩展组件 uni-popup 为核心的,关于…...

API 接口:为电商行业高效发展注入强劲动力
一、动力之源:API 接口在电商中的角色剖析 在电商行业的广袤版图中,API 接口宛如一台强劲的发动机,是推动其高效发展的核心动力来源。它不再仅仅是一个技术工具,而是成为了连接电商各个环节的 “神经系统”,使得信息、…...

Golang的跨平台开发
Golang的跨平台开发 一、Golang跨平台开发概述 语言是一种开源的编程语言,由Google开发,广泛应用于云计算和网络编程领域。Golang具有并发性好、性能优异、内存管理自动化等特点,因此备受开发者青睐。其中,Golang的跨平台特性使得…...

txt数据转为pdf格式并使用base64解密输出
使用该方法请注意:因为此方法使用了base64解密,需要保证txt中的数据首先用了base64加密,如果只是普通的二进制数据,该方法并不适用 第一步 <dependency><groupId>org.apache.pdfbox</groupId><artifactId&…...

鸿蒙开发-状态+判断+循环
🌈个人主页:前端青山 🔥系列专栏:鸿蒙开发篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来鸿蒙开发篇专栏内容:鸿蒙开发-状态判断循环 目录 1.状态1原始类型 2.引用类型 2.判断 3.循环 1.基本使用…...
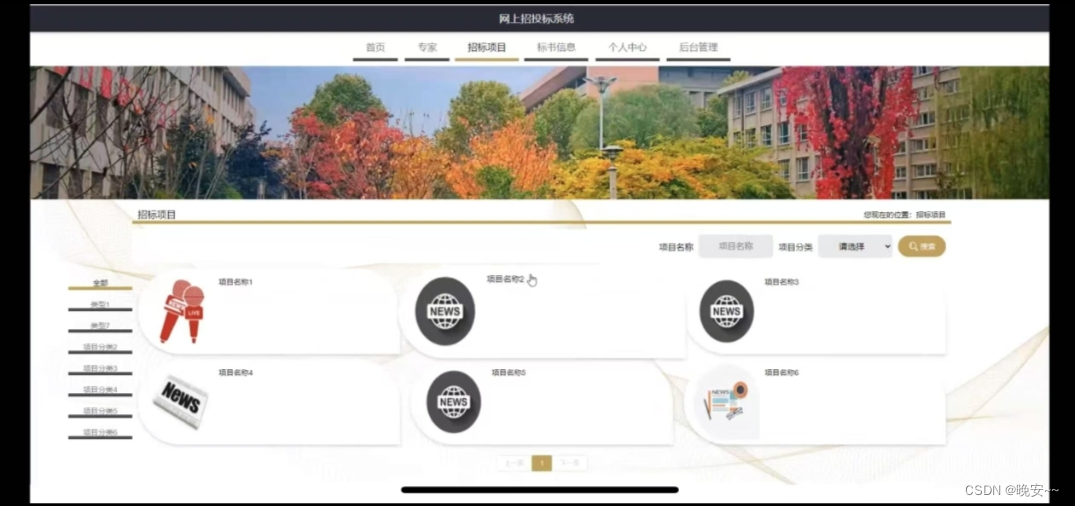
基于SSM网上招投标管理系统的设计
管理员账户功能包括:系统首页,个人中心,用户管理,招标者管理,专家管理,项目分类管理,招标项目管理,系统管理 前台账号功能包括:系统首页,个人中心࿰…...

「C/C++」C++ 设计模式 之 单例模式(Singleton)
✨博客主页何曾参静谧的博客📌文章专栏「C/C」C/C程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasoli…...

WPF的行为(Behavior)
WPF(Windows Presentation Foundation)是微软.NET框架中用于构建Windows客户端应用程序的UI框架。它提供了一种声明性的方式来定义用户界面,并且支持MVVM(Model-View-ViewModel)设计模式。 在WPF中,“行为…...

SpringBoot框架:闲一品交易平台的新突破
摘 要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,闲一品交易平台当然也不能排除在外。闲一品交易平台是以实际运用为开发背景,运用软件工程原理和开发方法&…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...
)
零基础在实践中学习网络安全-皮卡丘靶场(第十一期-目录遍历模块)
经过前面几期的内容我们学习了很多网络安全的知识,而这期内容就涉及到了前面的第六期-RCE模块,第七期-File inclusion模块,第八期-Unsafe Filedownload模块。 什么是"遍历"呢:对学过一些开发语言的朋友来说应该知道&…...
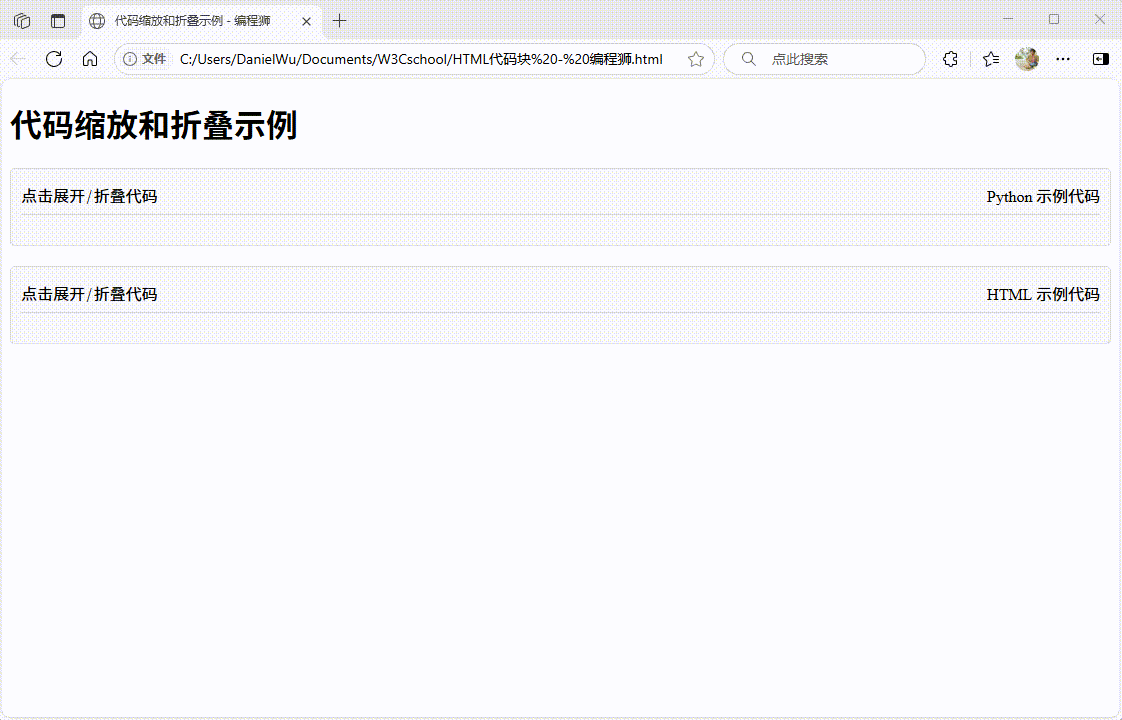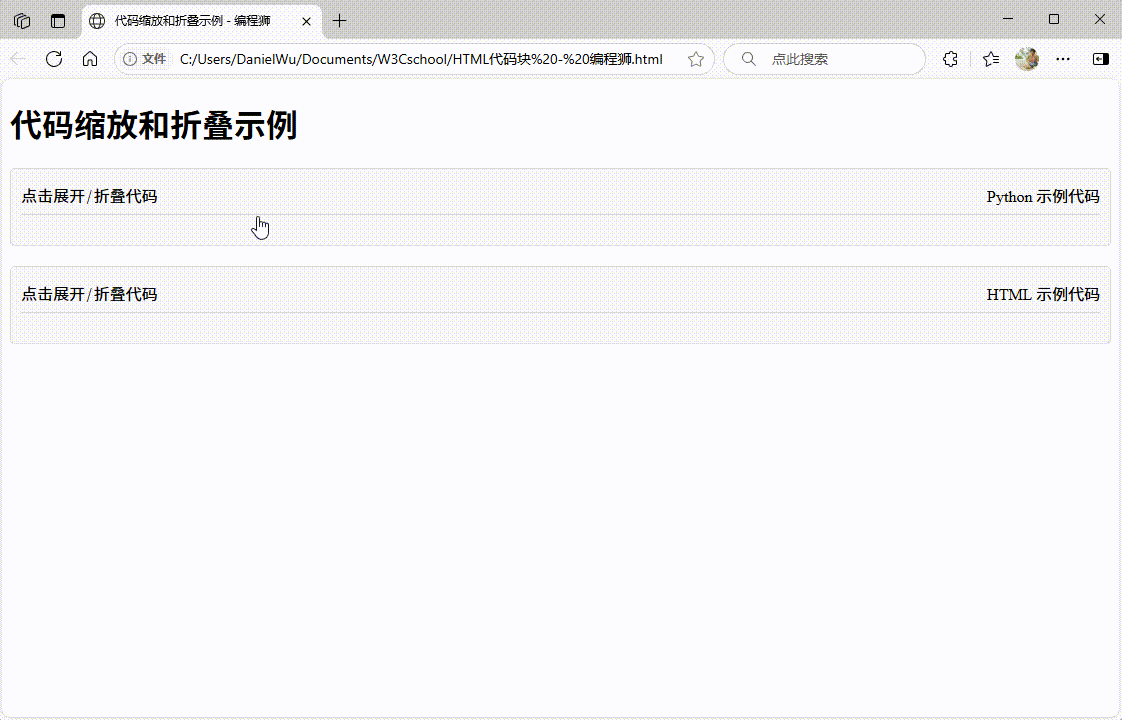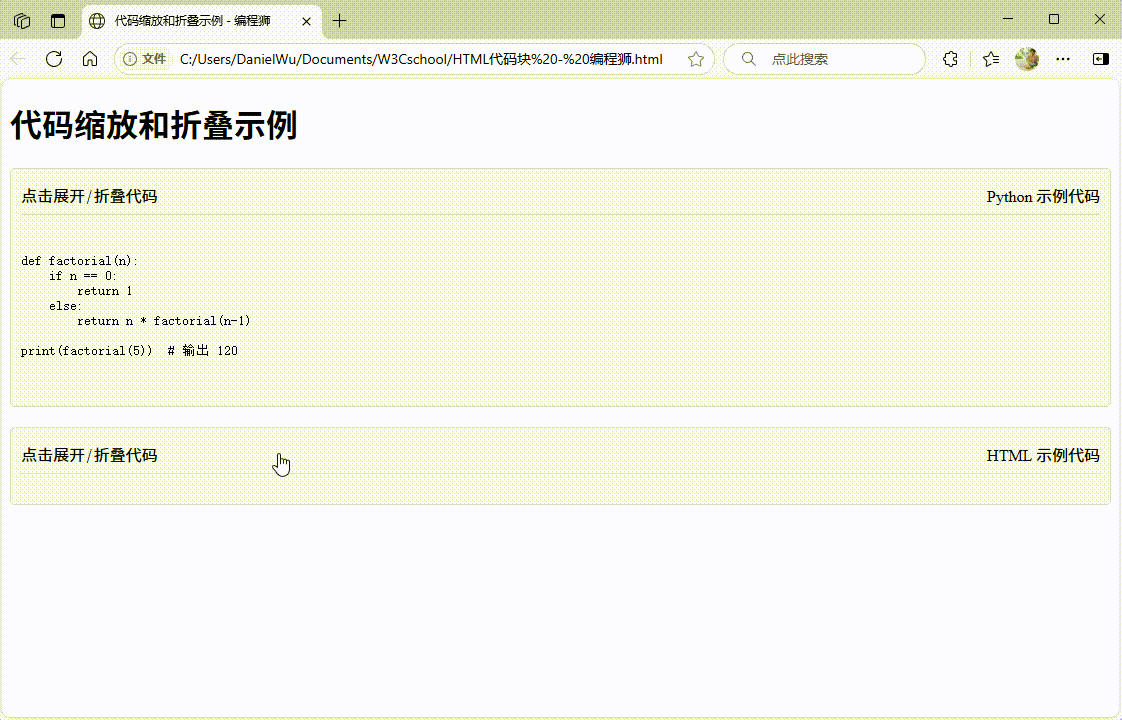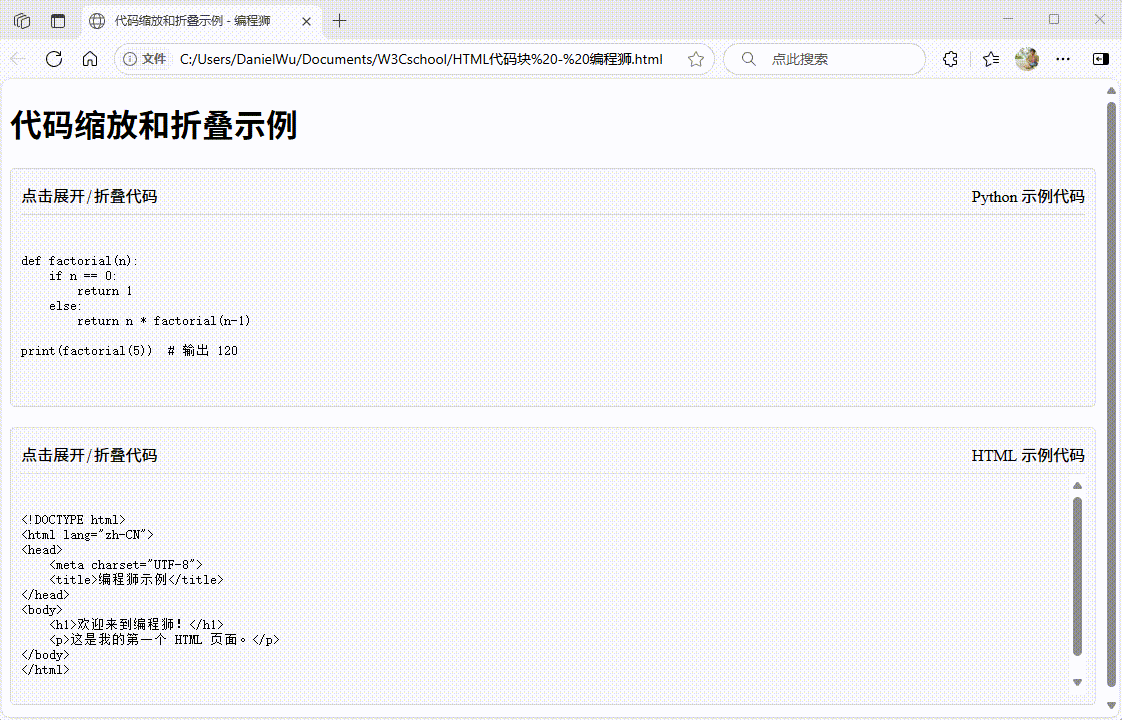
如何用 HTML 展示计算机代码
原文:如何用 HTML 展示计算机代码 | w3cschool笔记 (请勿将文章标记为付费!!!!) 在编程学习和文档编写过程中,清晰地展示代码是一项关键技能。HTML 作为网页开发的基础语言&#x…...
跑通 TrackNet-Badminton-Tracking-tensorflow2 项目全记录
📝 跑通 TrackNet-Badminton-Tracking-tensorflow2 项目全记录 git clone https://github.com/Chang-Chia-Chi/TrackNet-Badminton-Tracking-tensorflow2.git TrackNet-Badminton-Tracking-tensorflow2 conda create --prefix /cloud/TrackNet-Badminton-Tracking-…...

如何安装并使用RustDesk
参考: 搭建 RustDesk Server:打造属于自己的远程控制系统,替代 TeamViewer 和 ToDesk! 向日葵、ToDesk再见!自己动手,自建RustDesk远程服务器真香! 通俗易懂:RustDesk Server的搭…...

