10 最长回文子串、买卖股票的最好时机(一)、[NOIP2002 普及组] 过河卒24_10_30
这里写目录标题
- cpp 10
- 1 最长回文子串
- 1.1 题目
- 1.2 思路
- 1.3 程序实现
- 2 买卖股票的最好时机(一)
- 2.1 题目
- 2.2 思路
- 2.3 程序实现
- 2.4 程序实现 – 优化
- 3 [NOIP2002 普及组] 过河卒
- 3.1题目
- 3.2 思路
- 3.3程序实现 – dp
- 4 题目链接
cpp 10
1 最长回文子串
1.1 题目

1.2 思路
读完了题知道,在一个长度为n的字符串中,求最长回文子串的长度。回文子串可以理解为对称的字符串。因为具有对称性,那么基本思路就是“中心扩展法”,也就是依次字符串,然后遍历到该字符就向其两边扩展,如果两边的字符相等,那么就记录到retlen变量中,遍历完最后得到最大长度返回即可。为了方便理解,画个图:

此外,分析示例,还得注意奇数偶数的区别,那么接下来就是程序实现。
1.3 程序实现
首先,按照思路分析的“中心扩展法”,遍历字符串,且从i处从中心站展开,依次求得的retlen,与retlen不断比较更新,然后又因为需要区分奇数和偶数的情况,所以分别求得最大值,最后再比较依次得到最终最大的retlen返回即可。
class Solution
{
public:int getLongestPalindrome(string A){size_t len = A.size();int left = 0;int right = 0;int retlen = 0;//偶数for(int i = 0;i < len; i++){left = i;right = i + 1;while(left >= 0 && right < len && A[left] == A[right]){left--;right++;}retlen = max(retlen ,right - left - 1);}//奇数for(int j = 0;j < len;j++){left = j;right = j;while(left >= 0 && right < len && A[left] == A[right]){left--;right++;}retlen = max(retlen ,right - left - 1);}return retlen ;}
};
2 买卖股票的最好时机(一)
2.1 题目

2.2 思路
读完题,知道对于一组股票的买卖机制,只能买卖一次,让求得获得的利润的最高收益,如果无论什么时候买入卖出都是亏,不管亏多少,即没有利润则输出0即可。那么,基本思路就是枚举/蛮力法,求得每一组的利润差,返回最大值,尝试过后,发现两层for会超时,此题限制1ms解决。因此,需要在蛮力法基础上优化,所以蛮力法也写一写,然后,基于蛮力法,回溯重复了太多次,进行优化,思考发现,如果我们反过来逆向思维,先考虑卖出的价值,然后,就只需要求得该卖出点之前的最小价值即可,得到的差就是最大差,也就是说只需要遍历一遍即可。接下来就是程序实现。
2.3 程序实现
首先,根据蛮力法思路分析,依次枚举所有情况,求得最大差值输出即可,此题会超时。所以得进行优化。
#include <iostream>
using namespace std;const int N = 1e5 +10;int arr[N];int main()
{int n;cin >> n;for(int i = 0;i < n;i++)cin >> arr[i];int maxval = 0;for(int i = 0;i < n; i++){for(int j = i;j < n;j++){maxval = max(maxval , arr[j]- arr[i]);}}cout << maxval << endl;return 0;
}
2.4 程序实现 – 优化
基于上述的蛮力法,进行优化,为了方遍理解,根据思路分析画个演示图:

那么程序实现,按照要求写好输入,然后定义minval初始化arr[0]当作假设的最小值进行遍历比较更新即可,再定义一个maxSub表示遍历至 i 位置时,与minval的最大差值,值得注意的是,遍历时注意minval和maxSub的顺序性,先求最小值minval再求maxSub即可。
#include <iostream>
#include <vector>
using namespace std;int main()
{int n = 0;cin >> n;vector<int> arr(n);int m = 0;while(n--){cin >> arr[m];m++;}int minval = arr[0];int submax = 0;for(int i = 0;i<arr.size();i++){minval = min(arr[i],minval);submax = max(submax, arr[i] - minval);}cout << submax << endl;return 0;
}
3 [NOIP2002 普及组] 过河卒
3.1题目

3.2 思路
读完题,知道让求从A点按照一定的规则,走到B点最多有多少条的路径。分析题目需要知道,按照一定的规则,可以向右或向下走就想到了动态规划dp思路,然后题目中还需要注意的是,马的控制点不能被走(访问),也就是象棋中马在坐标上走的斜"日"所设计的点,且包括马的起始点都被称为控制点。其中,马是一开始就给出的固定点(x,y),且题目也给了马跳跃点与马起始点的关系。此外,还得注意的是,根据示例和棋盘得知,棋盘的大小是(n+1)(m+1)。
所以,综合所述,思考分析得出:
(1)、可使用动态规划dp思路解题;
(2)、马的控制点,除了斜“日”外,还包括自身的起始位置;
(3)、棋盘的大小是(n+1)(m+1).
所以分析了注意点后,那么就回归到动态规划的dp状态表示和状态转移方程上来;
由题目的走的规则,定义dp[i][j]状态表示:走到该位置最多有几条路径;
推导状态转移方程:dp[i][j] = d[i][j-1] + d[i-1][j] ;
此外注意如果B点起始位置就与马的起始位置或控制点重合,还有就是B点的上方和左方全部被阻塞,即是控制点,那么以上极端情况,此时dp[i][j] = 0; 那么接下来,就是程序实现。
3.3程序实现 – dp
首先,根据思路的分析写好输入,定义开辟好dp数组(两个坑点稍后说),根据棋盘的大小为了坐标能够统一描述所以这里就额外多开辟一行一列,那么x和y就需要映射坐标+=1即可,然后探究dp的初始化问题,画个图更清晰:

接着,实际二维数组就从[1,n+1]和[1,m+1]遍历,不断判断极端情况的处理即可,最后输出dp[n+1][m+1]即可。到此,思路没有问题,总结步骤为一下几点:
(1)、映射x和y的坐标;
(2)、根据(多开辟一层)数组定义初始化dp[0][1] =1 或 dp[1][0] = 1均可;
(3)、遍历二位数组,注意边界控制从[1,n+1]和[1,m+1]遍历;
a、判断极端情况:1.马的控制点阻塞路径 2.重合问题;
b、正常执行状态转移方程:dp[i][j] = d[i][j-1] + d[i-1][j] ;
(4)、最后输出dp[n+1][m+1]即可.
另外,上面提到的两个坑点,在于我写好后,提交不通过,发现,数据超范围了,所以最好使用long long开辟数组,还有一个坑点是在于开辟的大小范围由于多开辟的一层使用,所以这里至少大于等于22才行。之前使用dp[21][21]无法通过所有用例哈。
#include <iostream>
using namespace std;long long dp[22][22];int main()
{int n,m,x,y;cin >> n >> m >> x >> y;//映射坐标x += 1;y += 1;//初始化dp[0][1] = 1;//遍历for(int i = 1;i <= n+1; i++){for(int j = 1;j <= m+1; j++){//极端情况的处理: 1.马控制点 2.自身重合if((i != x && j != y && abs(i - x) + abs(j - y) == 3) || (i == x && j == y)){dp[i][j] = 0;}else{dp[i][j] = dp[i][j-1] + dp[i-1][j];}}}cout << dp[n+1][m+1] << endl;return 0;
}
4 题目链接
最长回文子串
买卖股票的最好时机(一)
[NOIP2002 普及组] 过河卒
相关文章:

10 最长回文子串、买卖股票的最好时机(一)、[NOIP2002 普及组] 过河卒24_10_30
这里写目录标题 cpp 101 最长回文子串1.1 题目1.2 思路1.3 程序实现 2 买卖股票的最好时机(一)2.1 题目2.2 思路2.3 程序实现2.4 程序实现 – 优化 3 [NOIP2002 普及组] 过河卒3.1题目3.2 思路3.3程序实现 – dp 4 题目链接 cpp 10 1 最长回文子串 1.1 题目 1.2 思路 读完了…...

Handler、Looper、message进阶知识
Android Handler、Looper、Message的进阶知识 在Android开发中,Handler、Looper和Message机制是多线程通信的核心。为了深入理解并优化它们的使用,尤其是在高并发和UI性能优化中,可以利用一些高级特性。 1. Handler的高阶知识 Handler在基本…...

一文理解决策树:原理、数学公式与全流程实战讲解
一、背景与来源 决策树(Decision Tree)是一种常见的机器学习算法,主要用于分类和回归问题。其概念来源于统计学和决策论,能够直观地模拟人类的决策过程。最早的决策树算法之一是 1963 年由 Hunt 等人提出的,该算法逐渐…...

day04-LogStash扩展
1.LogStash性能不稳定(某天关闭后,再次启动就非常慢),所以后面我们用Filebeat。2.先禁用 # geoip { # source > "clientip" # }3.在生产中要是用nignx服务或tomcat服务我们用EFK架构就可以排查技巧观察点 LogS…...
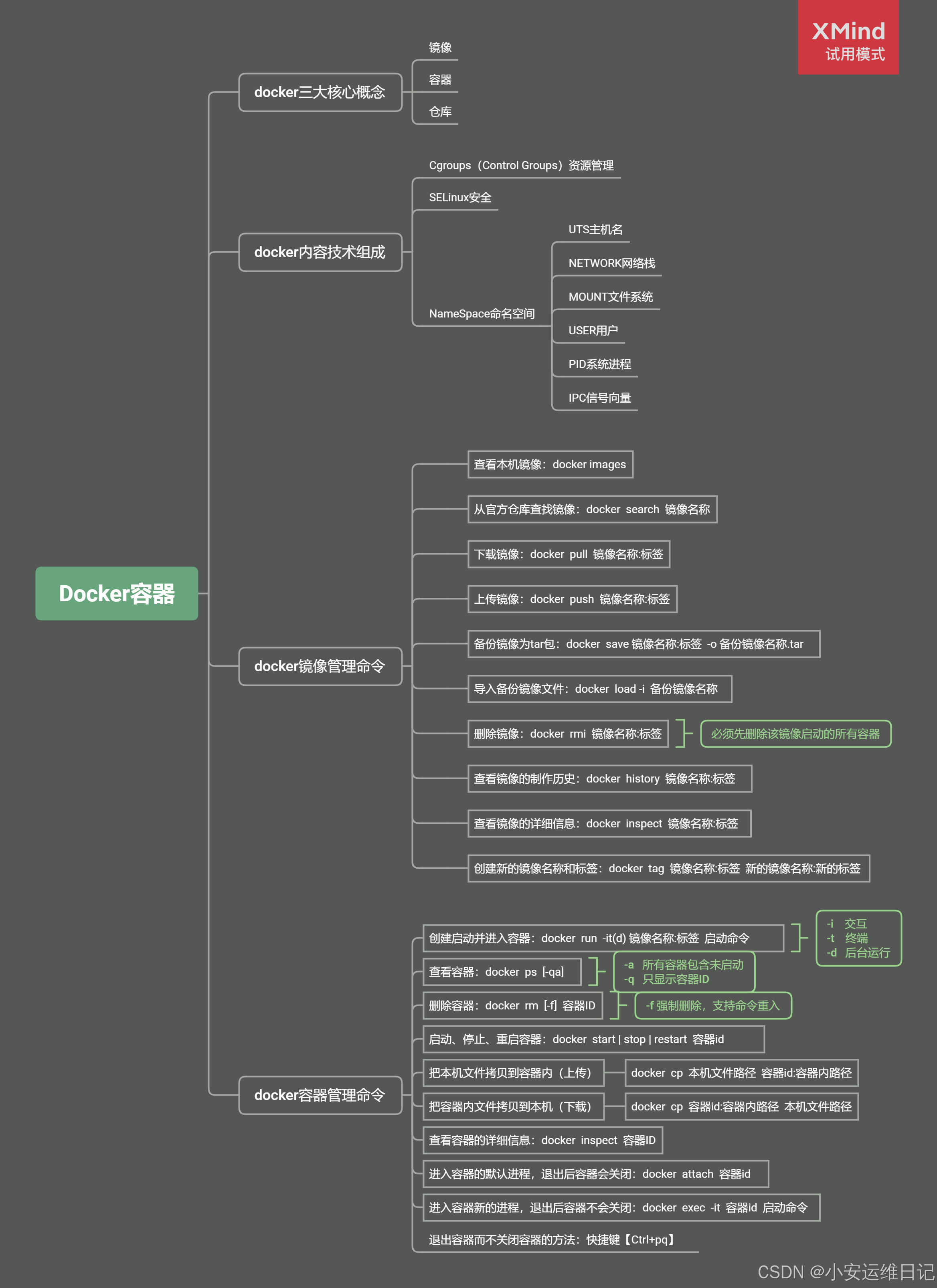
Linux云计算 |【第五阶段】CLOUD-DAY4
主要内容: Linux容器基础、安装Docker、镜像管理、容器管理、容器部署应用 一、容器介绍 容器(Container) 是一种轻量级的虚拟化技术,用于在操作系统级别隔离应用程序及其依赖项。容器允许开发者在同一台主机上运行多个独立的应…...

为什么QNAP威联通NAS的APP center无法安装APP?
创作立场:原创不易,拒绝搬运~ hello大家好,我是你们的老伙伴,稳重的大王~ 如题,大王带你一起来排查一下,可能遇到的问题。如有帮助,请给个关注鼓励,互谢~ 1 首先,安装…...

Kafka 基础入门
文章内容是学习过程中的知识总结,如有纰漏,欢迎指正 文章目录 前言 1. 核心概念 1.1 Producer 1.2 broker 1.3 consumer 1.4 zookeeper 1.5 controller 1.6 Cluster 2. 逻辑组件 2.1 Topic 2.2 Partition 2.3 Replication 2.4 leader & follower 3. …...

网络问题排查
1.ping 域名发现响应时间很长,怎么分析卡在哪里? 当你在 Linux 系统中 ping 一个域名并发现响应时间很长时,可能存在于多个环节的问题。以下是一些步骤和工具,可以帮助你分析和诊断问题出在哪里: 1. 检查 DNS 解析时…...

webGlL变量的声明与使用
抢先观看: 变量的声明格式:<存储限定符><类型限定符><变量名> 存储限定符:const, attribute, uniform, varying, buffer。 类型限定符:void, bool, int, float, double, vec2, vec3, vec4, mat2, mat3, mat4, s…...

qt的c++环境配置和c++基础【正点原子】嵌入式Qt5 C++开发视频
QT c 环境配置和c基础 c环境配置和工程创建 1.配置步骤 2.新建qt 工程目录和工程 3.重启qt后打开最近的qt项目 c基础-类和对象 1.什么是类和对象 A.类的定义 B.类的结构表示 C.类的访问权限 D.对象的定义 E.类和对象的关系 2.类…...

中间件安全(三)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。 前言: 本文主要讲解apache命令执行漏洞(cve_2021_41773)。 靶场链接:Vulfocus 漏洞威胁分析平台 一,漏洞简介。 cve_2021_41773漏洞…...

唱戏机上的内存卡怎么加密?教你两个方法
唱戏机是中老年人群休闲时光的好伴侣。然而,很多唱戏机商家都会面临一个困扰:如何保护唱戏机上内存卡中的音频,避免他人随意复制呢?今天这篇文章看完,问题将迎刃而解~ 数据隐藏 将内存卡插到电脑上,对卡里…...
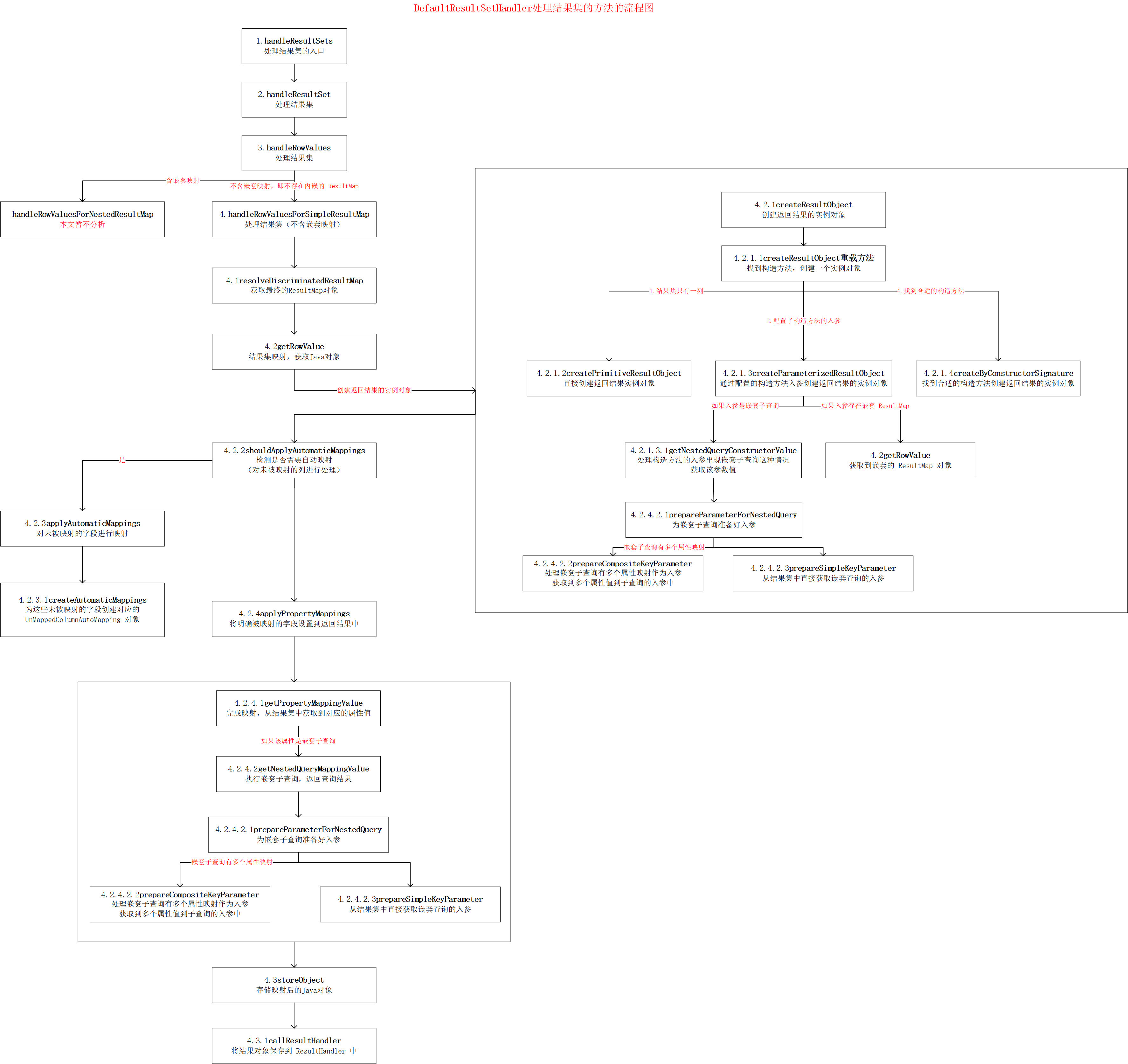
MyBatis 源码分析 - SQL执行过程(三)之 ResultSetHandler
MyBatis的SQL执行过程 在前面一系列的文档中,我已经分析了 MyBatis 的基础支持层以及整个的初始化过程,此时 MyBatis 已经处于就绪状态了,等待使用者发号施令了 那么接下来我们来看看它执行SQL的整个过程,该过程比较复杂ÿ…...

webpack解决使用window.open方法打开history路由页面提示404的问题
问题: 一般情况下应该使用history.push(/ssh)打开history路由页面 但项目中使用window.open(/ssh),然后使用new WebSocket进行通信 开发环境下启动项目后,/ssh页面打开却显示cannot get /ssh,控制台提示404 排查问题: 在React开发环境中使用 window.open 打开路由页面时&a…...

怎么把视频的声音转化为文字免费?7个小妙招,视频转文字轻松解决!
您是否也曾在做会议记录时,希望能免费把视频的声音转化为文字呢?在如今我们的办公生活中,用视频记录会议、记录的生活似乎已经成为了我们一项必备技能,但也并非所有人都能轻松获取视频中的信息。尤其是有着听力障碍的人群…...

【无标题】2024年第五届 MathorCup 数学应用挑战赛——大数据竞赛赛题
2024年第五届 MathorCup 数学应用挑战赛——大数据竞赛赛题已发布~,本届初赛时间为:2024年10月25日18:00至2024年11月1日20:00。本次赛题分为A,B两道,所有参赛队从赛道 A、B 中任选一题作答。在报名系统内选择自己队伍的赛道时&am…...

新能源行业必会基础知识---电力现货问答---第9问---什么是输电权?什么是输电权市场?
新能源行业必会基础知识-----电力现货问答-----主目录-----持续更新https://blog.csdn.net/grd_java/article/details/142909208 虽然这本书已经出来有几年了,现货市场已经产生了一定变化,但是原理还是相通的。还是推荐大家买来这本书进行阅读观看&#…...

视频文案素材获取渠道分享
做视频时为文案发愁?别担心!今天为大家推荐几个实用的视频文案素材网站,让你灵感爆棚,轻松创作文案。 蛙学网 首先要推荐的是蛙学网。作为专业短视频素材库,不仅有修牛蹄、解压视频等热门素材,还为短视频创…...

尚硅谷-react教程-求和案例-数据共享(下篇)-完成数据共享-笔记
#1024程序员节|征文# public/index.html <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>redux</title></head><body><div id"root"></div></body> </html&…...

VB中如何创建和使用自定义控件
在Visual Basic(VB)中,创建和使用自定义控件是一个高级功能,它允许开发者根据特定需求创建具有独特行为和外观的控件。以下是在VB中创建和使用自定义控件的一般步骤: 一、创建自定义控件 打开VB开发环境: …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
