近似线性可分支持向量机的原理推导
近似线性可分的意思是训练集中大部分实例点是线性可分的,只是一些特殊实例点的存在使得这种数据集不适用于直接使用线性可分支持向量机进行处理,但也没有到完全线性不可分的程度。所以近似线性可分支持向量机问题的关键就在于这些少数的特殊点。
相较于线性可分情况下直接的硬间隔最大化策略,近似线性可分问题需要采取一种称为“软间隔最大化”的策略来处理。少数特殊点不满足函数间隔大于1的约束条件,近似线性可分支持向量机的解决方案是对每个这样的特殊实例点引入一个松弛变量 ξ i ⩾ 0 \xi_i \geqslant 0 ξi⩾0 ,使得函数间隔加上松弛变量后大于等于1,约束条件就变为:
y i ( w ⋅ x i + b ) + ξ i ⩾ 1 (9-37) y_i(w \cdot x_i + b) + \xi_i \geqslant 1 \tag{9-37} yi(w⋅xi+b)+ξi⩾1(9-37)
对应的目标函数也变为:
1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 N ξ i (9-38) \frac{1}{2} ||w||^2 + C \sum_{i=1}^{N} \xi_i \tag{9-38} 21∣∣w∣∣2+Ci=1∑Nξi(9-38)
其中 C C C 为惩罚系数,表示对误分类点的惩罚力度。
跟线性可分支持向量机一样,近似线性可分支持向量机可形式化为一个凸二次规划问题:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s.t. y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ≥ 0 , i = 1 , 2 , ⋯ , N (9-39) \begin{aligned} & \min_{w,b,\xi} \quad \frac{1}{2} \| w \|^2 + C \sum_{i=1}^{N} \xi_i \\ & \text { s.t. } \quad y_i (w \cdot x_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \cdots, N \\ & \quad \xi_i \geq 0, \quad i = 1, 2, \cdots, N \tag{9-39} \end{aligned} w,b,ξmin21∥w∥2+Ci=1∑Nξi s.t. yi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N(9-39)
类似于 9.2.1 节的线性可分离支持向量机的凸二次规划问题,我们同样将其转化为对偶问题进行求解。式(9-39)的对偶问题为:
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N (9-40) \begin{aligned} & \min_{\alpha} \quad \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & \quad 0 \leq \alpha_i \leq C, \quad i = 1, 2, \cdots, N \tag{9-40} \end{aligned} αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=00≤αi≤C,i=1,2,⋯,N(9-40)
式(9-39)的拉格朗日函数为:
L ( w , b , ξ , α , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) − ∑ i = 1 N μ i ξ i (9-41) L(w, b, \xi, \alpha, \mu) = \frac{1}{2} \| w \|^2 + C \sum_{i=1}^{N} \xi_i - \sum_{i=1}^{N} \alpha_i (y_i (w \cdot x_i + b) - 1 + \xi_i) - \sum_{i=1}^{N} \mu_i \xi_i \tag{9-41} L(w,b,ξ,α,μ)=21∥w∥2+Ci=1∑Nξi−i=1∑Nαi(yi(w⋅xi+b)−1+ξi)−i=1∑Nμiξi(9-41)
原始问题为极小极大化问题,则对偶问题为极大极小化问题。同样先对 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ) 求 w , b , ξ w, b, \xi w,b,ξ 的极小,再对其求 α \alpha α 的极大。首先求 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ) 关于 w , b , ξ w, b, \xi w,b,ξ 的偏导,如下:
∂ L ∂ w = w − ∑ i = 1 N α i y i x i = 0 (9-42) \frac{\partial L}{\partial w} = w - \sum_{i=1}^{N} \alpha_i y_i x_i = 0 \tag{9-42} ∂w∂L=w−i=1∑Nαiyixi=0(9-42)
∂ L ∂ b = − ∑ i = 1 N α i y i = 0 (9-43) \frac{\partial L}{\partial b} = - \sum_{i=1}^{N} \alpha_i y_i = 0 \tag{9-43} ∂b∂L=−i=1∑Nαiyi=0(9-43)
∂ L ∂ ξ i = C − α i − μ i = 0 (9-44) \frac{\partial L}{\partial \xi_i} = C - \alpha_i - \mu_i = 0 \tag{9-44} ∂ξi∂L=C−αi−μi=0(9-44)
可解得:
w = ∑ i = 1 N α i y i x i (9-45) w = \sum_{i=1}^{N} \alpha_i y_i x_i \tag{9-45} w=i=1∑Nαiyixi(9-45)
∑ i = 1 N α i y i = 0 (9-46) \sum_{i=1}^{N} \alpha_i y_i = 0 \tag{9-46} i=1∑Nαiyi=0(9-46)
C − α i − μ i = 0 (9-47) C - \alpha_i - \mu_i = 0 \tag{9-47} C−αi−μi=0(9-47)
将式(9-45)~式(9-47)代入式(9-41),有:
min w , b , ξ L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i (9-48) \min_{w,b,\xi} \quad L(w, b, \xi, \alpha, \mu) = - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^{N} \alpha_i \tag{9-48} w,b,ξminL(w,b,ξ,α,μ)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi(9-48)
然后对 min w , b , ξ \min_{w,b,\xi} minw,b,ξ L ( w , b , ξ , α , μ ) L(w,b,\xi,\alpha,\mu) L(w,b,ξ,α,μ) 求 α \alpha α 的极大,可得对偶问题为:
max α L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i s . t . ∑ i = 1 N α i y i = 0 C − α i − μ i = 0 α i ≥ 0 μ i ≥ 0 , i = 1 , 2 , … , N (9-49) \begin{aligned} & \max_\alpha L(w,b,\xi,\alpha,\mu) = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^N \alpha_i \\ & s.t. \quad \sum_{i=1}^N \alpha_i y_i = 0 \\ & \quad C - \alpha_i - \mu_i = 0 \\ & \quad \alpha_i \geq 0 \\ & \quad \mu_i \geq 0, \quad i = 1, 2, \dots, N \tag{9-49} \end{aligned} αmaxL(w,b,ξ,α,μ)=−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαis.t.i=1∑Nαiyi=0C−αi−μi=0αi≥0μi≥0,i=1,2,…,N(9-49)
将式(9-49)的第2~4个约束条件式进行变换,消除变量 μ i \mu_i μi 后可简化约束条件为:
0 ≤ α i ≤ C (9-50) 0 \leq \alpha_i \leq C \tag{9-50} 0≤αi≤C(9-50)
联合式(9-48)和式(9-49),并将极大化问题转化为极小化问题,即式(9-40)的对偶问题。跟线性可分支持向量机求解方法一样,近似线性可分问题也是通过求解对偶问题而得到原始问题的解,进而确定线性分隔超平面和分类决策函数。
假设 α ∗ = ( α 1 ∗ , α 2 ∗ , … , α N ∗ ) T \alpha^* = (\alpha_1^*, \alpha_2^*, \dots, \alpha_N^*)^T α∗=(α1∗,α2∗,…,αN∗)T 是对偶最优化问题式(9-40)的解,根据拉格朗日对偶理论相关推论,式(9-40)满足KKT(Karush-Kuhn-Tucker)条件,有:
∂ L ∂ w = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 (9-51) \frac{\partial L}{\partial w} = w^* - \sum_{i=1}^N \alpha_i^* y_i x_i = 0 \tag{9-51} ∂w∂L=w∗−i=1∑Nαi∗yixi=0(9-51)
∂ L ∂ b = − ∑ i = 1 N α i ∗ y i = 0 (9-52) \frac{\partial L}{\partial b} = -\sum_{i=1}^N \alpha_i^* y_i = 0 \tag{9-52} ∂b∂L=−i=1∑Nαi∗yi=0(9-52)
∂ L ∂ ξ = C − α ∗ − μ ∗ = 0 (9-53) \frac{\partial L}{\partial \xi} = C - \alpha^* - \mu^* = 0 \tag{9-53} ∂ξ∂L=C−α∗−μ∗=0(9-53)
α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0 (9-54) \alpha_i^*(y_i(w^* \cdot x_i + b^*) - 1 + \xi_i^*) = 0 \tag{9-54} αi∗(yi(w∗⋅xi+b∗)−1+ξi∗)=0(9-54)
μ i ∗ ξ i ∗ = 0 (9-55) \mu_i^* \xi_i^* = 0 \tag{9-55} μi∗ξi∗=0(9-55)
y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ≥ 0 (9-56) y_i(w^* \cdot x_i + b^*) - 1 + \xi_i^* \geq 0 \tag{9-56} yi(w∗⋅xi+b∗)−1+ξi∗≥0(9-56)
ξ i ∗ ≥ 0 (9-57) \xi_i^* \geq 0 \tag{9-57} ξi∗≥0(9-57)
α i ∗ ≥ 0 (9-58) \alpha_i^* \geq 0 \tag{9-58} αi∗≥0(9-58)
μ i ∗ ≥ 0 , i = 1 , 2 , … , N (9-59) \mu_i^* \geq 0, \quad i = 1, 2, \dots, N \tag{9-59} μi∗≥0,i=1,2,…,N(9-59)
可解得:
w ∗ = ∑ i = 1 N α i ∗ y i x i (9-60) w^* = \sum_{i=1}^N \alpha_i^* y_i x_i \tag{9-60} w∗=i=1∑Nαi∗yixi(9-60)
b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) (9-61) b^* = y_j - \sum_{i=1}^N \alpha_i^* y_i (x_i \cdot x_j) \tag{9-61} b∗=yj−i=1∑Nαi∗yi(xi⋅xj)(9-61)
以上就是近似线性可分支持向量机的基本推导过程。从过程来看,近似线性可分问题求解推导与线性可分问题的求解推导非常类似。
以下是部分公式更加详细的解释:
公式 9-37
公式 9-38
公式 9-40
公式 9-41
公式 9-50
公式 9-51 ~ 9-59
相关文章:

近似线性可分支持向量机的原理推导
近似线性可分的意思是训练集中大部分实例点是线性可分的,只是一些特殊实例点的存在使得这种数据集不适用于直接使用线性可分支持向量机进行处理,但也没有到完全线性不可分的程度。所以近似线性可分支持向量机问题的关键就在于这些少数的特殊点。 相较于…...

Golang开发环境
Golang开发环境搭建 Go 语言开发包 国外:https://golang.org/dl/ 国内(推荐): https://golang.google.cn/dl/ 编辑器 Golang:https://www.jetbrains.com/go/ Visual Studio Code: https://code.visualstudio.com/ 搭建 Go 语言开发环境,需要…...

测试华为GaussDB(DWS)数仓,并通过APISQL快速将(表、视图、存储过程)发布为API
华为数据仓库服务 数据仓库服务(Data Warehouse Service,简称DWS)是一种基于公有云基础架构和平台的在线数据处理数据库,提供即开即用、可扩展且完全托管的分析型数据库服务。DWS是基于华为融合数据仓库GaussDB产品的云原生服务&a…...

使用GetX实现GetPage中间件
前言 GetX 中间件(Middleware)是 GetX 框架中的一种机制,用于在页面导航时对用户进行权限控制、数据预加载、页面访问条件设置等。通过使用中间件,可以有效地控制用户的访问流程,并在适当条件下引导用户到所需页面。 这…...

Navicat 17 功能简介 | SQL 预览
Navicat 17 功能简介 | SQL 预览 随着 17 版本的发布,Navicat 也带来了众多的新特性,包括兼容更多数据库、全新的模型设计、可视化智能 BI、智能数据分析、可视化查询解释、高质量数据字典、增强用户体验、扩展MongoDB 功能、轻松固定查询结果、便捷URI …...

ubuntu、Debian离线部署gitlab
一、软件包下载 gitlab安装包下载链接 ubuntu: ubuntu/focal 适用于 ubuntu20系列 ubuntu/bionic 适用于 ubuntu18 系列 Debian: debian/buster 适用于 Debian10系列 debian/bullseye 适用于 Debian11、12系列 二、安装gitlab ubuntu需要安装一些环境…...

数据库编程 SQLITE3 Linux环境
永久存储程序数据有两种方式: 用文件存储用数据库存储 对于多条记录的存储而言,采用文件时,插入、删除、查找的效率都会很差,为了提高这些操作的效率,有计算机科学家设计出了数据库存储方式 一、数据库 数据库的基本…...

独孤思维:总有一双眼睛默默观察你做副业
01 独孤昨天在陪伴群,分享了近期小白做副业的一些困扰。 并且以自己经历作为案例,分享了一些经验和方法。 最后顺势推出xx博主的关于365条赚钱信息小报童专栏。 订阅后,可以开拓副业赚钱思路,避免走一些弯路。 甚至于&#x…...

医院信息化与智能化系统(10)
医院信息化与智能化系统(10) 这里只描述对应过程,和可能遇到的问题及解决办法以及对应的参考链接,并不会直接每一步详细配置 如果你想通过文字描述或代码画流程图,可以试试PlantUML,告诉GPT你的文件结构,让他给你对应…...

基于YOLO11/v10/v8/v5深度学习的危险驾驶行为检测识别系统设计与实现【python源码+Pyqt5界面+数据集+训练代码】
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...

Flink CDC系列之:学习理解核心概念——Transform
Flink CDC系列之:学习理解核心概念——Transform Transform参数元数据字段函数比较函数逻辑函数字符串函数时间函数条件函数 示例添加计算列参考元数据列使用通配符投影所有字段添加过滤规则重新分配主键重新分配分区键指定表创建配置分类映射用户定义函数已知限制 …...
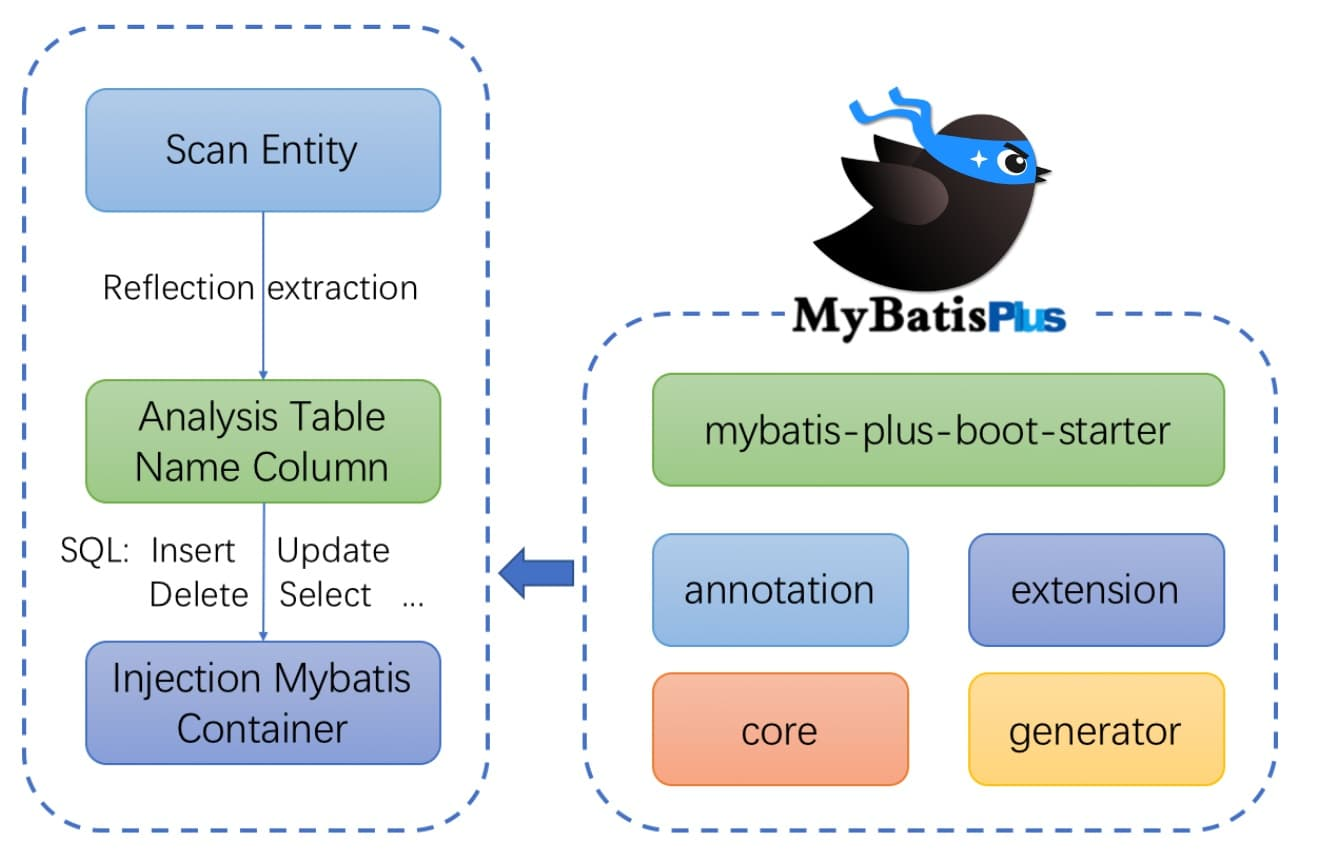
MyBatis-Plus:简化 CRUD 操作的艺术
一、关于MyBatis-Plus 1.1 简介 MyBatis-Plus 是一个基于 MyBatis 的增强工具,它旨在简化 MyBatis 的使用,提高开发效率。 关于Mybatis 简介 MyBatis 是一款流行的 Java 持久层框架,旨在简化 Java 应用程序与数…...

Windows on ARM编译安装openBLAS
Windows on ARM编译安装openBLAS 要求下载源码OpenBLAS可以使用LLVM工具链(clang-cl和flang)从源代码为Windows on ARM(WoA)进行构建。v0.3.24版本(预构建包)的构建和测试已通过。 要求 LLVM:版本需大于等于17.0.4 LLVM版本16及以下会生成冲突的符号(如_QQ*等)。 LL…...

FPGA编程语言VHDL与Verilog的比较分析!!!
VHDL(VHSIC硬件描述语言)和Verilog都是用于硬件描述和FPGA编程的工业标准语言。它们在语法和设计理念上存在一些差异,以下是两者的比较分析: 1. 历史背景 VHDL: 开发于1980年代初期,最初用于美国国防部的…...
)
C语言——八股文(笔试面试题)
1、 什么是数组指针,什么是指针数组? 数组指针:指向数组的指针 指针数组:数组中的元素都是指针 2、 什么是位段,什么是联合体 位段(Bit Field):在C语言中,允许在一个整数…...

解决 Oracle 数据库错误 ORA-12516:监听器无法找到匹配协议栈的处理程序
在使用 Oracle 数据库时,有时会遇到错误 ORA-12516,这个错误表明 Oracle 数据库的监听器无法为新的连接请求找到一个可用的处理程序,这通常是因为达到了连接数上限、配置问题或资源限制。本文将详细介绍如何解决这个问题。 一、错误描述 当…...

Flarum:简洁而强大的开源论坛软件
Flarum简介 Flarum是一款开源论坛软件,以其简洁、快速和易用性而闻名。它继承了esoTalk和FluxBB的优良传统,旨在提供一个不复杂、不臃肿的论坛体验。Flarum的核心优势在于: 快速、简单: Flarum使用PHP构建,易于部署&…...

方法+数组
1. 方法 1. 什么是方法 方法定义: // []表示可写可不写[public] [static] type name ( [type formal , type formal , ...]){方法体;[return value ;] }[修饰符] 返回值类型 方法名称([参数类型 形参 , 参数类型 形参 ...]){方法体代码;[return 返回值…...

驱动-----adc
在key1.c的基础上进行对adc1.c进行编写 首先将文件里面的key全部改为adc 再修改一下设备号 按键和adc的区别是什么,按键只需要按一下就触发了,并且不需要返回一个值出来, adc要初始化,启动,返回值 以下是裸机adc的代码: #include <s3c2440.h> #include "ad…...

js实现点击图片,使图片跟随鼠标移动(把注释打开是图片随机位置)
代码: <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Document</title>&l…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
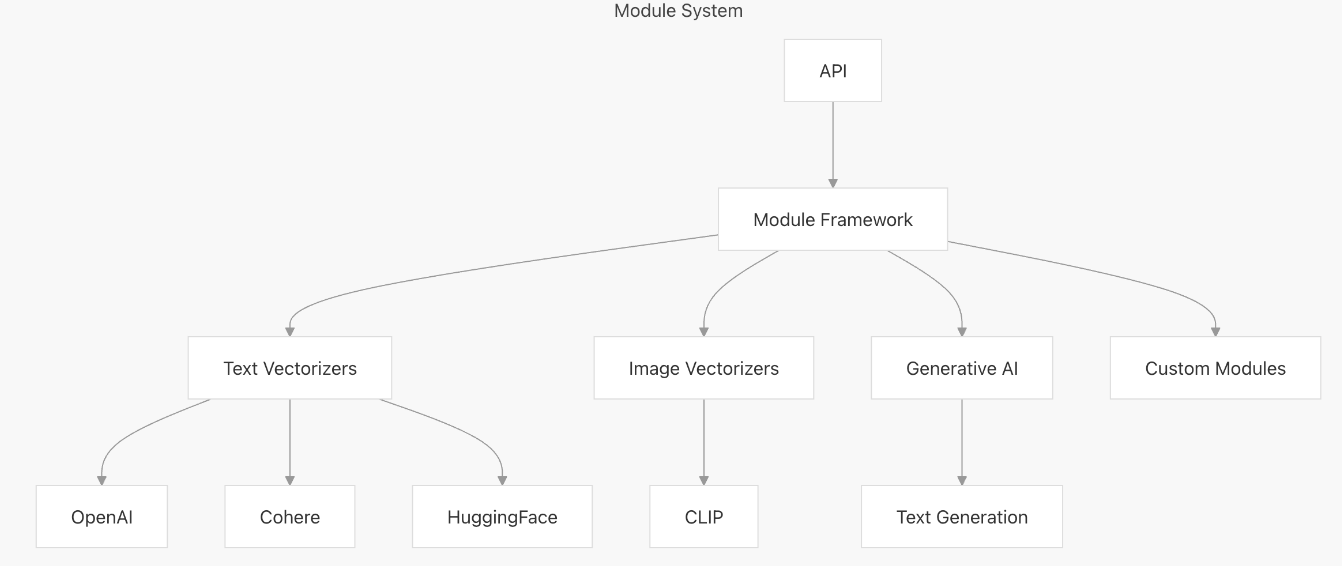
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...

2025-06-01-Hive 技术及应用介绍
Hive 技术及应用介绍 参考资料 Hive 技术原理Hive 架构及应用介绍Hive - 小海哥哥 de - 博客园https://cwiki.apache.org/confluence/display/Hive/Home(官方文档) Apache Hive 是基于 Hadoop 构建的数据仓库工具,它为海量结构化数据提供类 SQL 的查询能力…...
