机器学习算法之回归算法
一、回归算法思维导图

二、算法概念、原理、应用场景和实例代码
1、线性回归
1.1、概念
线性回归算法是一种统计分析方法,用于确定两种或两种以上变量之间的定量关系。 线性回归算法通过建立线性方程来预测因变量(y)和一个或多个自变量(x)之间的关系。其基本形式为 y = wx + e,其中 w 是权重,x 是自变量,e 是误差项。
1.2、算法原理
线性回归算法的核心在于找到最佳的拟合直线,使得预测值与实际值之间的误差最小。这通常通过最小二乘法来实现,即最小化预测值与实际值之差的平方和。线性回归可以分为一元线性回归和多元线性回归:
(1)一元线性回归:只有一个自变量 x 和一个因变量 y。 (2)多元线性回归:有多个自变量 x1, x2, …, xn 和一个因变量 y。
1.3、应用场景
线性回归算法广泛应用于各个领域,包括但不限于: (1)经济学:预测股票价格、经济增长等。
(2)医学:预测疾病发病率、药物效果等。
(3)环境科学:预测气候变化、污染水平等。
(4)市场营销:预测销售量、市场份额等。
1.4、公式推导
线性回归方程的推导过程包括以下几个步骤:
(1)计算平均值:分别计算 x 和 y 的平均值。
(2)计算分子和分母:使用最小二乘法计算回归系数 b 和 a。
(3)建立方程:最终得到线性回归方程 y = bx + a,其中 b 是斜率,a 是截距。
1.5、实例分析
假设有一组数据点 (x1, y1), (x2, y2), …, (xn, yn),线性回归的目标是找到一条直线 y = bx + a,使得所有数据点到这条直线的垂直距离的平方和最小。通过最小二乘法,可以求解出最佳的 b 和 a 值,从而得到具体的线性回归方程。
1.6、具体代码
鸢尾花数据集介绍
该数据集包含了三个品种的鸢尾花(Setosa、Versicolor、Virginica)每个品种各有50个样本,共计150个样本。对于每个样本,测量了4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度),以及其所属的品种标签。
数据集包括4个属性,分别为花萼的长、花萼的宽、花瓣的长和花瓣的宽。对花瓣我们可能比较熟悉,花萼是什么呢?花萼是花冠外面的绿色被叶,在花尚未开放时,保护着花蕾。四个属性的单位都是cm,属于数值变量,四个属性均不存在缺失值的情况,字段如下表所示:

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import matplotlib# 设置字体为SimHei,确保该字体在你的系统中存在
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号'-'显示为方块的问题# 加载鸢尾花数据集
def LoadIrisDataset():# 1.加载鸢尾花数据集iris = datasets.load_iris()X = iris.data # 特征数据,包含所有样本的4个特征y = iris.target # 目标变量,目前我们只使用第一个目标(0-1-2类)# 2.我们选择使用一个特征来进行线性回归,例如花瓣长度X = X[:, [2]] # 选择第三个特征:花瓣长度# 3.将数据集分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 4.创建线性回归模型model = LinearRegression()# 5.训练模型model.fit(X_train, y_train)# 6.预测测试集的结果y_pred = model.predict(X_test)# 7.评估模型性能mse = mean_squared_error(y_test, y_pred)r2 = r2_score(y_test, y_pred)# 8.模型评估print(f"系数(斜率): {model.coef_[0]}")print(f"截距: {model.intercept_}")print(f"均方误差 (MSE): {mse}")print(f"决定系数 (R²): {r2}")return X_test, y_test, y_pred# 二、绘制回归结果
def PlotResults(X_test, y_test, y_pred):plt.scatter(X_test, y_test, color="black", label="Data")plt.plot(X_test, y_pred, color="blue", linewidth=3, label="Linear Regression")plt.xlabel("花瓣长度 (cm)")plt.ylabel("目标值")plt.title("线性回归模型预测鸢尾花数据集")plt.legend()plt.show()if __name__ == "__main__":X_test, y_test, y_pred = LoadIrisDataset()PlotResults(X_test, y_test, y_pred)
控制台输出结果为:


2、岭回归
2.1、概念
岭回归(英文名:ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
2.2、算法原理

2.3、应用场景
(1)经济学:用于经济数据建模,以预测经济变量之间的关系。
(2)生物统计学:用于基因表达分析和生物信息学领域,以处理高维数据。
(3)工程学:用于工程建模和控制系统设计,以改善模型的鲁棒性。
(4)金融学:用于资产定价和风险管理,以降低投资组合的风险。
2.4、实例分析
这段代码实现了以下功能:
(1). 创建了一个具有10个特征的示例数据集,其中包含100个样本。
(2).将数据集划分为训练集和测试集,其中80%的数据用于训练,20%用于测试。
(3).使用scikit-learn库中的Ridge类定义了岭回归模型,并指定了岭参数(alpha)为1.0。
(4).在训练集上训练了岭回归模型。
(5).在测试集上进行了预测,并计算了预测结果与真实值之间的均方误差(MSE)。
(6).最后,绘制了预测值与真实值的对比图,以直观地展示模型的性能。
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_errordef TrainRidgeModel():# 1.创建示例数据集np.random.seed(0)X = np.random.rand(100, 10) # 100个样本,10个特征y = 2 * X[:, 0] + 3 * X[:, 1] + np.random.randn(100) # 构造线性关系,并添加噪声# 2.将数据集划分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 3.定义岭回归模型ridge = Ridge(alpha=1.0) # alpha为岭参数,默认为1.0# 4.在训练集上训练模型ridge.fit(X_train, y_train)# 5.在测试集上进行预测y_pred = ridge.predict(X_test)# 6.计算均方误差(MSE)作为性能评估指标mse = mean_squared_error(y_test, y_pred)print("岭回归模型的均方误差为:", mse)return y_test, y_preddef PlotPredictions(y_test, y_pred):# 1.绘制预测值与真实值的对比图plt.figure(figsize=(8, 6))plt.scatter(y_test, y_pred, color='blue')plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], linestyle='--', color='red')plt.xlabel('True Values')plt.ylabel('Predictions')plt.title('True vs. Predicted Values (Ridge Regression)')plt.show()if __name__ == '__main__':y_test, y_pred = TrainRidgeModel()PlotPredictions(y_test, y_pred)
控制台输出结果为:


3、Lasso回归
3.1、概念
岭回归是一种正则化技术,用于处理多重共线性问题。在标准线性回归中,模型试图找到最小化残差平方和的参数。然而,在存在高度相关特征的情况下,最小二乘估计可能会变得不稳定。为了克服这个问题,岭回归通过向损失函数添加一个惩罚项(即L2正则化项),使得模型系数变得更小,从而降低了过拟合的风险。
岭回归的目标函数是:
其中,λ 是正则化参数,控制着惩罚的强度。
特点:
(1).正则化类型: 使用L2正则化,也称为权重衰减。
(2).系数收缩: 岭回归通过添加平方项来收缩系数,但不会将它们缩减至零。
(3).多共线性处理: 对于具有多重共线性的数据集非常有效,因为它可以稳定系数估计。
(4).参数调整:正则化参数(λ)的选取对于模型性能至关重要。
3.2、应用场景
当数据集中存在高度相关的特征时。
当特征数量较大,但样本数量相对较少时。
当我们关心模型的解释性,而不是特征选择时。
3.3、实例分析
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import matplotlib# 设置字体为SimHei,确保该字体在你的系统中存在
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号'-'显示为方块的问题def LoadIrisAndPredict():# 1.加载鸢尾花数据集iris = datasets.load_iris()X = iris.data # 特征数据,包含所有样本的4个特征y = iris.target # 目标变量,目前我们只使用第一个目标(0-1-2类)# 2.我们选择使用一个特征来进行Lasso回归,例如花瓣长度X = X[:, [2]] # 选择第三个特征:花瓣长度# 3.将数据集分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 4.创建Lasso回归模型lasso_model = Lasso(alpha=1.0) # alpha是正则化强度# 5.训练模型lasso_model.fit(X_train, y_train)# 6.预测测试集的结果y_pred = lasso_model.predict(X_test)# 7.评估模型性能mse = mean_squared_error(y_test, y_pred)r2 = r2_score(y_test, y_pred)print(f"系数(斜率): {lasso_model.coef_[0]}")print(f"截距: {lasso_model.intercept_}")print(f"均方误差 (MSE): {mse}")print(f"决定系数 (R²): {r2}")return X_test, y_test, y_pred# 可视化结果
def VisualizeResults(X_test, y_test, y_pred):plt.scatter(X_test, y_test, color="black", label="Data")plt.plot(X_test, y_pred, color="blue", linewidth=3, label="Lasso Regression")plt.xlabel("花瓣长度 (cm)")plt.ylabel("目标值")plt.title("Lasso回归模型预测鸢尾花数据集")plt.legend()plt.show()if __name__ == "__main__":X_test, y_test, y_pred = LoadIrisAndPredict()VisualizeResults(X_test, y_test, y_pred)
运行结果为:


4、弹性网回归
4.1、概念
弹性网络回归(Elastic Net Regression)是岭回归(Ridge Regression)和Lasso回归(Lasso Regression)的结合。它通过引入两个正则化参数来实现特征选择和模型稳定性。弹性网络回归的损失函数结合了L1正则化和L2正则化,解决了Lasso在处理高相关特征时的缺陷,并且在处理高维数据时表现优异。
4.2、算法原理

4.3、应用场景和优势
弹性网络回归在处理多重共线性和特征选择方面特别有用。它结合了岭回归和Lasso回归的优点,适用于高维数据集,能够自动选择最重要的特征,同时保持模型的稳定性。弹性网络回归在生物信息学、金融数据分析等领域有广泛应用。
4.4、实例分析
在这里插入代码片


5、ARIMA
5.1、概念
ARIMA(AutoRegressive Integrated Moving Average)是一种用于时间序列预测的统计方法。它结合了自回归(Autoregressive, AR)、差分(Integrated,I)和移动平均(Moving Average, MA)三个部分,以建模和预测时间序列数据。
5.2、算法原理
(1)检查平稳性:首先需要确保时间序列数据是平稳的。如果数据不是平稳的,则需要通过差分使其变得平稳。
(2)确定参数 p、d 和 q:
1)选择合适的自回归阶数 ( p )。
2)确定使数据平稳所需的差分阶数 ( d )。
3)选择合适的移动平均阶数 ( q )。
(3)模型拟合:使用确定的参数进行模型拟合,以最小化预测误差。
(4)模型验证和评估:通过残差分析、AIC/BIC准则等方法来评估模型的性能,并进行必要的调整。
5.3、应用场景
(1)金融市场 股票价格预测:利用历史股价数据预测未来的股价走势。 汇率变动预测:通过观察历史汇率数据来预测未来汇率的变化。
(2)宏观经济分析 通货膨胀率预测:根据过去的通胀数据,预测未来的通货膨胀趋势。
GDP增长率预测:利用历史的经济数据来预测国家或地区的经济增长情况。
(3) 供应链管理
库存预测:通过历史销售数据来预测未来的需求量,从而更好地进行库存管理和优化。 生产计划制定:根据历史生产和销售数据来调整未来的生产计划。
(4)气象和环境科学 温度变化预测:利用过去的气温数据来预测未来几天或几周的天气情况。
空气质量预测:通过分析历史空气质量数据,预测未来的空气污染程度。
(5)销售预测
产品销量预测:根据过去的产品销售数据来预测未来的销售额,从而更好地进行库存管理和营销策略制定。
5.4、算法实例
假设我们有一个时间序列数据集,并且经过检验发现该数据是不平稳的。我们可以先应用一阶差分使其变得平稳(即 ( d = 1 )),然后选择合适的( p ) 和 ( q ) 值。假设通过试错法确定了 ( (p, d, q) = (2, 1, 2) ),那么模型可以表示为 ARIMA(2, 1, 2)。
使用Python实现ARIMA 在Python中,你可以使用statsmodels库来实现ARIMA模型。以下是一个简单的示例:
import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt
import matplotlib# 设置字体为SimHei,确保该字体在你的系统中存在
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号'-'显示为方块的问题def LoadIrisData():# 1.假设我们有一个时间序列数据集data = pd.read_csv('time_series_data.csv', parse_dates=['date'], index_col='date')data.index.freq = 'D' # 设置频率为每天# 2.检查数据平稳性并进行差分diff_data = data.diff().dropna()# 3.确定参数 p, d, qmodel = ARIMA(data, order=(2, 1, 2))results = model.fit()print(results.summary())# 4.预测未来值forecast_steps = 10forecast = results.get_forecast(steps=forecast_steps)mean_forecast = forecast.predicted_meanconf_int = forecast.conf_int()return data, mean_forecast, conf_int# 绘制预测结果
def PlotForecast(data, mean_forecast, conf_int):plt.figure(figsize=(14, 7))plt.plot(data, label='Original Data')plt.plot(mean_forecast.index, mean_forecast.values, color='red', label='Forecast')plt.fill_between(conf_int.index, conf_int.iloc[:, 0], conf_int.iloc[:, 1], color='pink', alpha=0.3)plt.legend()plt.show()if __name__ == '__main__':data, mean_forecast, conf_int = LoadIrisData()PlotForecast(data, mean_forecast, conf_int)
运行结果如下:


相关文章:

机器学习算法之回归算法
一、回归算法思维导图 二、算法概念、原理、应用场景和实例代码 1、线性回归 1.1、概念 线性回归算法是一种统计分析方法,用于确定两种或两种以上变量之间的定量关系。 线性回归算法通过建立线性方程来预测因变量(y)和一个或多个自变量…...

cordova android 内嵌vue页面 启动页之后白屏问题处理
困扰很久的问题 一直都用splash 做延迟加载 但在 一些android机器上还是会有 这短暂的白屏其实就是vue页面尚未完全渲染的间隙 处理方案 在html中添加 <body><div id"splash-screen" style"position: fixed; top: 0; left: 0; width: 100%; height: 1…...
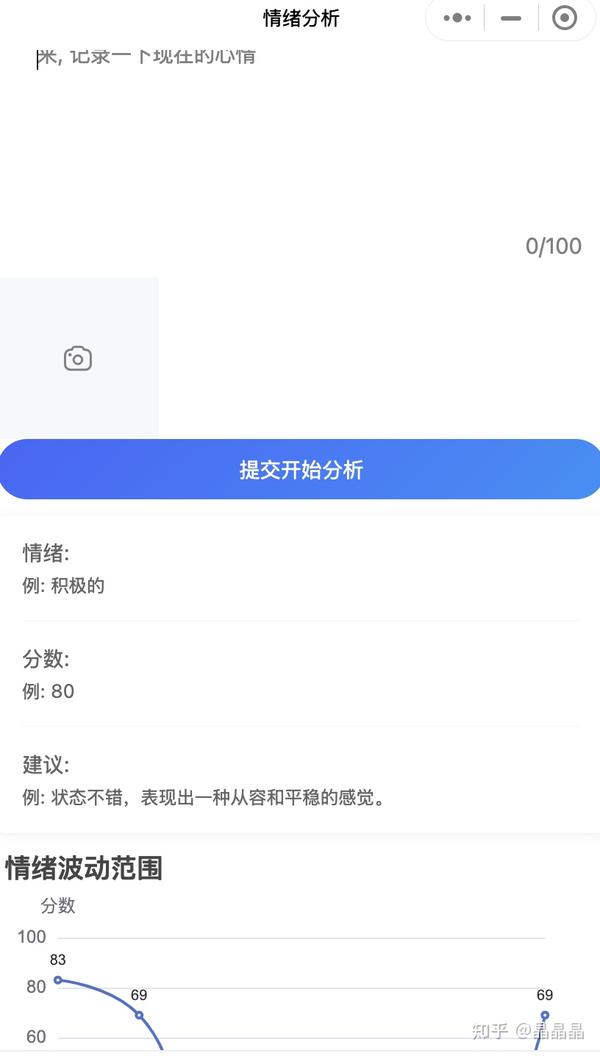
自研小程序-心情追忆
在近期从繁忙的工作中暂时抽身之后,我决定利用这段宝贵的时间来保持我的Java技能不致生疏,并通过一个个人项目来探索人工智能的魅力。 我在Hugging Face(国内镜像站点:HF-Mirror)上发现了一个关于情感分析的练习项目&…...

【部署与升级-会议签到的web安装】
部署与升级-会议的远程安装 技术路线界面规划flaskAPI以及socketio.emit shellout浏览器和后端交互到处是偶遇 技术路线 运行的基础是Flask-Soketio, 并借鉴了后台运行系统指令的代码 和scrncpy项目,app安装的脚本 #mermaid-svg-8H9rbzbpgpnAXfA3 {font-family:"trebuche…...

【jvm】如何设置新生代和老年代的比例
目录 1. 说明2. 使用-XX:NewRatio参数3. 使用-Xmn参数4. 配置新生区中的Eden区和Survivor区比例5. 综合配置示例6. 注意事项 1. 说明 1.新生代(Young Generation)和老年代(Old Generation)的比例可以通过特定的参数进行设置。2.这…...

系统学习CFD,常见收敛问题、及如何与机器学习相结合
一、如何系统学习CFD 系统学习计算流体力学(CFD)需要按照一定的步骤和层次进行,以下是一个学习路径的建议: 1.基础知识学习: 掌握流体力学的基本原理,包括流体静力学、流体动力学、流体控制方程等。 学习…...

REST架构与实现
一、REST 架构风格 基本概念 REST(Representational State Transfer),即表述性状态转移,是一种软件架构风格。它通过使用标准的 HTTP 方法操作网络上的资源来实现信息交互。在 REST 架构风格中,网络上的一切都被抽象成资源,例如,在一个在线购物系统中,商品、订单、用户…...
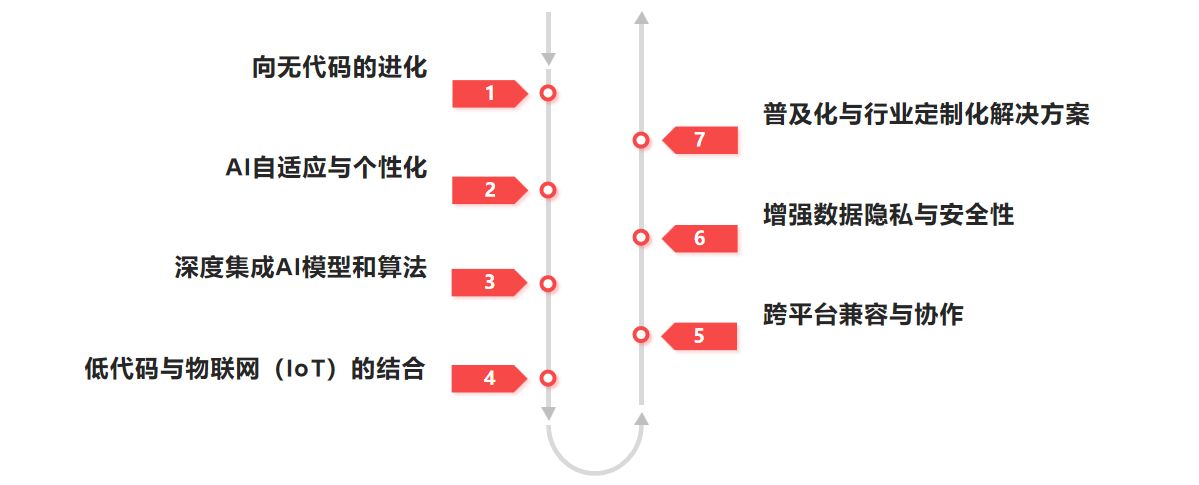
AI驱动的低代码未来:加速应用开发的智能解决方案
引言 随着数字化转型的浪潮席卷全球,企业对快速构建应用程序的需求愈发强烈。然而,传统的软件开发周期冗长、成本高昂,往往无法满足快速变化的市场需求。在此背景下,低代码平台逐渐成为开发者和企业的优选方案,以其“低…...

快速上手 Rust——环境配置与项目初始化
Rust 跨界:全面掌握跨平台应用开发 第一章:快速上手 Rust 1.1 环境配置与项目初始化 1.1.1 安装 Rust 和 Cargo 在开始学习 Rust 之前,首先需要安装 Rust 编程语言及其包管理工具 Cargo。Rust 的安装非常简单,使用官方的安装脚…...

分布式事务Seata-AT模式
1. seata安装 docker 安装 docker run --name seata-server \-p 8091:8091 \-p 7091:7091 \-e SEATA_IP192.168.0.250 \-e SEATA_PORT8091 \seataio/seata-server将安装好的配置文件数据,拷贝一份到物理机 docker cp seata-serve:/seata-server/resources /User/…...

编程知识概览
编程,这个在现代社会中无处不在的词汇,已经从最初的计算机专业人士的专属技能,变成了许多人日常生活和工作中不可或缺的一部分。从简单的网页浏览、邮件发送,到复杂的游戏开发、数据分析,编程的应用几乎覆盖了所有领域…...

基于 GADF+Swin-CNN-GAM 的高创新扰动信号识别模型!
往期精彩内容: Python-电能质量扰动信号数据介绍与分类-CSDN博客 Python电能质量扰动信号分类(一)基于LSTM模型的一维信号分类-CSDN博客 Python电能质量扰动信号分类(二)基于CNN模型的一维信号分类-CSDN博客 Python电能质量扰动信号分类(三)基于Transformer的一…...
 优化)
【Nextcloud】在 Ubuntu 22.04.3 LTS 上的 Nextcloud Hub 8 (29.0.0) 优化
[TOC](Nextcloud Hub 8 (29.0.0) 优化) Nextcloud 优化是个长期的过程,只能遇到问题解决问题了。遇到的问题和解决办法会逐步的编写完善。 打开 PHP 内存限制 伴随着内容增多,并添加更多的功能,访问 Nextcloud 变慢。通过修改PHP 内存限制&am…...

全渠道供应链打造中企业定制开发2+1链动模式S2B2C商城小程序的策略与影响
摘要:本文探讨了全渠道供应链打造对于零售企业的重要性及面临的挑战,着重分析了物流环节整合的难点,并以家电行业为例说明了节假日期间物流对企业经营的影响。同时,引入“企业定制开发21链动模式S2B2C商城小程序”这一关键因素&am…...

Github 2024-10-24 Go开源项目日报 Top10
根据Github Trendings的统计,今日(2024-10-24统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Go项目10Solidity项目1Ollama: 本地大型语言模型设置与运行 创建周期:248 天开发语言:Go协议类型:MIT LicenseStar数量:42421 个Fork数量:…...

中航资本:锂电行业现分化 优质产能仍然紧俏
2024年前三季度,受轻贱需求增速放缓影响,锂电工业堕入结构性供需错配,产品价格继续低迷,作业盈余全体承压。 当资料端不再稀缺,锂电作业由“卖方商场”转向“买方商场”,工业链博弈天平逐渐向轻贱倾斜。表…...
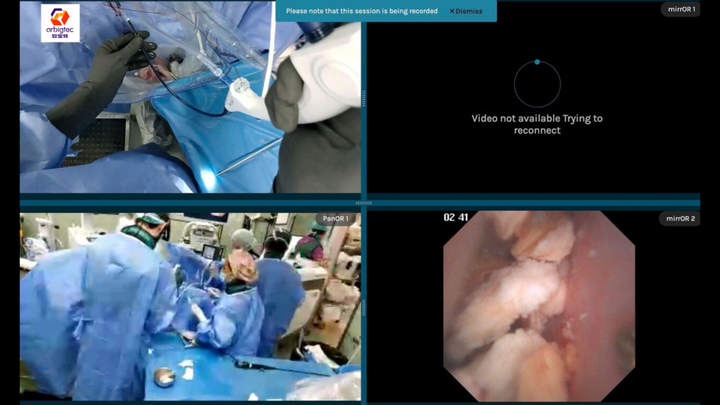
安宝特案例 | AR技术在院外心脏骤停急救中的革命性应用
00 案例背景 在院外心脏骤停 (OHCA) 的突发救援中,时间与效率直接决定着患者的生命。传统急救模式下,急救人员常通过视频或电话与医院医生进行沟通,以描述患者状况并依照指令行动。然而,这种信息传递方式往往因信息不完整或传递延…...

curl调用微信退款No required SSL certificate was sent
文章目录 前言一、错误一二、错误二 总结 前言 在之前的博客中提到微信证书到期了,需要更换,但是当我更换完证书自信满满的时候,却出现了两个问题,记录一下。 一、错误一 CURL Error: 58unable to load client key: -8178 (SEC_…...

进程守护SuperVisord内部的进程定时监测并重启
一个swoole的wensocket程序运行在SuperVisord下端口9503 设置一个每分钟任务监测9503的端口链接数,输出链接数,并在链接数为0的情况下重启wensocket进程。 以下截图是宝塔面板环境下 #!/bin/bash current$(date %H.%M) ws9503_procnumnetstat -nat | gre…...

[面试题]ES6 Javascript
ES6 箭头函数和普通函数有什么区别? 1)定义方式:箭头函数使用箭头(>)语法,省略了 function 关键字。 2)参数处理:如果只有一个参数,箭头函数可以省略括号。 3)函数体:如果函数体只有一条语句,箭头函数可以省略花括号和 return 关键字 4)…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

