当前位置： 首页 > news >正文

Kyber原理解析

news 2025/8/25 16:08:04

Kyber是一种IND-CCA2安全的密钥封装机制。Kyber的安全性基于在模格（MLWE问题）中解决LWE问题的难度。Kyber的构造采⽤两阶段⽅法：⾸先介绍⼀种⽤来加密固定32字节⻓度的消息原⽂的IND-CPA安全性的公钥加密⽅案，我们称之为 CPAPKE， CPAPKE由密钥生成（ CPAPKE.KeyGen）、加密（ CPAPKE.Encrypt）、解密（ CPAPKE.Decrypt）三个算法组成。然后，我们使⽤略微调整的Fujisaki-Okamoto（FO）变换来构建IND-CCA2安全性的CCAKEM，CCAKEM方案由密钥生成（CCAKEM.KeyGen）、封装（CCAKEM.Encaps）、解封装（CCAKEM.Decaps）三个算法组成。

由CPAPKE通过FO变换转换成CCAKEM并不复杂，本文我们主要举例解释一下CPAPKE的三个算法，Kyber出于安全性考虑，系统参数都较大，这里我们只为了简要解释原理，因此采用了压缩版的参数。假设q=17, 多项式模数f=x^4+1 。

1.密钥对生成

添加图片注释，不超过 140 字（可选）

对于密钥对生成阶段，我们会获得密钥对（pk,sk）,其中pk=t=As+e, sk=s。A，s, e都是随机生成的，我们假设其取值如图上所示，最终计算获得：t = (-15x^6-26x^5-41x^4-18x^3+8x, -11x^6-9x^5-23x^4-24x^3+x^2-15x)

由于多项式系数取值模数 f=x^4+1 ,可以简单理解为x^4=-1 ,对t进行转换：

t=(-15x^6-26x^5-41x^4-18x^3+8x,-11x^6-9x^5-23x^4-24x^3+x^2-15x)=(15x^2+26x+41-18x^3+8x,11x^2+9x+23-24x^3+x^2-15x)=(-18x^3+15x^2+34x+41,-24x^3+12x^2-6x+23)

（将x^4 转换为-1）

又由于q=17, 我们进一步对系数取模得到：

t=(16x^3+15x^2+7,10x^3+12x^2+11x+6)

综上，密钥生成阶段我们生成了密钥对pk=(16x^3+15x^2+7,10x^3+12x^2+11x+6),sk=(-x^3-x^2+x,-x^3-x)

2.密钥封装

添加图片注释，不超过 140 字（可选）

密钥封装阶段我们从公钥中恢复了种子 ρ ，从而恢复出密钥对生成阶段的矩阵A，又随机生成了 r,e_1,e_2 , 并假设我们的输入 message=(11)_{10}=(1011)_2 .转化为多项式系数后 m_b=x^3+x+1

添加图片注释，不超过 140 字（可选）

Decompressq(m_b,1)=q/2 \ast m_b=9m_b=9x^3+9x+9 ,

再结合之前生成的 ，A，r, e_1,e_2 , 计算 u=A^Tr+e_1=(11x^3+11x^2+10x+3,4x^3+4x^2+13x+11)

v=t^Tr+e_2+Decompress_q(m_b,1)=7x^3+6x^2+8x+15

3.密钥解封装

添加图片注释，不超过 140 字（可选）

根据密钥封装阶段的u,v和密钥对生成阶段的sk, 我们计算出密钥解封装阶段的 m_n=8x^3+14x^2+8x+6 ,最后我们将 m_n的多项式系数与 q/2 ， 0 对比并取round，获取了round后的多项式 m_{round}=9x^3+9x+9 ,最终我们计算 m_b=1/9\ast m_{round}=x^3+x+1=1x^3+0x^2+1x+1 ,取系数得 message=(1011)_2=(11)_{10}.

相关文章：

Kyber原理解析

Kyber是一种IND-CCA2安全的密钥封装机制。Kyber的安全性基于在模格（MLWE问题）中解决LWE问题的难度。Kyber的构造采⽤两阶段⽅法：⾸先介绍⼀种⽤来加密固定32字节⻓度的消息原⽂的IND-CPA安全性的公钥加密⽅案，我们称之为 CPAPKE&a…...

编程日记 2024/10/31 17:30:05

2024 CCF CSP-J/S 2024 第二轮认证 真题试卷

2024年信息学奥赛CSP-J2入门级复赛真题试卷 题目总数：4 总分数：400 编程题 第 1 题 问答题 扑克牌(poker) 【题目描述】 小 P 从同学小 Q 那儿借来一副 n 张牌的扑克牌。 本题中我们不考虑大小王，此时每张牌具有两个属性:花色和…...

编程日记 2024/10/31 17:28:02

Android 无障碍服务常见问题梳理

android 无障碍服务本意是为了帮助盲人操作手机而设计，但是现在也有人利用这个做自动化操作。 本片文章讲述的主要用作自动化方面。 官方文档 关于配置方法和接口列表，参考 无障碍 比较常用的接口： 1. 执行点击操作 2. 触摸屏幕&#xf…...

编程日记 2024/10/31 17:27:00

Milvus 与 Faiss：选择合适的向量数据库

向量数据库 Milvus 和 Faiss 都是处理大规模向量数据的工具，尤其适用于需要相似性搜索的场景，比如推荐系统、图像检索和自然语言处理等。但它们各自的设计初衷和功能有所不同，适用于不同的使用场景。下面，我们从性能、功能特性、部…...

编程日记 2024/10/31 17:23:56

2024最全CTF入门指南、CTF夺旗赛及刷题网站（建议收藏！）

文章目录 一、赛事介绍二、竞赛模式三、CTF各大题型简介四、赛题情况分析CTF 工具集合Web | Web 安全🕸 MISC | 杂项❆ 基础工具❆ 解题工具❆ 开源脚本🔑 Crypto | 密码学 💫 Reverse | 逆向基础工具💥 PWN | 二进制 &#x1f44…...

编程日记 2024/10/31 17:21:54

【论文阅读】ESRGAN+

学习资料 论文题目：进一步改进增强型超分辨率生成对抗网络（ESRGAN : FURTHER IMPROVING ENHANCED SUPER-RESOLUTION GENERATIVE ADVERSARIAL NETWORK）论文地址：2001.08073代码：ncarraz/ESRGANplus： ICASSP …...

编程日记 2024/10/31 17:16:46

北京市首发教育领域人工智能应用指南，力推个性化教育新篇章

近年来，人工智能在全球教育领域的应用呈现蓬勃发展之势，各国都在探索如何将其更好的融入教育体系，在这一背景下，北京市于10月26日发布《北京市教育领域人工智能应用指南》（以下简称《指南》），推…...

编程日记 2024/10/31 17:13:43

【Java并发编程】信号量Semaphore详解

一、简介 Semaphore（信号量）：是用来控制同时访问特定资源的线程数量，它通过协调各个线程，以保证合理的使用公共资源。 Semaphore 一般用于流量的控制，特别是公共资源有限的应用场景。例如数据库的连接&am…...

编程日记 2024/10/31 17:10:40

window11使用wsl2安装Ubuntu22.04

目录 1、快速了解wsl2 安装子系统linux流程（B站视频） 2、wsl2常用命令 3、windows与子系统Linux文件访问方法 4、子系统linux使用windows网络代理、网络配置（镜像网络，非NAT） 5、wsl2 Ubuntu miniconda 安装 6、…...

编程日记 2024/10/31 17:09:39

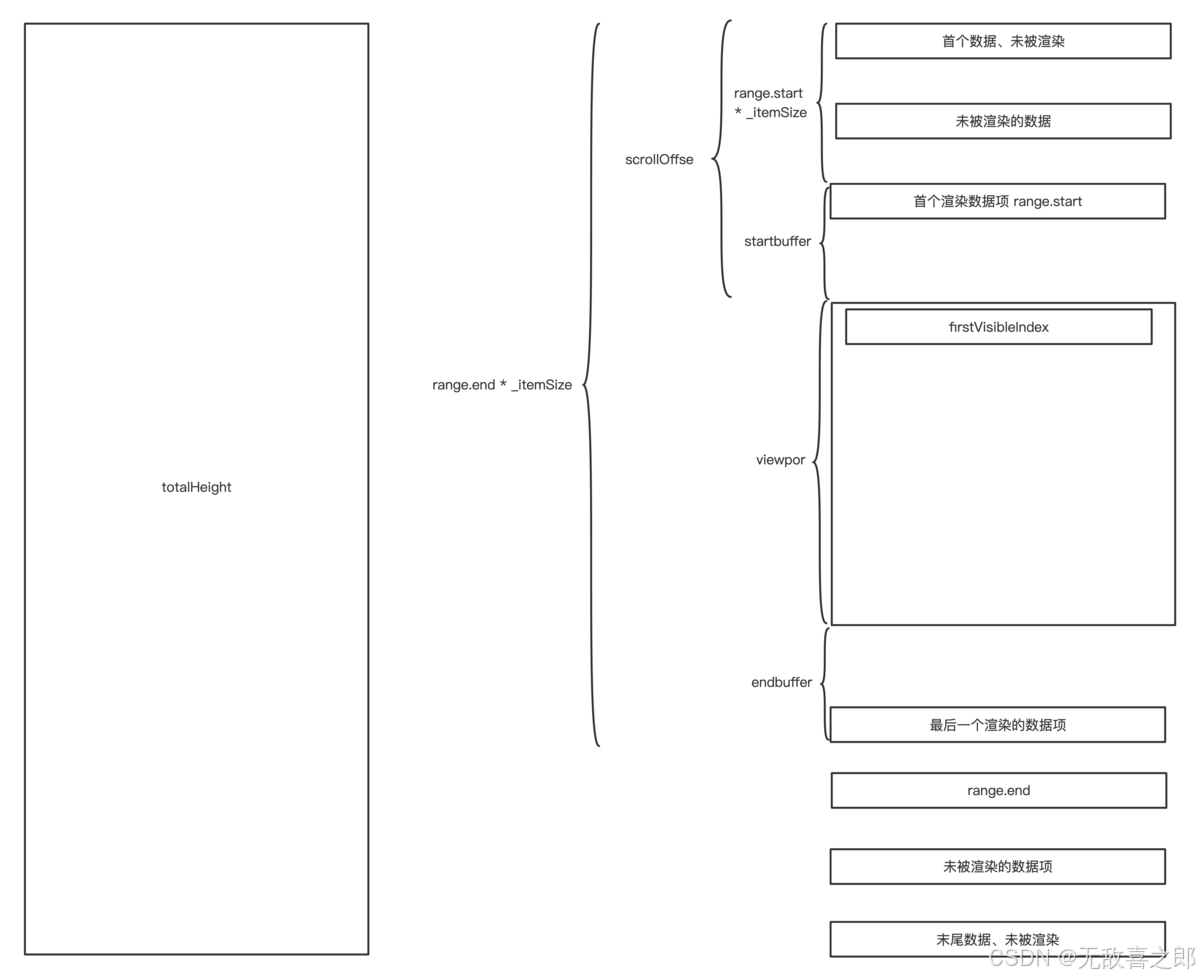
虚拟滚动 - 从基本实现到 Angular CDK

简介 在大数据列表的处理上，虚拟滚动是一种优化性能的有效方式。本篇文章将详细介绍两种常见的虚拟滚动实现方式：使用 transform 属性和 Intersection Observer。重点讲解如何通过 transform 属性实现高效的虚拟滚动，并对比Angular CDK中的实…...

编程日记 2024/10/31 17:08:37

Spring WebFlux学习笔记（一）

核心思想 WebFlux主要是异步 例子 参考一个源码&#xff1a; https://blog.csdn.net/qq_43923045/article/details/106309432?spm1001.2014.3001.5506 GetMapping("/delay1")public Mono<RestResult> delayResult() {long l System.currentTimeMillis();…...

编程日记 2024/10/31 17:03:32

富格林：正确追损思维安全交易

富格林指出&#xff0c;对于如何正确追损的这个问题是需要持续付出时间和精力的&#xff0c;发现具备耐心的投资者往往在正确追损的路上更加游刃有余。他们总是可以保持较为平和的心态&#xff0c;不急不躁地分析原因并通过自身掌握的安全应对措施来进行交易。富格林在以下分享…...

编程日记 2024/10/31 17:02:29

前端vue2迁移至uni-app

1.确定文件存放位置 components: 继续沿用 pages: views内容移动到pages static: assets内容移动到static uni_modules: uni-app的插件存放位置 迁移前 src├─assets│ └─less├─components│ ├─common│ │ ├─CommentPart│ │ └─MessDetail│ ├─home│…...

编程日记 2024/10/31 17:01:25

恋爱脑学Rust之闭包三Traits：Fn，FnOnce，FnMut

在Rust中&#xff0c;FnOnce、FnMut和Fn是三个用于表示闭包&#xff08;closure&#xff09;类型的trait。闭包是一种特殊的函数&#xff0c;它可以捕获其环境变量&#xff0c;即在其定义时所处的作用域中的变量。以下是关于这三个trait的详细介绍&#xff1a; 1. FnOnce&#…...

编程日记 2024/10/31 17:00:24

区块链介绍

区块链&#xff08;英文名&#xff1a;blockchain或block chain&#xff09;是一种块链式存储、不可篡改、安全可信的去中心化分布式账本&#xff0c;它结合了分布式存储、点对点传输、共识机制、密码学等技术&#xff0c;通过不断增长的数据块链&#xff08;Blocks&#xff09…...

编程日记 2024/10/31 16:58:22

git回滚间隔的提交

如果你需要回滚几个非连续的提交&#xff0c;可以使用 git revert 来选择性地撤销这些提交。这样做不会改变提交历史&#xff0c;只是会在当前分支上创建新的提交来反转指定的更改。 ### 使用 git revert 回滚间隔的提交 1. **查看提交历史**&#xff1a; 首先&#xff0c…...

编程日记 2024/10/31 16:56:20

Map和Set（数据结构）

一、概念 Map 和 set 是一种专门用来进行搜索的容器或者数据结构&#xff0c;其搜索的效率与其具体的实例化子类有关。 Map 和 Set 是一种适合动态查找的集合容器。 模型 一般把搜索的数据称为关键字&#xff08; Key &#xff09;&#xff0c;和关键字对应的称为值&#xff0…...

编程日记 2024/10/31 16:52:16

vue3uniapp实现自定义拱形底部导航栏，解决首次闪烁问题

前言&#xff1a; 我最初在网上翻阅查找了很多方法&#xff0c;发现大家都是说在page.json中tabbar中添加&#xff1a;"custom": true,即可解决首次闪烁的问题&#xff0c;可是添加了我这边还是会闪烁&#xff0c;因此我这边改变了思路&#xff0c;使用了虚拟页面来解…...

编程日记 2024/10/31 16:51:14

新需求编码如何注意低级错误代码

1. 日常开发常见错误问题 变量拷贝未修改变量定义的值刚开始是随意写的一个值&#xff0c;想等到上线的时候再改成正确的&#xff0c;但是上线的时候忘记改了程序常量配置的错误逻辑关系判断错误 常见的如都不为null、都不为空集合判断不为空逻辑取反了多个关系的 && …...

编程日记 2024/10/31 16:48:11

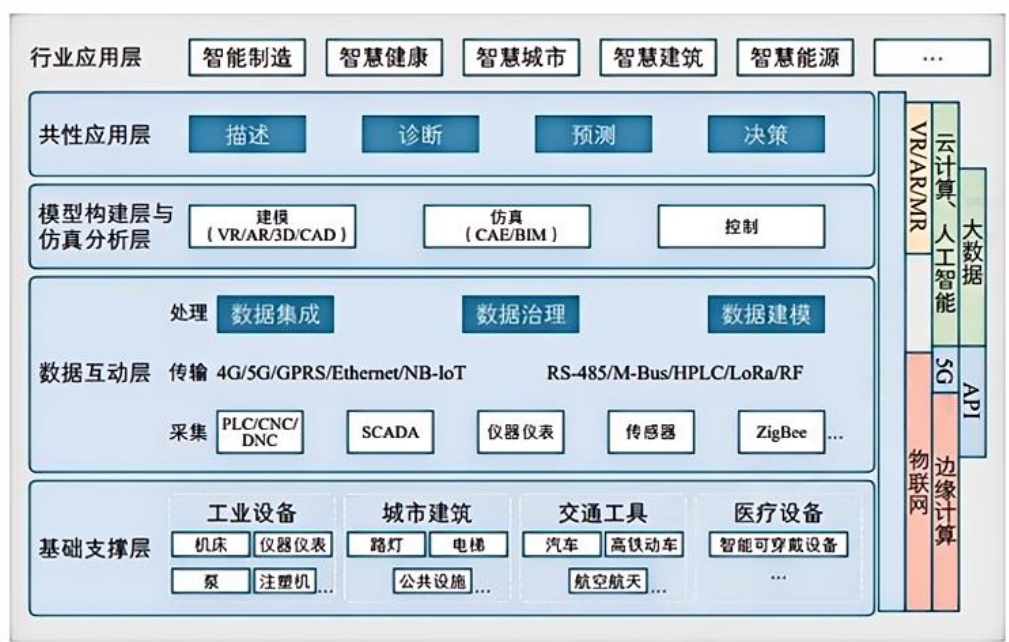
系统架构图设计（行业领域架构）

物联网 感知层&#xff1a;主要功能是感知和收集信息。感知层通过各种传感器、RFID标签等设备来识别物体、采集信息&#xff0c;并对这些信息进行初步处理。这一层的作用是实现对物理世界的感知和初步处理&#xff0c;为上层提供数据基础网络层&#xff1a;网络层负责处理和传输…...

编程日记 2024/10/31 16:47:10

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2025/8/7 7:40:03

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销&#xff0c;平衡网络负载&#xff0c;延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

编程新知 2025/8/22 2:47:24

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2025/8/25 10:12:48

LeetCode - 394. 字符串解码

题目 394. 字符串解码 - 力扣&#xff08;LeetCode&#xff09; 思路 使用两个栈&#xff1a;一个存储重复次数&#xff0c;一个存储字符串 遍历输入字符串&#xff1a; 数字处理&#xff1a;遇到数字时&#xff0c;累积计算重复次数左括号处理&#xff1a;保存当前状态&a…...

编程新知 2025/8/22 4:40:29

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2025/8/6 4:20:27

AI编程--插件对比分析：CodeRider、GitHub Copilot及其他

AI编程插件对比分析&#xff1a;CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展&#xff0c;AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者&#xff0c;分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

编程新知 2025/7/6 18:33:10

tree 树组件大数据卡顿问题优化

问题背景 项目中有用到树组件用来做文件目录&#xff0c;但是由于这个树组件的节点越来越多&#xff0c;导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多&#xff0c;导致的浏览器卡顿&#xff0c;这里很明显就需要用到虚拟列表的技术&…...

编程新知 2025/8/6 5:14:18

Swagger和OpenApi的前世今生

Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章&#xff0c;二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑&#xff1a; &#x1f504; 一、起源与初创期&#xff1a;Swagger的诞生&#xff08;2010-2014&#xff09; 核心…...

编程新知 2025/8/22 13:56:38

RabbitMQ入门4.1.0版本（基于java、SpringBoot操作）

RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发&#xff0c;后来由Pivotal Software Inc.&#xff08;现为VMware子公司&#xff09;接管。RabbitMQ 是一个开源的消息代理和队列服务器&#xff0c;用 Erlang 语言编写。广泛应用于各种分布…...

编程新知 2025/7/30 12:05:00

stm32wle5 lpuart DMA数据不接收

配置波特率9600时&#xff0c;需要使用外部低速晶振...

编程新知 2025/8/22 6:01:37