【二叉树】C非递归算法实现二叉树的先序、中序、后序遍历
引言:
遍历二叉树:指按某条搜索路径巡访二叉树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。
除了层次遍历外,二叉树有三个重要的遍历方法:先序遍历、中序遍历、后序遍历。
1、递归算法实现先序、中序、后序遍历:
(1)先序遍历:
void PreOrderTraverse(BiTree T)
{if(T){cout<<T->data;PreOrderTraverse(T->lchild);PreOrderTraverse(T->rchild);}
}
(2)中序遍历:
void InOrderTraverse(BiTree T)
{ if(T){InOrderTraverse(T->lchild);cout<<T->data;InOrderTraverse(T->rchild);}
} (3)后序遍历
void PostOrderTraverse(BiTree T)
{ if(T){ PostOrderTraverse(T->lchild); PostOrderTraverse(T->rchild); cout<<T->data; }
}
2.非递归算法实现先序、中序、后序遍历:
采用非递归算法则需要利用栈来实现对二叉树的遍历:
(1)先序遍历非递归算法
void PreOrder_non_recursion(BiTree T)//先序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p,q;p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); cout<<p->data; //访问根节点 p=p->lchild; //遍历左子树 }else{Pop(S,*q);p=q->rchild; //遍历右子树 }}
}
(2)中序遍历非递归算法
void InOrder_non_recursion(BiTree T)//中序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p; BiTree q; p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); p=p->lchild; //遍历左子树 }else{Pop(S,*q);cout<<q->data; //访问根节点 p=q->rchild; //遍历右子树 }}
}
(3)后序遍历非递归算法
(采用非递归算法实现对二叉树的后序遍历,会稍微复杂一些,本算法借用了两个栈结构)
void PostOrder_non_recursion(BiTree T)//后序遍历的非递归算法
{LinkStack l_S,r_S;InitStack (l_S);InitStack (r_S);BiTree p,q; p=T;Push(l_S,*p);while(!StackEmpty(l_S)){Pop(l_S, *q);Push(r_S,*q);if(q->lchild){Push(l_S, *q->lchild);}if(q->rchild){Push(l_S,*q->rchild);}}while(!StackEmpty(r_S)){Pop(r_S,*q);cout<<q->data;}
}
3.完整代码
1、采用按照先序遍历的顺序建立二叉链表,用‘#’表示空树。如图所示:

2、先序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void PreOrder(BiTree T){ //先序遍历的递归递归算法if(T){cout<<T->data;PreOrder(T->lchild);PreOrder(T->rchild);}
}void PreOrder_non_recursion(BiTree T)//先序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p,q;p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); cout<<p->data; //访问根节点 p=p->lchild; //遍历左子树 }else{Pop(S,*q);p=q->rchild; //遍历右子树 }}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"先序序列(递归算法):"; PreOrder(T); cout<<"\n先序序列(非递归算法):"; PreOrder_non_recursion(T);return 0;
}实验结果:

3、中序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void InOrder(BiTree T){ //中序遍历的递归递归算法if(T){InOrder(T->lchild);cout<<T->data;InOrder(T->rchild);}
}void InOrder_non_recursion(BiTree T)//中序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p; BiTree q; p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); p=p->lchild; //遍历左子树 }else{Pop(S,*q);cout<<q->data; //访问根节点 p=q->rchild; //遍历右子树 }}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"中序序列(递归算法):"; InOrder(T); cout<<"\n中序序列(非递归算法):"; InOrder_non_recursion(T);return 0;
}实验结果:

4、后序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void PostOrder(BiTree T){ //后序遍历的递归递归算法if(T){PostOrder(T->lchild);PostOrder(T->rchild);cout<<T->data;}
}void PostOrder_non_recursion(BiTree T)//后序遍历的非递归算法
{LinkStack l_S,r_S;InitStack (l_S);InitStack (r_S);BiTree p,q; p=T;Push(l_S,*p);while(!StackEmpty(l_S)){Pop(l_S, *q);Push(r_S,*q);if(q->lchild){Push(l_S, *q->lchild);}if(q->rchild){Push(l_S,*q->rchild);}}while(!StackEmpty(r_S)){Pop(r_S,*q);cout<<q->data;}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"中序序列(递归算法):"; PostOrder(T); cout<<"\n中序序列(非递归算法):"; PostOrder_non_recursion(T);return 0;
}实验结果:

欢迎大家一起来交流~
相关文章:

【二叉树】C非递归算法实现二叉树的先序、中序、后序遍历
引言: 遍历二叉树:指按某条搜索路径巡访二叉树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。 除了层次遍历外,二叉树有三个重要的遍历方法:先序遍历、中序遍历、后序遍历。 1、递归算法实现先序、中序、后…...

Android——事件冲突处理
当我们给列表的item设置了点击事件后,又给item中的按钮设置了点击事件,此时item的点击事件会失效。 解决 给item的布局xml中设置以下属性 android:descendantFocusability"blocksDescendants"<LinearLayout xmlns:android"http://sc…...

vue + elementui 全局Loading效果
注:在request请求和响应封装的文件里引入loading,发请求时打开loading,响应时关闭loading,这样每个接口调用时都会有loading效果 (1) 首先确保项目中安装了element-ui这个依赖包 npm i element-ui -S&…...
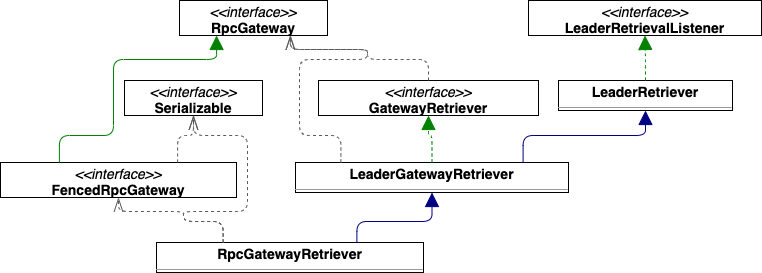
深度了解flink(十) JobManager(4) ResourceManager HA
ResourceManager(ZK模式)的高可用启动流程 ResourceManager启动流程在DefaultDispatcherResourceManagerComponentFactory#create中 public DispatcherResourceManagerComponent create(Configuration configuration,ResourceID resourceId,Executor i…...

【万兴科技-注册_登录安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

Android启动流程_Zygote阶段
前言 上一篇文档中我们描述了 Android 启动中的 init 启动部分,本片文档将会继续 Android 启动流程的逻辑,继续梳理 Zygote 部分功能。 说明框架 对于 Zygote 进程,要从以下框架说明: 第一点,编译,zygo…...
2022NOIP比赛总结
种花 1.本题是一道前缀和优化加上枚举的问题。先考虑 C 因为 F 是 C 下边随便加一个点,所以只要求出 C 就求出了 F 。 注意到,并没有要求上下行一样,唯一的要求是 C 的两个横要隔一行,这就是问题的突破点,这题很明显…...

Leetcode 排序链表
这段代码的算法思想是 归并排序,一种适合链表的排序方法。它通过递归地将链表拆分成两部分,分别排序,然后合并已排序的部分,从而达到整体排序的目的。以下是代码的中文解释: 算法步骤: 找到链表的中点&…...

哈希函数简介
哈希函数是一种将任意大小的数据输入(通常称为“消息”)转换为固定大小的输出(称为“哈希值”或“摘要”)的算法。 主要特点: 1、输出固定长度 无论输入数据的大小如何,哈希函数的输出总是固定长度。例如…...

nginx------正向代理,反向代理生产,以及能否不使用代理详解
在生产环境中,选择使用正向代理还是反向代理取决于具体的应用场景和需求。下面详细解释这两种代理的用处以及为什么在不同情况下会选择它们。 正向代理 (Forward Proxy) 用途 匿名访问: 隐藏客户端的真实 IP 地址,提供隐私保护。常用于绕过…...
)
iptables限制docker端口禁止某台主机访问(使用DOCKER链和raw表的PREROUTING链)
背景: 在Linux上docker映射了端口,想着对服务端口进行限制指定IP访问,发现在filter表的INPUT链限制无效 环境: 主机192.168.56.132上的docker容器部署了nginx并将容器80端口映射到主机8000端口 [rootlocalhost ~]# docker ps …...

【VM实战】VMware迁移到VirtualBox
VMware 虚拟机开机卸载VMware Tools 调整虚拟磁盘 对于Windows 10及以上的虚拟机,一般VMware默认都会选Nvme固态硬盘。在导出前必须将其改为SATA,否则VirtualBox导入会报Appliance Import错误 (E_INVALIDARG 0x80070057) 先删掉当前盘的挂载ÿ…...

Android WebView加载不到cookie
以下配置根据需求酌情添加,建议逐个试验,cookie操作不是内存操作,建议修改配置后卸载app再重新运行防止缓存影响测试结果。 1.设置应用程序的 WebView 实例是否应发送并接受 Cookie CookieManager cookieManager CookieManager.getInstanc…...

c++qt
1.显示画布 #include "code.h" #include <QtWidgets/QApplication> #include<iostream> #include<vector> #include <QWindow> #include <QGraphicsView> #include <QGraphicsScene>using namespace std;//1.空格 2.墙 3.入口…...

零跑汽车嵌入式面试题汇总及参考答案
C++ 的三大特性是什么? C++ 的三大特性分别是封装、继承和多态。 封装 概念:封装是把数据和操作数据的函数绑定在一起,对数据的访问进行限制。通过将数据成员声明为私有或保护,只允许通过公共的成员函数来访问和修改数据,从而隐藏了类的内部实现细节。这有助于提高代码的安…...

LC:贪心题解
文章目录 376. 摆动序列 376. 摆动序列 题目链接:https://leetcode.cn/problems/wiggle-subsequence/description/ 这个题目自己首先想到的是动态规划解题,贪心解法真的非常妙,参考下面题解:https://leetcode.cn/problems/wiggle…...

ubuntu交叉编译dbus库给arm平台使用
1.下载dbus库源码 https://www.freedesktop.org/wiki/Software/dbus 克隆源码: https://gitlab.freedesktop.org/dbus/dbus/-/tree/dbus-1.12?ref_type=heads 下载1.12.20版本: 指定pkgconfig环境变量: export PKG_CONFIG_PATH=$PKG_CONFIG_PATH:$PWD/../expat-2.3.…...
ansible开局配置-openEuler
ansible干啥用的就不多介绍了,这篇文章主要在说ansible的安装、开局配置、免密登录。 ansible安装 查看系统版本 cat /etc/openEuler-latest输出内容如下: openeulerversionopenEuler-24.03-LTS compiletime2024-05-27-21-31-28 gccversion12.3.1-30.…...

连锁收银系统的优势与挑战
在快速发展的零售环境中,连锁收银系统不仅是收银的工具,更是现代零售管理的重要组成部分。它在提升效率、优化客户体验以及数据管理等方面发挥了关键作用。然而,随着技术的进步和市场环境的变化,连锁收银系统也面临着诸多挑战。本…...

轻型民用无人驾驶航空器安全操控理论培训知识总结-多旋翼部分
航空器知识 螺旋桨 螺旋桨为多旋翼民用无人驾驶航空器提供升力,多旋翼民用无人驾驶航空器通过飞控系统控制电机调节螺旋桨转速,来实现飞行。 天线 多旋翼民用无人驾驶航空器的图像传输以及遥控控制信号,主要是通过无线信道进行的,靠民用无人驾驶航空器与遥控器的天线传…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
