Linux find 匹配文件内容
在Linux中,你可以使用find命令结合-exec或者-exec+grep来查找匹配特定内容的文件。以下是一些示例:
查找当前目录及其子目录下所有文件内容中包含"exampleText"的文件:
find . -type f -exec grep -l "exampleText" {} \;查找/home目录下所有包含"exampleText"的文本文件:
find /home -type f -name "*.txt" -exec grep -l "exampleText" {} \;查找当前目录及子目录下所有.conf文件,并显示包含"ServerName"的文件及行:
find . -type f -name "*.conf" -exec grep "ServerName" {} \; -print 请注意,这些命令可能需要根据你的具体需求进行调整。例如,如果你需要区分大小写或者使用正则表达式,你可能需要调整grep命令的参数。
相关文章:

Linux find 匹配文件内容
在Linux中,你可以使用find命令结合-exec或者-execgrep来查找匹配特定内容的文件。以下是一些示例: 查找当前目录及其子目录下所有文件内容中包含"exampleText"的文件: find . -type f -exec grep -l "exampleText" {} \…...
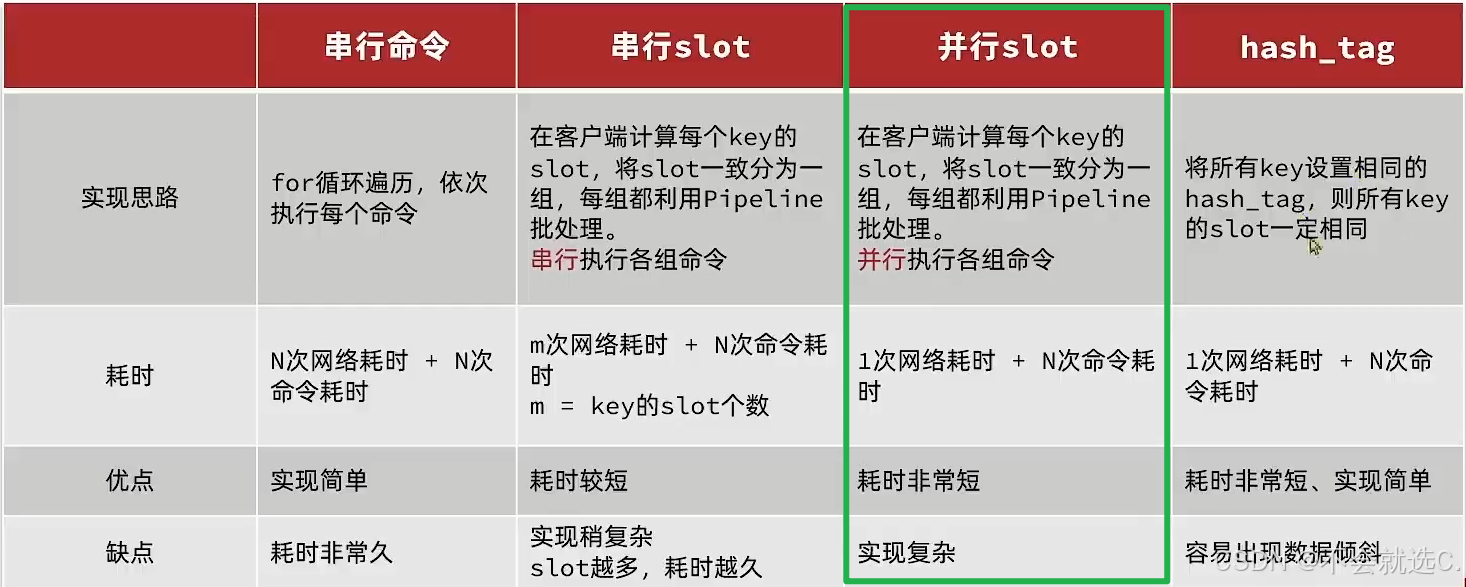
【Redis优化——如何优雅的设计key,优化BigKey,Pipeline批处理Key】
Redis优化——如何优雅的设计key,优化BigKey,Pipeline批处理Key 一、Key的设计1. 命名规范2. 长度限制在44字节以内 二、BigKey优化1. 查找bigkey2. 删除BigKey3. 优化BigKey 三、Pipeline批处理Key1. 单节点的Pipeline2. 集群下的Pipeline 一、Key的设计…...
数据结构与算法分析:你真的理解图算法吗——深度优先搜索(代码详解+万字长文)
一、前言 图是计算机科学中用来表示复杂结构信息的一种基本结构。本章我们会讨论一些通用的围表示法,以及一些频繁使用的图算法。本质上来说,一个图包含一个元素集合(也就是顶点),以及元素两两之间的关系(也就是边),由于应用范围所限,本章我们仅仅讨论简单图,简单围并不会如(a…...
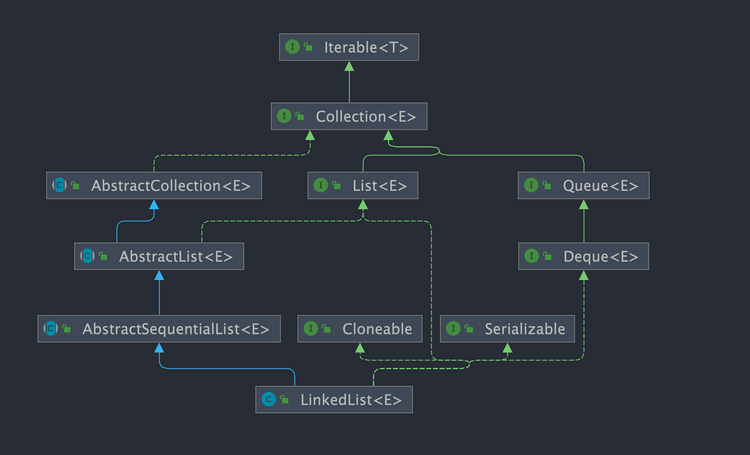
LinkedList 分析
LinkedList 简介 LinkedList 是一个基于双向链表实现的集合类,经常被拿来和 ArrayList 做比较。关于 LinkedList 和ArrayList的详细对比,我们 Java 集合常见面试题总结(上)有详细介绍到。 双向链表 不过,我们在项目中一般是不会使用到 Link…...
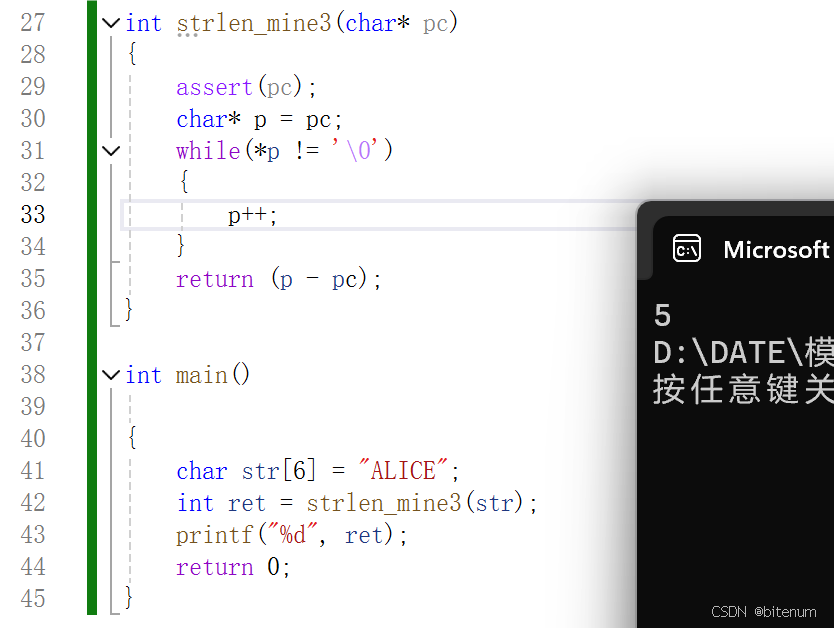
【C/C++】模拟实现strlen
学习目标: 使用代码模拟实现strlen。 逻辑: strlen 需要输入一个字符串数组类型的变量,并且返回一个整型类型的数据。strlen 需要计算字符串数组有多少个元素。 代码1:使用计数器 #define _CRT_SECURE_NO_WARNINGS 1 #include&…...
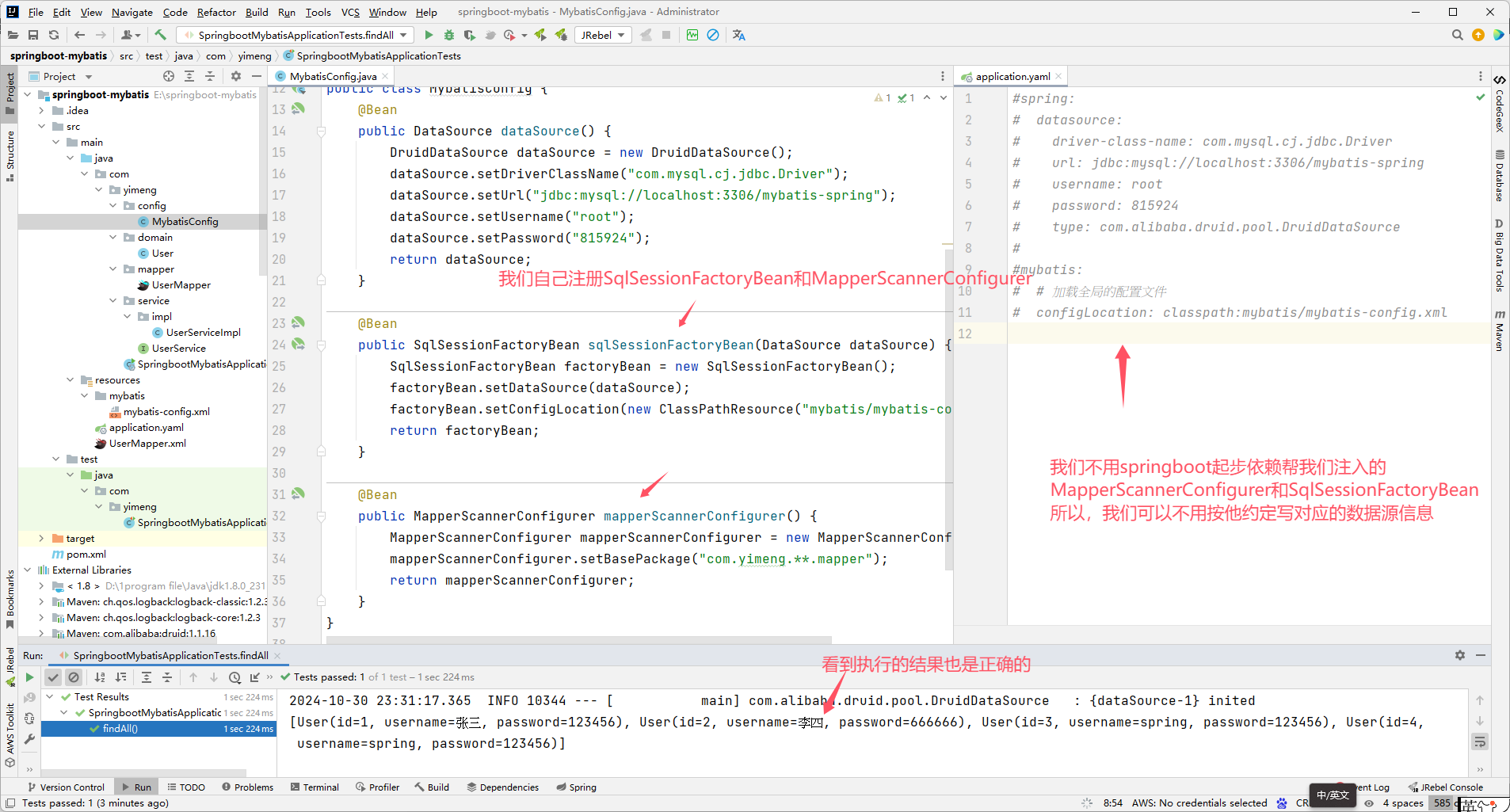
mybatis从浅入深一步步演变分析
mybatis从浅入深一步步演变分析 版本一:不使用代理(非spring) package com.yimeng.domain;public class User {private int id;private String username;private String password;public int getId() {return id;}public void setId(int id…...
Java阶段三02
第3章-第2节 一、知识点 面向接口编程、什么是spring、什么是IOC、IOC的使用、依赖注入 二、目标 了解什么是spring 理解IOC的思想和使用 了解IOC的bean的生命周期 理解什么是依赖注入 三、内容分析 重点 了解什么是spring 理解IOC的思想 掌握IOC的使用 难点 理解IO…...
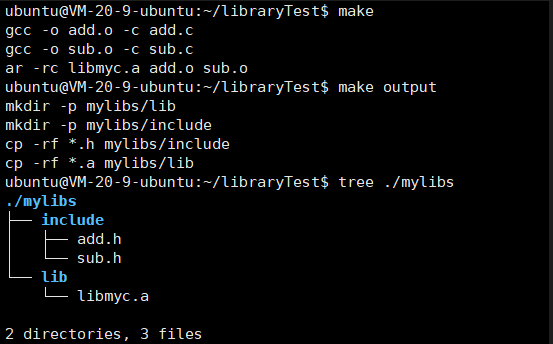
【Linux】掌握库的艺术:我的动静态库封装之旅
🌈个人主页:Yui_ 🌈Linux专栏:Linux 🌈C语言笔记专栏:C语言笔记 🌈数据结构专栏:数据结构 🌈C专栏:C 文章目录 1.什么是库1.2 认识动静态库1.2.1 动态库1.2.2…...
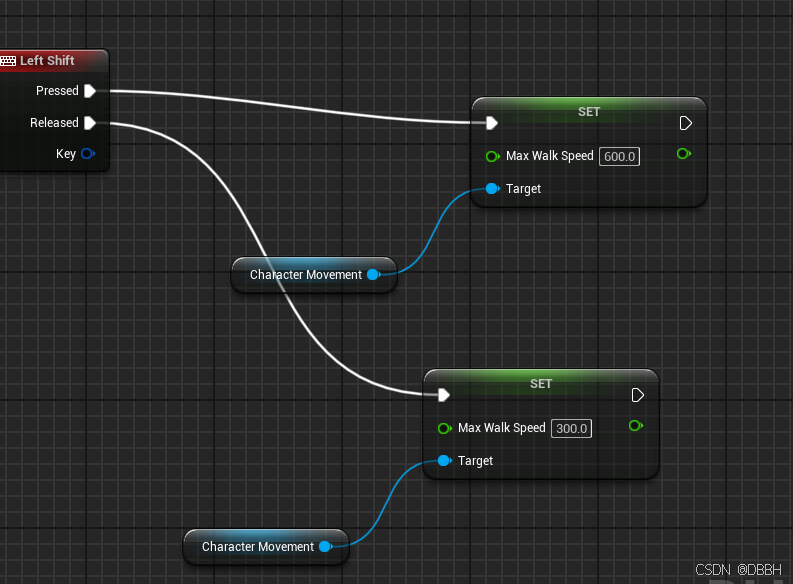
UE5动画控制 基础
素材 mixamo先去选择一个character 点击下载 就这个下载下来 然后选几个animation, 记得勾选 把动作下载了 without skin就是只要动作 然后把他们放在一个文件夹里先 UE里导入 找一个文件夹,直接拖拽进来那个character的fbx,默认配置就…...

流畅!HTMLCSS打造网格方块加载动画
效果演示 这个动画的效果是五个方块在网格中上下移动,模拟了一个连续的加载过程。每个方块的动画都是独立的,但是它们的时间间隔和路径被设计为相互协调,以创建出流畅的动画效果。 HTML <div class"loadingspinner"><…...

linux命令之top(Linux Command Top)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...
笔记)
数据结构-希尔排序(ShellSort)笔记
看动画理解 【数据结构】八大排序(超详解附动图源码)_数据结构排序-CSDN博客 一 基本思想 先选定一个整数gap,把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的元素进行排序。 然后将gap逐渐减小重复上…...

Junit + Mockito保姆级集成测试实践
一、做好单测,慢即是快 对于单元测试的看法,业界同仁理解多有不同,尤其是在业务变化快速的互联网行业,通常的问题主要有,必须要做吗?做到多少合适?现在没做不也挺好的吗?甚至一些大…...

软件项目管理要点
一.项目管理 1.盈亏平衡分析 销售额固定成本可变成本税费利润 当利润为0的时候就是盈亏平衡点。 2.范围管理 范围定义的输入包括:项目章程、项目范围管理计划、组织过程资产、批准的变更申请。 3.时间管理 项目时间管理中的过程包括活动定义、活动排序、活动的资…...

ESP8266 连接 MQTT 服务器EMQX 连接MQTTX
目录 1.先用有一台自己的云服务器 2. 使用FinalShell连接阿里云云服务器ECS 3.安装宝塔 4.在云服务器打开8888端口 5.使用外网面板地址打开宝塔面板 6.安装Docker 7.下载emqx 8.打开emqxWeb 界面 9.下载MQTTX 10.EMQX加一个客户端 11.开始通信 12.加入单片机ESP8266 …...

Python中如何处理异常情况?
1、Python中如何处理异常情况? 在Python中,处理异常情况通常使用try/except语句。try语句块包含可能会引发异常的代码,而except语句块包含处理异常的代码。如果try块中的代码引发了异常,控制流将立即转到相应的except块。 以下是…...

openpnp - 在openpnp中单独测试相机
文章目录 openpnp - 在openpnp中单独测试相机概述笔记END openpnp - 在openpnp中单独测试相机 概述 底部相机的位置不合适, 重新做了零件,准备先确定一下相机和吸嘴的距离是多少才合适。 如果在设备上直接实验,那么拆装调整相机挺麻烦的。 准备直接在电…...

Spark窗口函数
1、 Spark中的窗口函数 窗口就是单纯在行后面加一个列 可以套多个窗口函数,但彼此之间不能相互引用,是独立的 窗口函数会产生shuffle over就是用来划分窗口的 (1) 分组聚合里面的函数,基…...

Idea、VS Code 如何安装Fitten Code插件使用
博主主页:【南鸢1.0】 本文专栏:JAVA 目录 编辑 简介 所用工具 1、Idea如何安装插件 1.idea下载插件 2.需要从外部下载然后在安装, 2、VS Code如何安装插件 总结 简介 Fitten Code是由非十大模型驱动的AI编程助手,它可以自动生成代…...

elasticsearch7.x在k8s中的部署
一、说明 二、思路 三、部署 1、建nfs服务器 2、建持久卷 3、部署elasticsearch 四、附件 ?pv.yaml内容 elasticsearch.yaml内容 一、说明 本文章内容主要的参考来源是https://www.cnblogs.com/javashop-docs/p/12410845.html,但参考文献中的elasticsearc…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
