SMO算法 公式推导
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , N (9-69) \begin{aligned} & \min_{\alpha} \quad \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j K(x_i \cdot x_j) - \sum_{i=1}^{N} \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & \quad 0 \leq \alpha_i \leq C, \quad i = 1, 2, \cdots, N \tag{9-69} \end{aligned} αmin21i=1∑Nj=1∑NαiαjyiyjK(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=00≤αi≤C,i=1,2,⋯,N(9-69)
9.4.2 SMO 算法
SMO 算法主要用来求解式(9-69)的凸二次规划问题,在该问题中,变量是拉格朗日乘子 α i \alpha_i αi,一个 α i \alpha_i αi 对应一个样本点 ( x i , y i ) (x_i, y_i) (xi,yi),所以变量总数就是样本量 N N N。SMO 算法是一种针对非线性支持向量机凸优化问题快速求解的优化算法,其基本想法是:不断地将原二次规划问题分解为只有两个变量的子二次规划问题,并对该子问题进行解析和求解,直到所有变量都满足 KKT 条件为止。
假设选择的两个变量为 α 1 \alpha_1 α1 和 α 2 \alpha_2 α2, α 3 , α 4 , ⋯ , α N \alpha_3, \alpha_4, \cdots, \alpha_N α3,α4,⋯,αN 固定,那么式(9-69)的子问题可以表示为:
min α 1 , α 2 S ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K i 2 s.t. α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = γ 0 ≤ α i ≤ C , i = 1 , 2 (9-72) \begin{split} \min_{\alpha_1, \alpha_2} & \quad S(\alpha_1, \alpha_2) = \frac{1}{2} K_{11} \alpha_1^2 + \frac{1}{2} K_{22} \alpha_2^2 + y_1 y_2 K_{12} \alpha_1 \alpha_2 - (\alpha_1 + \alpha_2) + \\ & \quad y_1 \alpha_1 \sum_{i=3}^N y_i \alpha_i K_{i1} + y_2 \alpha_2 \sum_{i=3}^N y_i \alpha_i K_{i2} \\ \text{s.t.} & \quad \alpha_1 y_1 + \alpha_2 y_2 = -\sum_{i=3}^N y_i \alpha_i = \gamma \\ & \quad 0 \leq \alpha_i \leq C, \quad i = 1, 2 \tag{9-72} \end{split} α1,α2mins.t.S(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1α1i=3∑NyiαiKi1+y2α2i=3∑NyiαiKi2α1y1+α2y2=−i=3∑Nyiαi=γ0≤αi≤C,i=1,2(9-72)
其中 K i j = K ( x i , x j ) K_{ij} = K(x_i, x_j) Kij=K(xi,xj)。
式(9-72)即为两个变量的二次规划问题,先分析约束条件来考虑 α 2 \alpha_2 α2 的上下界问题。 α 1 \alpha_1 α1 和 α 2 \alpha_2 α2 都在 [ 0 , C ] [0, C] [0,C] 范围内,由式(9-72)的第一个约束条件可知, ( α 1 , α 2 ) (\alpha_1, \alpha_2) (α1,α2) 在平行于 [ 0 , C ] × [ 0 , C ] [0, C] \times [0, C] [0,C]×[0,C] 的对角线的直线上,如图 9-10 所示。

由图 9-10 可得 α 2 \alpha_2 α2 的上下界描述如下:当 y 1 ≠ y 2 y_1 \neq y_2 y1=y2 时,下界 L = max ( 0 , α 2 − α 1 ) L = \max(0, \alpha_2 - \alpha_1) L=max(0,α2−α1),上界 H = min ( C , C + α 2 − α 1 ) H = \min(C, C + \alpha_2 - \alpha_1) H=min(C,C+α2−α1);当 y 1 = y 2 y_1 = y_2 y1=y2 时,下界 L = max ( 0 , α 2 + α 1 − C ) L = \max(0, \alpha_2 + \alpha_1 - C) L=max(0,α2+α1−C),上界 H = min ( C , α 2 + α 1 ) H = \min(C, \alpha_2 + \alpha_1) H=min(C,α2+α1)。
下面对 α 1 \alpha_1 α1 和 α 2 \alpha_2 α2 求解进行简单推导。假设子问题式(9-72)的初始可行解为 α 1 old \alpha_1^\text{old} α1old 和 α 2 old \alpha_2^\text{old} α2old,最优解为 α 1 new \alpha_1^\text{new} α1new 和 α 2 new \alpha_2^\text{new} α2new,沿着约束方向上未经截断的 α 2 \alpha_2 α2 的最优解为 α 2 new, unc \alpha_2^\text{new, unc} α2new, unc。一般情况下,我们尝试首先沿着约束方向求未经截断即不考虑式(9-72)的第二个约束条件的最优解 α 2 new, unc \alpha_2^\text{new, unc} α2new, unc,然后再求截断后的最优解 α 2 new \alpha_2^\text{new} α2new。
令:
g ( x ) = ∑ i = 1 N α i y i K ( x i , x ) + b (9-73) g(x) = \sum_{i=1}^N \alpha_i y_i K(x_i, x) + b \tag{9-73} g(x)=i=1∑NαiyiK(xi,x)+b(9-73)
E i = g ( x i ) − y i = ( ∑ j = 1 N α j y j K ( x j , x i ) + b ) − y i (9-74) E_i = g(x_i) - y_i = \left( \sum_{j=1}^N \alpha_j y_j K(x_j, x_i) + b \right) - y_i \tag{9-74} Ei=g(xi)−yi=(j=1∑NαjyjK(xj,xi)+b)−yi(9-74)
当 i = 1 , 2 i = 1, 2 i=1,2 时, E i E_i Ei 为函数 g ( x ) g(x) g(x) 对输入 x i x_i xi 的预测值和真实值 y i y_i yi 之间的误差。
关于目标函数对 α 2 \alpha_2 α2 求偏导并令其为 0,可求得未经截断的 α 2 \alpha_2 α2 的最优解为:
α 2 new, unc = α 2 old + y 2 ( E 1 − E 2 ) κ (9-75) \alpha_2^\text{new, unc} = \alpha_2^\text{old} + \frac{y_2(E_1 - E_2)}{\kappa} \tag{9-75} α2new, unc=α2old+κy2(E1−E2)(9-75)
其中,
κ = K 11 + K 22 − 2 K 12 = ∥ ϕ ( x 1 ) − ϕ ( x 2 ) ∥ 2 (9-76) \kappa = K_{11} + K_{22} - 2K_{12} = \|\phi(x_1) - \phi(x_2)\|^2 \tag{9-76} κ=K11+K22−2K12=∥ϕ(x1)−ϕ(x2)∥2(9-76)
ϕ ( x ) \phi(x) ϕ(x) 为输入空间在特征空间中的映射。
经截断后的 α 2 \alpha_2 α2 可表示为:
α 2 new = { H , α 2 new, unc > H α 2 new, unc , L ≤ α 2 new, unc ≤ H L , α 2 new, unc < L (9-77) \alpha_2^\text{new} = \begin{cases} H, & \alpha_2^\text{new, unc} > H \\ \alpha_2^\text{new, unc}, & L \leq \alpha_2^\text{new, unc} \leq H \\ L, & \alpha_2^\text{new, unc} < L \tag{9-77} \end{cases} α2new=⎩ ⎨ ⎧H,α2new, unc,L,α2new, unc>HL≤α2new, unc≤Hα2new, unc<L(9-77)
接着基于 α 2 new \alpha_2^\text{new} α2new 可求得 α 1 new \alpha_1^\text{new} α1new:
α 1 new = α 1 old + y 1 y 2 ( α 2 old − α 2 new ) (9-78) \alpha_1^\text{new} = \alpha_1^\text{old} + y_1 y_2 \left( \alpha_2^\text{old} - \alpha_2^\text{new} \right) \tag{9-78} α1new=α1old+y1y2(α2old−α2new)(9-78)
最后,每次完成两个变量的优化后,还需要重新计算参数 b b b。 b b b 的计算分为四种情况:
当 0 < α 1 new < C 0 < \alpha_1^\text{new} < C 0<α1new<C 时,由:
∑ i = 1 N α i y i K i 1 + b = y 1 (9-79) \sum_{i=1}^N \alpha_i y_i K_{i1} + b = y_1 \tag{9-79} i=1∑NαiyiKi1+b=y1(9-79)
可得:
b 1 new = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 new y 1 K 11 − α 2 new y 2 K 21 (9-80) b_1^\text{new} = y_1 - \sum_{i=3}^N \alpha_i y_i K_{i1} - \alpha_1^\text{new} y_1 K_{11} - \alpha_2^\text{new} y_2 K_{21} \tag{9-80} b1new=y1−i=3∑NαiyiKi1−α1newy1K11−α2newy2K21(9-80)
同样,当 0 < α 2 new < C 0 < \alpha_2^\text{new} < C 0<α2new<C 时,有:
b 2 new = y 2 − ∑ i = 3 N α i y i K i 1 − α 2 new y 2 K 22 − α 1 new y 1 K 12 (9-81) b_2^\text{new} = y_2 - \sum_{i=3}^N \alpha_i y_i K_{i1} - \alpha_2^\text{new} y_2 K_{22} - \alpha_1^\text{new} y_1 K_{12} \tag{9-81} b2new=y2−i=3∑NαiyiKi1−α2newy2K22−α1newy1K12(9-81)
当 α 1 new \alpha_1^\text{new} α1new 和 α 2 new \alpha_2^\text{new} α2new 同时满足 0 < α 1 new < C 0 < \alpha_1^\text{new} < C 0<α1new<C 时,有:
b 1 new = b 2 new (9-82) b_1^\text{new} = b_2^\text{new} \tag{9-82} b1new=b2new(9-82)
最后一种情况是, α 1 new \alpha_1^\text{new} α1new 和 α 2 new \alpha_2^\text{new} α2new 都不在 [ 0 , C ] [0, C] [0,C] 范围内, b 1 new b_1^\text{new} b1new 和 b 2 new b_2^\text{new} b2new 都满足 KKT 条件,直接对其取均值即可。
综上,参数 b b b 可计算归纳为:
b new = { b 1 new , 0 < α 1 new < C b 2 new , 0 < α 2 new < C b 1 new + b 2 new 2 , 其他 (9-83) b^\text{new} = \begin{cases} b_1^\text{new}, & 0 < \alpha_1^\text{new} < C \\ b_2^\text{new}, & 0 < \alpha_2^\text{new} < C \\ \frac{b_1^\text{new} + b_2^\text{new}}{2}, & 其他 \end{cases} \tag{9-83} bnew=⎩ ⎨ ⎧b1new,b2new,2b1new+b2new,0<α1new<C0<α2new<C其他(9-83)
以下是本文部分公式的详细解释:
公式9-72
拉格朗日乘子上界和下界
公式9-78
相关文章:

SMO算法 公式推导
min α 1 2 ∑ i 1 N ∑ j 1 N α i α j y i y j K ( x i ⋅ x j ) − ∑ i 1 N α i s.t. ∑ i 1 N α i y i 0 0 ≤ α i ≤ C , i 1 , 2 , ⋯ , N (9-69) \begin{aligned} & \min_{\alpha} \quad \frac{1}{2} \sum_{i1}^{N} \sum_{j1}^{N} \alpha_i \alpha_j…...

nodejs包管理器pnpm
简介 通常在nodejs项目中我们使用npm或者yarn做为默认的包管理器,但是pnpm的出现让我们的包管理器有了更多的选择,pnpm相比npm具有以下优势: 速度更快,pnpm在安装依赖时,会将依赖包缓存到全局目录,下次安…...
【postman】工具下载安装
postman作用 postman用于测试http协议接口,无论是开发, 还是测试人员, 都有必要学习使用postman来测试接口, 用起来非常方便。 环境安装 postman 可以直接在chrome 上安装插件,当然大部分的同学是没法连接到谷歌商店的,我们可以在电脑本地…...

Java_Springboot核心配置详解
Spring Boot以其简洁、高效和约定优于配置的理念,极大地简化了Java应用的开发流程。在Spring Boot中,核心配置是应用启动和运行的基础。本文将详细介绍Spring Boot中的两种配置文件格式、基础注解的配置方式、自定义配置以及多环境配置。 一、Spring Bo…...
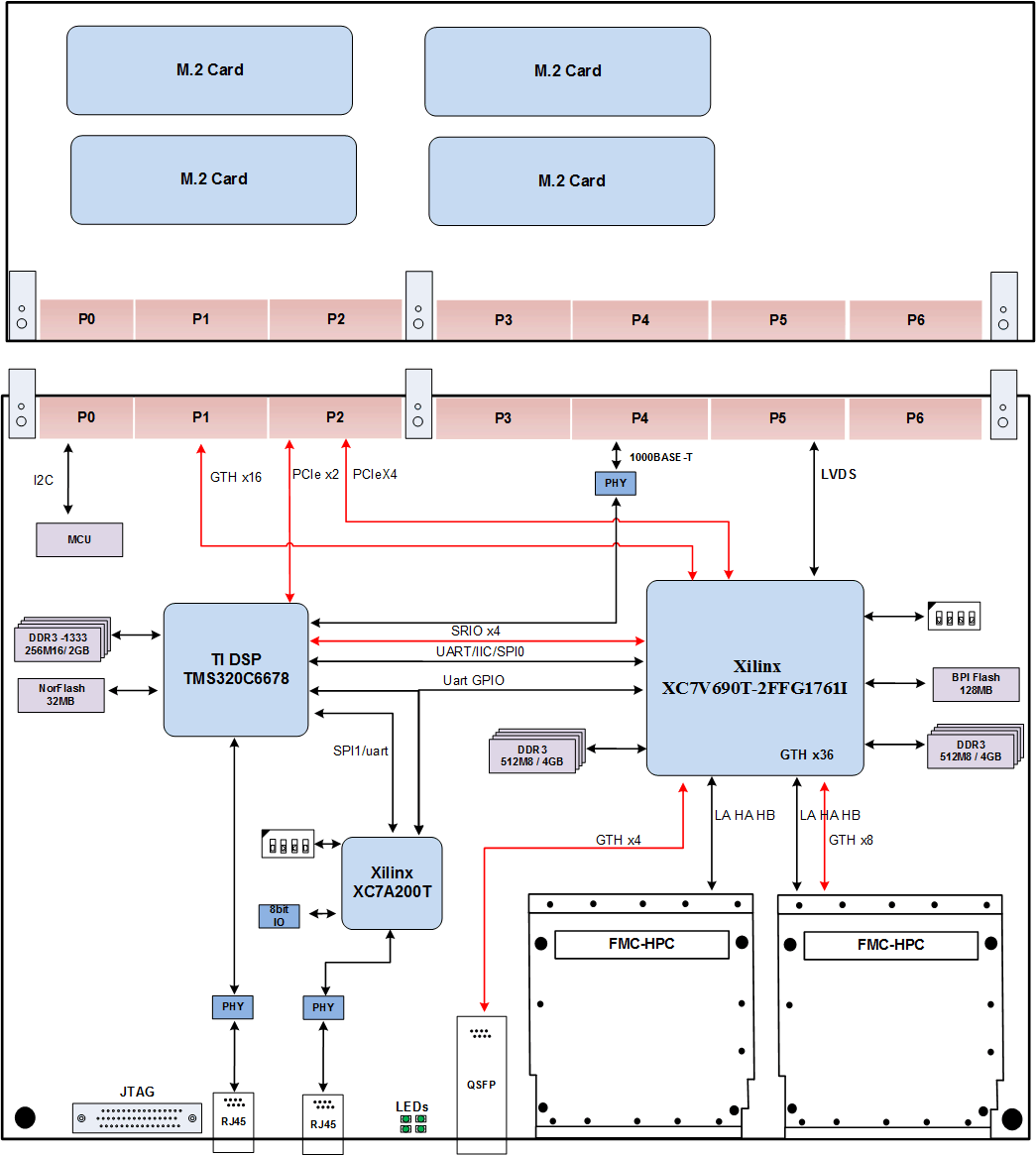
太速科技-9-基于DSP TMS320C6678+FPGA XC7V690T的6U VPX信号处理卡
基于DSP TMS320C6678FPGA XC7V690T的6U VPX信号处理卡 一、概述 本板卡基于标准6U VPX 架构,为通用高性能信号处理平台,系我公司自主研发。板卡采用一片TI DSP TMS320C6678和一片Xilinx公司Virtex 7系列的FPGA XC7V690T-2FFG1761I作为主处理器&#…...
在线UI设计工具:创意与效率的结合
随着UI设计领域的快速增长,设计师们纷纷投身于这一行业,选择一款合适的UI设计工具变得至关重要。除了经典的UI设计软件,在线UI设计工具因其灵活性和便捷性,越来越受到设计师们的喜爱。这种不受时间和地点限制,且不依赖…...
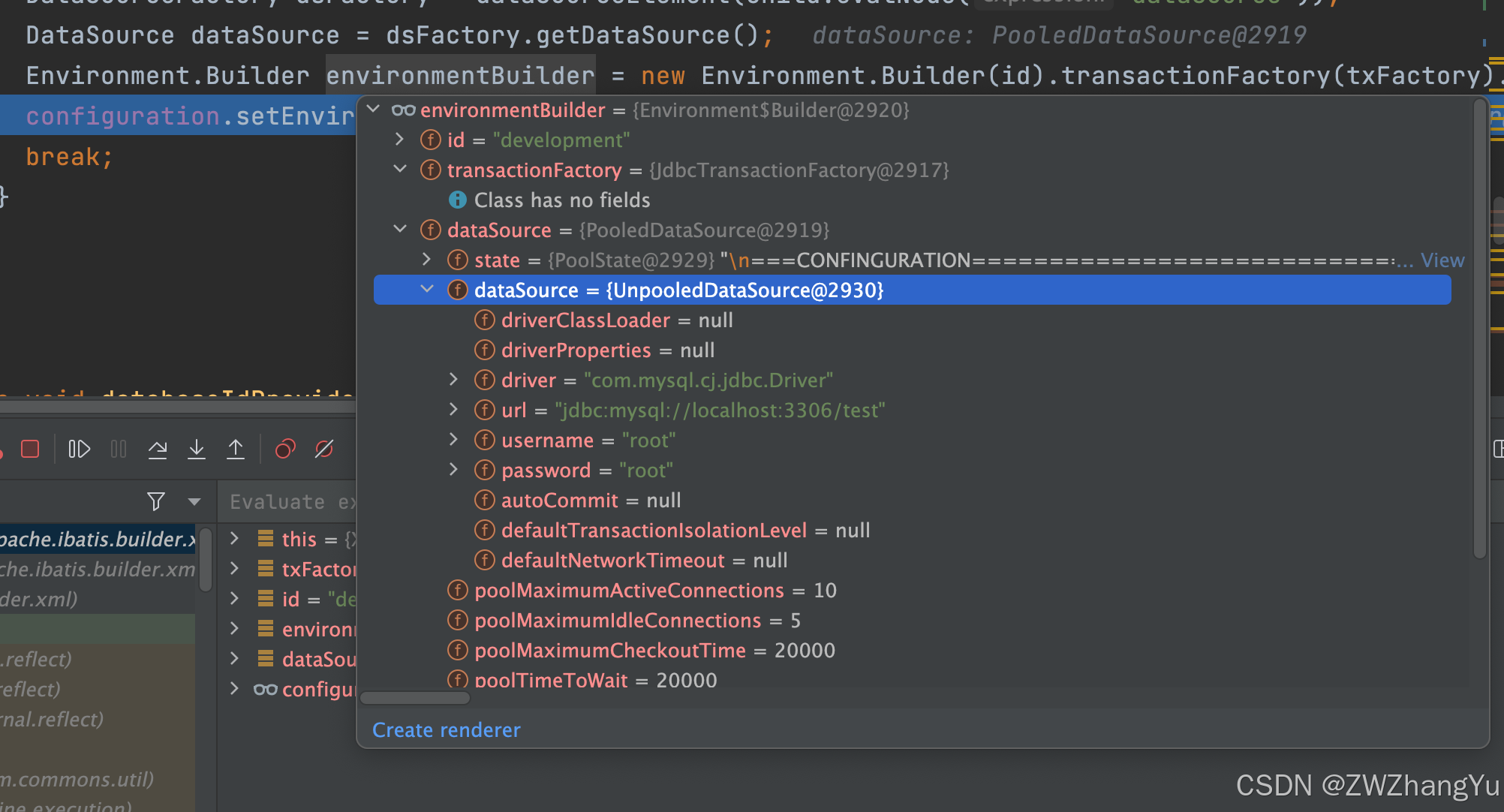
【MyBatis源码】SqlSessionFactoryBuilder源码分析
文章目录 概述类结构从 InputStream 创建 SqlSessionFactoryXMLConfigBuilder构建ConfigurationXMLConfigBuilder初始化方法parse()方法parseConfiguration属性(properties) 概述 SqlSessionFactory 是 MyBatis 的核心接口之一,提供创建 Sql…...

Percona XtraBackup数据备份方案
一、简介 官方文档:https://docs.percona.com/percona-xtrabackup/innovation-release/index.html Percona XtraBackup 是一款适用于基于 MySQL 的服务器的开源热备份实用程序,可让您的数据库在计划的维护时段内保持完全可用。无论是 24x7 高负载服务器还是低交易量服务器,…...

聚“芯”而行,华普微亮相第五届Silicon Labs Works With大会
2024年10月24日,由致力于以安全、智能无线连接技术建立更互联世界的全球领导厂商Silicon Labs主办的第五届Works With开发者大会在上海雅乐居万豪侯爵酒店成功举办。 作为全球性的物联网年度“盛宴”,本届大会群英荟萃,不仅有着来自生态大厂的…...

Java 用户随机选择导入ZIP文件,解压内部word模板并入库,Windows/可视化Linux系统某麒麟国防系统...均可适配
1.效果 压缩包内部文件 2.依赖 <!--支持Zip--><dependency><groupId>net.lingala.zip4j</groupId><artifactId>zip4j</artifactId><version>2.11.5</version></dependency>总之是要File类变MultipartFile类型的 好像是…...

【C++】C++17结构化绑定、std::optional、std::variant、std::any
二十二、C17中的结构化绑定、std::optional、std::variant、std::any 本部分是一个小系列,介绍C17中新引入的、用来解决各种不同返回情况的、标准库新组件。 1、C的结构化绑定 结构化绑定structured bindings是C17中引入的一项特性,它允许开发者方便地…...

C#的起源。J++语言的由来?J#和J++傻傻分不清?
C#的起源 C#读音是C Sharp, 它是微软为了对抗Java而生,最早是J,效率比Java还好,后来被Sun公司起诉J破坏了平台无关性,微软重新开发C#. C#和Java一样都定位为中间件语言,用虚拟机执行编译的字节码以达到跨平台目的。从语…...

Flutter 在 对接 google play 时,利用 android studio 可视化生成 已签名的aab包
android studio 可视化生成 aab包 第一 : 先说注意事项 在Flutter项目里面,直接打开当前项目是不行的,不显示相应操作,需要在Android 目录打开,直白点就是直接打开项目里面的Android 目录 不然会出现的一些问题 第一…...

使用web.dev提供的工具实现浏览器消息推送服务
文章目录 前言实现工具和效果实现原理实现过程前端接收用户订阅请求将用户订阅信息更新到后端后端实现接收并保存订阅信息的接口后端实现消息推送的逻辑前言 对于电商独立站来说,新品上架或者促销活动上线及时通知到用户是很重要的,通知的渠道有很多,其中就包括浏览器消息推…...

计算机系统结构为什么用architecture 而不是structure?
architecture本意是建筑学、建筑艺术,其含义就是建筑的样子和背后的设计思想,用于计算机科学可以表达计算机的系统结构和后面的设计原理:它长什么样?它为什么长这样? 与architecture 对应的词是structure (…...

sqoop问题汇总记录
此篇博客仅记录在使用sqoop时遇到的各种问题。持续更新,有问题评论区一起探讨,写得有不足之处见谅。 Oracle_to_hive 1. main ERROR Could not register mbeans java.security.AccessControlException: access denied ("javax.management.MBeanTr…...

Git 创建新的分支但清空提交记录
有时候需要创建新的分支,但是原有分支的提交非常多,不好区分哪些是创建分支之后的提交。 那么就把原分支的提交全部去掉 要从 分支1 创建 分支2,并确保 分支2 不包含任何提交历史,同时文件与 分支1 的最后一次提交一致࿰…...

SQL PRIMARY KEY
SQL PRIMARY KEY 概述 在关系型数据库中,主键(PRIMARY KEY)是一个非常重要的概念。它是表中每一行数据的唯一标识符,用于保证数据的完整性和准确性。本文将详细介绍SQL中的主键,包括其定义、作用、如何创建和修改主键…...

软件测试学习笔记丨Flask操作数据库-对象与数据模型
本文转自测试人社区,原文链接:https://ceshiren.com/t/topic/23440 对象与数据模型 数据模型:是数据特征的抽象,抽象层次上描述了系统的静态特征、动态行为和约束条件,为数据库系统的信息表示与操作提供一个抽象的框架…...

IntelliJ IDEA使用 MybatisX-Generator 插件 自动生成Entity+Mapper+Mapper.xml等代码
一、Intellij安装MybatisX插件: 首先点击 Intellij->Preference->Plugins,然后搜索MybatisX,点击安装: 2 打开数据库 在IntelliJ IDEA 连接Mysql数据库,选择表,点击右键,选择 Mybatis…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
