[POI2014] PTA-Little Bird(单调队列优化 DP)
luogu 传送门![]() https://www.luogu.com.cn/problem/P3572
https://www.luogu.com.cn/problem/P3572
解题思路
先设 表示到
的最小劳累值。
很容易得出转移:
其中 由
和
的大小关系决定,并且
。
很显然,直接暴力是 的,会超时。
于是,考虑优化。
我们发现 是有一定的取值范围,并且我们取的是这个区间内的最小值。
也许这可以用单调队列优化。
判断对头是否在范围内,如果不在即出队;
入队的时候,考虑队尾的劳累值是否大于当前的劳累值,如果大于,则队尾出队,如果队尾的劳累值等于当前的劳累值,我们可以比较谁的高度更高,保留更高的(因为更高的对后面的情况更优)。
于是,时间复杂度降为
代码
#include<bits/stdc++.h>
using namespace std;int n;
int d[1000001];
int qi;
int ki;
int f[1000001];
int q[1000001];
int head,tail;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>d[i];}cin>>qi;while(qi--){cin>>ki;head=1,tail=0;f[1]=0;q[++tail]=1;for(int i=2;i<=n;i++){while(head<=tail&&q[head]<i-ki)head++;if(d[i]>=d[q[head]])f[i]=f[q[head]]+1;elsef[i]=f[q[head]];while(head<=tail&&(f[q[tail]]>f[i]||(f[q[tail]]==f[i]&&d[q[tail]]<=d[i])))tail--;q[++tail]=i;} cout<<f[n]<<endl;}return 0;
}相关文章:
[POI2014] PTA-Little Bird(单调队列优化 DP)
luogu 传送门https://www.luogu.com.cn/problem/P3572 解题思路 先设 表示到 的最小劳累值。 很容易得出转移: 其中 由 和 的大小关系决定,并且 。 很显然,直接暴力是 的,会超时。 于是,考虑优化。 我们发现…...
【含开题报告+文档+PPT+源码】基于SpringBoot的体育馆管理系统的设计与实现
开题报告 近年来,随着人们生活水平的提高和健康意识的增强,体育馆作为提供体育锻和休闲娱乐的重要场所,其使用频率和管理难度也在不断增加。传统的体育馆管理模式通常依赖于人工记录和手动操作,不仅效率低下,而且容易…...

Vue3学习:vue组件中的图片路径问题
今天在做一个案例的时候,图片放在assets/images文件夹下,如下路径,其中的图片不能正常显示。 list: [{ id: 1, name: 欧拉公式啤酒杯, price: 30.00, src: ./assets/images/Euler.png},{ id: 2, name: 高斯分布马克杯, price: 40.00, src: ./…...

openCV基础-图像预处理Day26
图像预处理 在计算机视觉和图像处理领域,图像预处理是一个重要的步骤,它能够提高后续处理(如特征提取、目标检测等)的准确性和效率。OpenCV 提供了许多图像预处理的函数和方法,以下是一些常见的图像预处理操作&…...

给文件添加可读可写可执行权限
在Unix、Linux或类Unix操作系统中,你可以使用chmod命令来给文件添加可读、可写和可执行权限。权限通常分为三组:文件所有者(owner)、文件所属组(group)和其他用户(others)。每组都可…...

golang有序map
最近使用go开发排行榜的需求, 有些情况会用到有序map, 但是go竟然没有有序map的实现 本着自己动手丰衣足食的原则, 就自己实现了一个 原理 原理比较简单, 主要结合了container/list双向链表和map 使用双向链表存储key和value, 保证顺序, 使用map存储key和节点信息, 保证查找…...

【LangChain系列4】【Chain模块详解】
目录 前言一、LangChain1-1、介绍1-2、LangChain抽象出来的核心模块1-3、特点1-4、langchain解决的一些行业痛点1-5、安装 二、Chain模块2-1、介绍2-2、LLMChain2-3、Sequential Chain(顺序链)2-4、Router Chain 总结 前言 LangChain给自身的定位是&…...
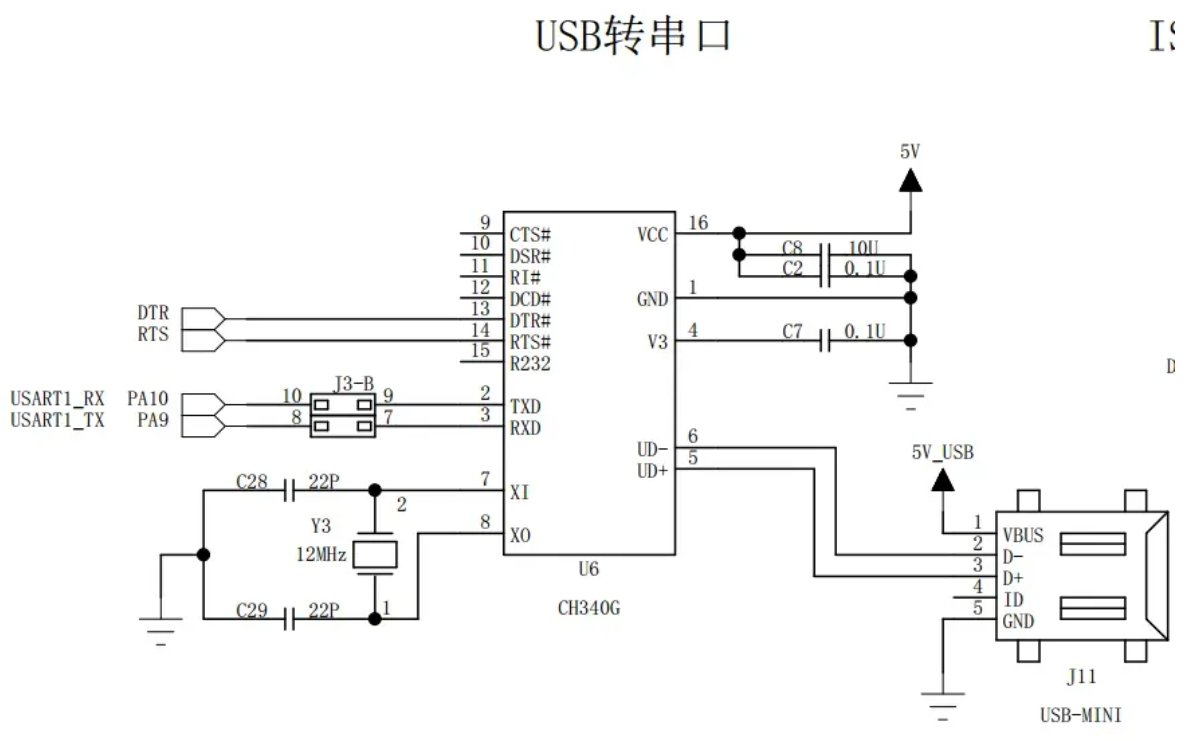
51c嵌入式~IO合集1
我自己的原文哦~ https://blog.51cto.com/whaosoft/12383193 一、单片机通信数据接收解析方法 前阵子一朋友使用单片机与某外设进行通信时,外设返回的是一堆格式如下的数据: AA AA 04 80 02 00 02 7B AA AA 04 80 02 00 08 75 AA AA 04 80 02 00 9B E2…...

ETLCloud怎么样?深度解析其在数据管理中的表现
在BI或数据大屏等数据分析工具中,经常需要从多个业务系统中提取原始数据,然后对数据进行清洗、处理,以获取高质量、有效且干净的数据以供后续的BI进行数据统计和分析使用,从高质量的实现企业数据的价值变现。 然而,在…...

高频谐振功放电路
目录 集电极馈电电路 高频扼流圈的作用: 并联馈电回路 高频扼流圈作用 : 优缺点 对于并联的集电极馈电网络: 对于串联的集电极馈电网络: 神奇之处 基级馈电电路 自反偏压: 复合输出回路 天线回路 效率分析 总效率分析 互感如何改变工作状态 集电极馈电电路 馈电电路分…...

kafka如何获取 topic 主题的列表?
大家好,我是锋哥。今天分享关于【kafka如何获取 topic 主题的列表?】面试题?希望对大家有帮助; kafka如何获取 topic 主题的列表? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在Kafka中,可以…...

全新大模型框架Haystack,搭建RAG pipeline
大家好,在AI应用开发的赛道上,目前Haystack以其开源框架的优势,成为LLM技术领域的一匹黑马,对现有竞争者构成挑战。本文将介绍Haystack的亮点优势,并分析它为何能在众多LLM框架中脱颖而出,通过RAG应用实例来…...

儿童孤独症专家分享:了解治疗与支持的专业帮助
在儿童的成长旅程中,每一步都充满了探索与发现。然而,对于患有孤独症的儿童来说,这段旅程往往伴随着更多的挑战与困难。孤独症,这个看似遥远的词汇,却深刻地影响着无数家庭的生活。作为儿童孤独症领域的专家࿰…...

初始JavaEE篇——多线程(7):定时器、CAS
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程程(ಥ_ಥ)-CSDN博客 所属专栏:JavaEE 目录 定时器的使用 定时器的原理 模拟实现定时器 CAS 介绍 CAS的应用场景 解析 AtomicInteger 类 实现自旋锁 CAS的缺陷…...

高精度计算(乘)
引言 此篇是专栏信息学杂谈第八篇高精度计算(乘),展示了关于C如何实现高精度乘法的代码 正文: 乘法进位 c[i j - 1] a[i] * b[j] x; //x为之前进位 x c[i j - 1] / 10; c[i j - 1] % 10;完整代码: #include …...

在vue中 如何实现跨域
跨域问题是Web开发中常见的挑战,那么如何解决跨域呢,我们一起来看看吧! 跨域是什么? 跨域(Cross-Origin)是指网络请求从一个域名(origin)发起,而请求的目标资源位于另一…...

计算机考研,选择西安交通大学还是哈工大?
C哥专业提供——计软考研院校选择分析专业课备考指南规划 经过全面分析,2025年考研西安交通大学和哈尔滨工业大学计算机专业的报考难度对比如下: 西安交通大学计算机专业 > 哈尔滨工业大学计算机专业 对于想要报考985高校计算机专业但核心目标是优…...

微积分复习笔记 Calculus Volume 1 - 4.4 The Mean Value Theorem
4.4 The Mean Value Theorem - Calculus Volume 1 | OpenStax...

Cpp多态机制的深入理解(20)
文章目录 前言一、多态的概念二、多态的定义与实现两个必要条件虚函数虚函数的重写重写的三个例外override 和 final重载、重写(覆盖)、重定义(隐藏) 三、抽象类概念接口继承和实现继承 四、多态的原理虚表和虚表指针虚函数调用过程动态绑定与静态绑定 五、那...那单继承甚至多…...

(六)Python结构数据类型
一、集合类型(Sets) Sets(集合)是一个无序不重复的元素集。主要功能是自动清除重复的元素。创建集合时使用大括号{}包含其中元素。 Food{西瓜,南瓜,冬瓜,北瓜} print(Food) 输出结果: 增加重复元素,则会…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
