了解神经网络中的激活函数
一、激活函数的特征
- 非线性,激活函数必须是非线性函数。
- 可微性,训练网络模型时,基于梯度的模型最优化方法要求激活函数必须是可导的。
- 单调性,单调递增或单调递减,单调函数保证模型的简单。
- 隐藏层一般需要使用激活函数已引入非线性,输入层不需要。输出层如果是回归问题也是不需要的,如果是多分类问题,使用softmax函数将输出转化为概率分布,如果是二分类问题,可以使用sigmoid函数。
二、常见的激活函数
-
sigmoid函数
sigmoid激活函数: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1,其导数为: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x)),导数的取值范围[0, 1/4],sigmoid在使用反向传播来训练神经网络时,会产生梯度消失的问题,另外sigmoid处理后的输出数据是一个非负值,在反向传播过程中会增加梯度的不稳定性。
-
tanh函数
tanh激活函数: f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x,其导数为: f ′ ( x ) = 1 − f ( x ) 2 f'(x)=1-f(x)^2 f′(x)=1−f(x)2,导数的取值范围为[0, 1],反向传播过程中衰减速度比sigmoid要慢,经过tanh激活函数处理后的输出均值约为0(这相当于做了归一化),所以tanh比sigmoid具有更稳定的梯度,但是依然无法避免梯度消失的问题。
-
近似生物神经元的激活函数
如ReLU,softplus等,还有Leaky ReLU,ELU,Softmax等。
三、常见的神经网络模型
| 神经网络类型 | 主要特点 | 典型应用场景 |
|---|---|---|
| 前馈神经网络 | 信息单向流动,无反馈循环;层级结构清晰;常用于分类和回归问题 | 图像分类、文本分类、回归预测 |
| 反馈神经网络(RNN) | 信息可以在网络中循环传播,具有记忆能力;适用于序列数据 | 自然语言处理(机器翻译、情感分析)、语音识别、时间序列预测 |
| 卷积神经网络(CNN) | 利用卷积核提取局部特征,适用于图像、视频等数据 | 图像分类、目标检测、图像分割 |
| 循环神经网络变种(LSTM、GRU) | 改进RNN,解决了长期依赖问题,更好地处理长序列数据 | 自然语言处理、语音识别 |
| 生成对抗网络(GAN) | 由生成器和判别器组成,通过对抗学习生成新的数据 | 图像生成、数据增强 |
| 图神经网络(GNN) | 处理图结构数据,适用于社交网络、分子结构等 | 社交网络分析、药物发现 |
相关文章:

了解神经网络中的激活函数
一、激活函数的特征 非线性,激活函数必须是非线性函数。可微性,训练网络模型时,基于梯度的模型最优化方法要求激活函数必须是可导的。单调性,单调递增或单调递减,单调函数保证模型的简单。隐藏层一般需要使用激活函数…...
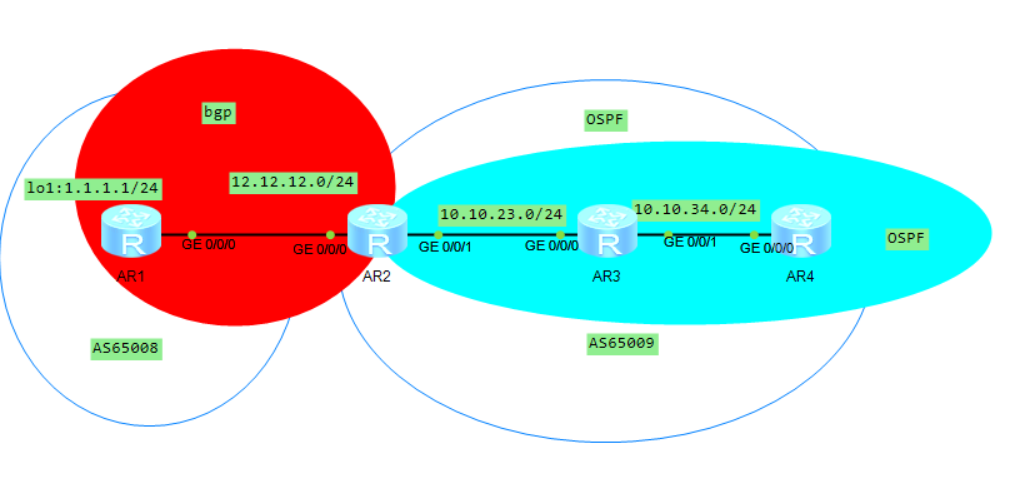
配置BGP与IGP交互和路由自动聚合示例
组网需求 如图所示,用户将网络划分为AS65008和AS65009,在AS65009内,使用IGP协议来计算路由(该例使用OSPF做为IGP协议)。要求实现两个AS之间的互相通信。 配置思路 采用如下的思路配置BGP与IGP交互: 在AR…...

代码随想录算法训练营第三十三天 | 62.不同路径 63.不同路径
LeetCode 62.不同路径: 文章链接 题目链接:62.不同路径 思路: 动态规划 使用二维数组保存递推结果 ① dp数组及下标含义 dp[i][j]:表明从(0, 0)到下标为(i, j)的点有多少条不同的路径 ② 递推式: 机器人只能向下或向…...

使用Flask构建RESTful API
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用Flask构建RESTful API Flask简介 环境搭建 安装Flask 项目结构 创建应用 路由定义 请求处理 获取查询参数 获取请求体 响应…...

基于springboot的Java学习论坛平台
基于springboot的Java学习论坛平台 摘 要 在Internet高速发展的今天,我们生活的各个领域都涉及到计算机的应用,其中包括学习平台的网络应用,在外国学习平台已经是很普遍的方式,不过国内的管理平台可能还处于起步阶段。学习平台具…...

Python离线环境搭建
引言 在软件开发过程中,我们常常会遇到内网环境无法直接访问外网的情况,这就需要我们通过一些特殊手段来搭建Python开发环境。本文将详细介绍如何利用U盘在内网机与外网机之间迁移Python环境及其依赖包。 工具准备 1台内网机1台外网机1个U盘 操作步骤…...

windows下kafka使用出现的问题
kafka启动 启动kafka需要先启动zookeeper,在kafka根目录下先启动zookeeper .\bin\windows\zookeeper-server-start.bat .\config\zookeeper.properties启动kafka 另开一个cmd命令行 .\bin\windows\kafka-server-start.bat .\config\server.propertieskafka与jdk版…...

ctfshow文件包含web78~81
目录 web78 方法一:filter伪协议 方法二:input协议 方法三:data协议 web79 方法一:input协议 方法二:data协议 web80 方法一:input协议 方法二:日志包含getshell web81 web78 if(isset($_GET[file]…...

鸿蒙生态认识
好的,让我们更深入地探讨鸿蒙生态的发展机遇、面临的挑战,以及未来的潜力。 对鸿蒙生态的认知与分析 鸿蒙系统作为一种新兴的操作系统,旨在打破设备之间的壁垒,打造一个更加连通的生态环境。以下是对其崛起的进一步分析…...

Hadoop-004-Big Data Tools插件的使用
一、Big Data Tools插件配置流程 1、安装Big Data Tools插件 以IntelliJ IDEA 2024.2.3为例打开setting, 搜索安装Big Data Tools插件后重启IDEA 2、Windows系统基础配置 Windows系统需要做一些基础设置,配合插件使用,将之前下载的hadoop-3.2.4.tar.gz 解压到D…...

linux8在线扩容/home目录
虚机新增1T磁盘 [rootrsb ~]# cat /etc/redhat-release Red Hat Enterprise Linux release 8.8 (Ootpa) [rootrsb ~]# vgs VG #PV #LV #SN Attr VSize VFree ol 2 3 0 wz--n- <2.00t 0 [rootrsb ~]# lvs LV VG Attr LSize Pool Origin Dat…...

【C/C++】模拟实现strcpy
学习目标: 使用代码模拟实现strcpy。 逻辑: strcpy 函数的返回类型是 void 即不返回数据。strcpy 函数的参数类型是 char* ,用于接收数组。strcpy 函数要把一个数组复制到另一个数组。 代码: #define _CRT_SECURE_NO_WARNINGS …...

网络编程番外——IO多路复用的应用说明
一、IO多路复用与多线程 IO多路复用,IO Multiplexing,其实就是在IO上进行监听处理导致线程被阻塞(如果非阻塞就必须不断的轮询,仍然是占用此线程),如果一个IO对应一个线程是不是太浪费了。而且在诸如网络I…...

【Java爬虫的淘宝寻宝记】—— 淘宝商品类目的“藏宝图”
引言: 在淘宝这个广袤的“商品宇宙”中,每一件商品都是一颗璀璨的星球,而商品类目就是连接这些星球的星际航道。今天,我们将派遣一位勇敢的Java爬虫宇航员,去揭开这些星际航道背后的秘密——商品类目。准备好了吗&…...

探索Python文档自动化的奥秘:揭开docxtpl库的神秘面纱
文章目录 探索Python文档自动化的奥秘:揭开docxtpl库的神秘面纱1. 背景介绍2. 库简介3. 安装指南4. 基础函数介绍5. 实际应用场景6. 常见问题及解决方案7. 总结 探索Python文档自动化的奥秘:揭开docxtpl库的神秘面纱 1. 背景介绍 在日常工作中…...

RabbitMQ的解耦、异步、削峰是什么?
RabbitMQ在分布式系统和微服务架构中起到了重要的作用,其特性可以实现解耦、异步以及削峰,下面是对这三个概念的详细解释: 1. 解耦 解耦是指使系统的不同组件间的依赖关系减少或消失。在使用RabbitMQ时,生产者(发送消…...
4:arm汇编语言4:bits/byte的介绍(ASCII码)与二进制补位
4.2 bits/byte的介绍与ASCII码的引入 这个是详细介绍计算机内部原理的基础,bits与byte其实这两个是计算机中非常重要的单位。首先看一下bits,它是一个基础的计算机单位。计算机单位?像长度单位是米,体重的单位是kg,你…...

C++实现仿安卓线程Handler、Message、Looper的功能
在java开发中,习惯使用Handler、Message来处理同步,比如对相机的操作(open、setParamters、start、stop、clost)全部抛到同一个线程处理,防止并发操作导致异常,这样保留给外部的统一接口就是安全的,无论外部哪些线程来…...

构建安全的用户登录API:从请求验证到JWT令牌生成
构建安全的用户登录API:从请求验证到JWT令牌生成 为了实现这个后端POST /api/users/login端点,我们可以使用Node.js和Express框架,并结合一些常用的库如jsonwebtoken、bcrypt和express-validator来处理验证和密码校验。下面是一个完整的示例…...

状态模式:封装对象状态并改变行为的设计模式
1. 引言 在软件开发中,某些对象的行为会随着其内部状态的变化而变化。传统的实现方式可能需要使用大量的条件语句,导致代码复杂且难以维护。状态模式(State Pattern)提供了一种有效的方法,通过将状态行为封装在状态类…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
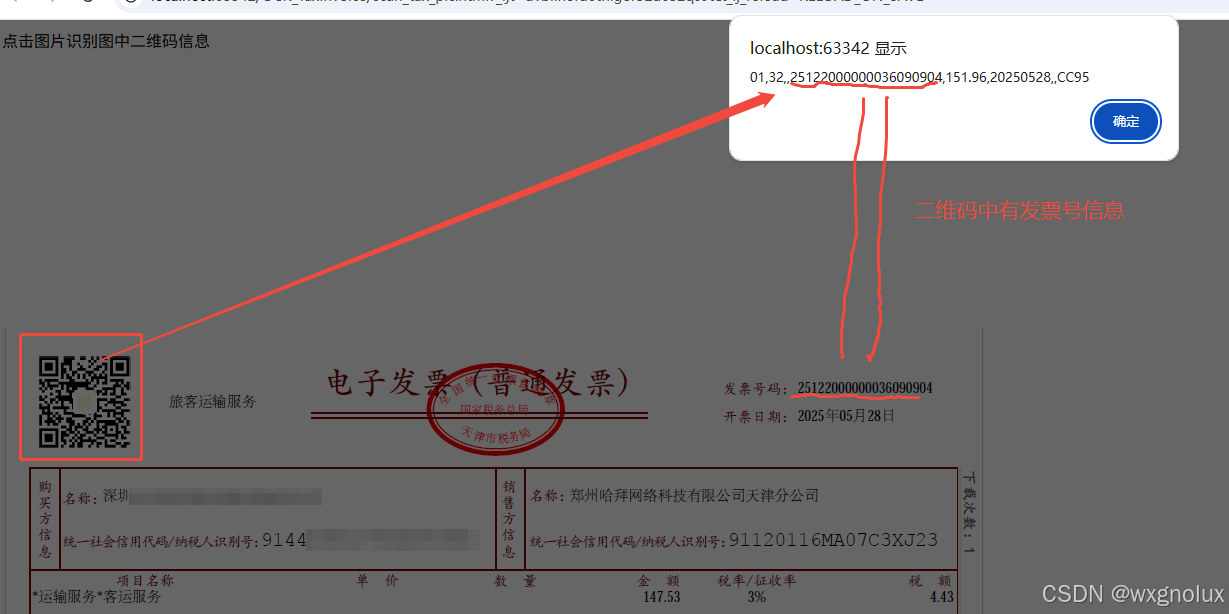
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
