xmuoj [蒙德里安的梦想] 状压dp个人笔记

本题是状压dp经典题目,很多人都是通过这一题开始对状压dp有所了解。
在进行讲解之前,我们先通过几个问答大致了解状压dp。
一、问答
1. 问题:什么是状压dp?
回答:状压dp即为状态压缩动态规划,何为状态压缩?怎么进行状态压缩?是个问题。
这个问题涉及到了状压dp的核心思想——把问题的状态压缩成整数,因为整数便于存储和进行状态转移。
2. 问题:状压dp状态的存储形式是?
回答:前面已经说了,问题的状态应该压缩成整数,但是单纯的10进制整数显然无法满足最小子问题的状态存储,或者说,浪费了很多存储空间。对于最小子问题,一般情况下,只有 1 和 0 两种状态,那么,我们用二进制存储显然更优。
3. 问题:用二进制存储状态只是存储上更优吗?
回答:不然,二进制天然的位运算可以大大加速状态转移。这也是状压dp不会超时的重要原因。
哈哈,关键词get到了吗?二进制、位运算 ✿✿ヽ(°▽°)ノ✿
二、下面进行例题讲解
错误思路我就不讲了,因为错误思路千奇百怪,我也是开始就想偏了(我上来就是dp[n][m]一顿转移)。
首先,我们应该明白的是,我们只能放横着放或者竖着放长方形,一旦横着放的确定了(横着的放法要在合理情况下,总不能让竖的放不了吧O(∩_∩)O ),那么竖着的一定就只有一种可能了,所以,我们只需考虑横着放有多少种合理的放法即可。

下面该怎么做呢?已经焦头烂额了,开始吟唱
对于第 i 列,我们假设 0~ i -1 列的横着放的长方形已经全部放好了,我们都知道,横着放的一定有突出的部分。

就比如说,对于这张图,第 i 列突出的部分是 0、1、3这三个位置,用二进制表示即为101100,对应十进制的44,所以,这个状态就是 f [ i ][ 44 ]
不难发现,第 i 列状态是由第 i-1 列的状态转移过来的
具体来说,f [ i ][ j ] +=所有满足条件的 f[ i-1][ k ]
要满足什么条件呢?
1. j 和 k不能重叠(显然长方形不能重叠放置,可以重叠的话放法就无穷尽了)
 对于这个条件,保证 j&k==0 即可
对于这个条件,保证 j&k==0 即可
2. j和k放完之后,第i-1列不能有连续奇数个0(因为这样就放不了竖着的了)

定义isok[ i ]表示 i 的二进制表示是否满足上述条件,isok[ i ] = true表示满足条件,
保证 isok[ j | k ]为 true 即可
三、C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;
bool isok[M];
long long f[N][M];
int main() {while (cin >> n >> m, n || m) {for (int i = 0;i < 1<<n;i++) {//计算isok[i]isok[i] = true;int cnt = 0;for (int j = 0;j < n;j++) {if (i >> j & 1) {if (cnt % 2)isok[i] = false;cnt = 0;}else cnt++;}if (cnt % 2)isok[i] = false;}memset(f, 0, sizeof f);f[0][0] = 1;for (int i = 1;i <=m;i++) {for (int j = 0;j < 1<<n;j++) {for (int k = 0;k < 1<<n;k++) {if (isok[j | k] && !(j & k)) {//满足两个条件才能转移f[i][j] += f[i - 1][k];}}}}cout << f[m][0] << endl;//代表到 m列且没有突出的情况(列数为0~m-1,m列表示遍历完成了)}return 0;
}四、结尾
写完再回首,不禁又感叹状压dp的巧妙,如此优雅,妙哉妙哉。
这就是今天要分享的内容,感谢观看!
相关文章:

xmuoj [蒙德里安的梦想] 状压dp个人笔记
本题是状压dp经典题目,很多人都是通过这一题开始对状压dp有所了解。 在进行讲解之前,我们先通过几个问答大致了解状压dp。 一、问答 1. 问题:什么是状压dp? 回答:状压dp即为状态压缩动态规划,何为状态压缩&#x…...

ubuntu22安装搜狗输入法不能输入中文
关闭Wayland 在/etc/gdm3/custom.conf文件内,取消注释WaylandEnable cat /etc/gdm3/custom.conf | grep WaylandEnable WaylandEnablefalse 其它步骤参考搜狗官方教程 https://pinyin.sogou.com/linux/help.php...

HtmlAgilityPack 操作详解
目录 1.安装 HtmlAgilityPack 2. 示例 HTML 3. 使用 HtmlAgilityPack 进行 HTML 解析与操作 4. 代码详解 1.加载html文档 2.选择元素 3. 提取属性 4.修改属性 5.常用的几种获取元素的 XPath 写法 HtmlAgilityPack: 轻量且高效,适合进行常规的 H…...

基于SSM医院门诊互联电子病历管理系统的设计
管理员账户功能包括:系统首页,个人中心,用户管理,医生管理,项目分类管理,项目信息管理,预约信息管理,检查信息管理,系统管理 用户账号功能包括:系统首页&…...
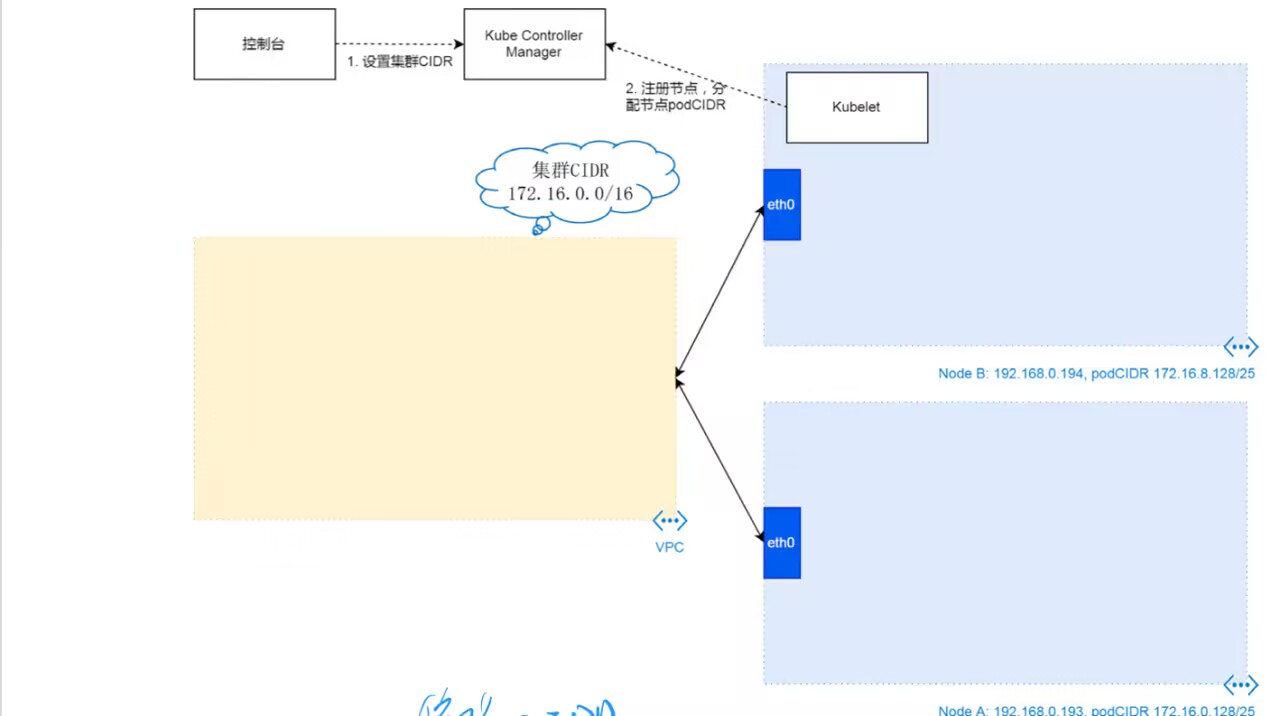
【读书笔记/深入理解K8S】集群网络
前言 上一章讲了集群控制器的一个大概的原理,这一章讲一下集群网络。网络是集群通信的载体,因为该书是阿里云团队出品的,所以也以阿里云的集群网络方案为例,其他云厂商的网络集群方案一般来说也大同小异。所以通过本章的学习&…...
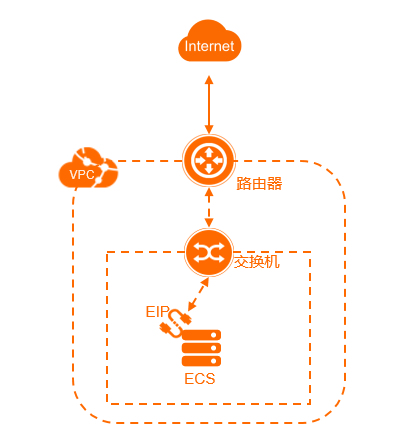
【专有网络VPC】连接公网
通过ECS实例固定公网IP、弹性公网IP、NAT网关、负载均衡使专有网络中的云资源可以访问公网(Internet)或被公网访问。 概述 专有网络是您自定义的云上私有网络。专有网络中的云资源默认无法访问公网,也无法被公网访问。您可以通过配置ECS实例…...

论文 | Legal Prompt Engineering for Multilingual Legal Judgement Prediction
这篇文章探讨了如何利用“法律提示工程”(LPE)来指导大型语言模型(LLM)进行多语言法律判决预测(LJP)。主要内容: LPE 的概念: LPE 是指通过设计特定的提示(promp…...

国科安芯抗辐照MCU和CANFD芯片发布
国科安芯科技有限公司近期发布了两款重要的芯片产品:抗辐照MCU芯片和抗辐照CANFD芯片。这两款芯片的发布标志着国科安芯在高性能、高安全性芯片产品研制方面取得了显著进展,特别是在抗辐照技术领域。 1. 抗辐照MCU芯片:国科安芯研发的AS32A4…...
)
C++ 并发专题 - 无锁数据结构(概述)
一:概述: 无锁数据结构是一种在多线程环境中实现线程安全的结构,它允许多个线程在没有传统锁机制的情况下并发访问和修改数据。这种设计的目标是提高程序的性能和响应性,避免锁竞争和上下文切换的开销。 二:原理&…...

NLP领域的经典算法和模型
在自然语言处理(NLP)领域,经典算法和模型众多,它们在不同任务中发挥着重要作用。以下是一些NLP领域的经典算法和模型的详细介绍: 一、基础模型 词袋模型(Bag of Words,BoW) 原理&a…...

提升安全上网体验:Windows 11 启用 DOH(阿里公共DNS)
文章目录 阿里公共 DNS 介绍免费开通云解析 DNS 服务Windows 编辑 DNS 设置配置 IPv4配置 IPv6 路由器配置 DNS 阿里公共 DNS 介绍 https://alidns.com/ 免费开通云解析 DNS 服务 https://dnsnext.console.aliyun.com/pubDNS 开通服务后,获取 DOH 模板࿰…...

论文概览 |《Journal of Transport Geography》2024.10 Vol.120
本次给大家整理的是《Journal of Transport Geography》杂志2024年9月第120卷的论文的题目和摘要,一共包括17篇SCI论文! 论文1 Modelling scenarios in planning for future employment growth in Stockholm 斯德哥尔摩未来就业增长规划情景建模 【摘要…...

yum不能使用: cannot find a valid baseurl for repo: base/7/x86_64
使用yum命令时报错: 原因: CentOS 已经停止维护的问题。2020 年 12 月 8 号,CentOS 官方宣布了停止维护 CentOS Linux 的计划,并推出了 CentOS Stream 项目,CentOS Linux 8 作为 RHEL 8 的复刻版本,生命周期…...

什么品牌的护眼台灯比较好?五款护眼效果比较明显的护眼台灯
在当今信息爆炸的时代背景下,挑选一款真正符合个人需求的护眼台灯,确实是一项不小的挑战。市场上品牌众多、型号繁杂,功能特点各不相同,价格区间也相当广泛,许多消费者在选购时往往感到迷茫不已。当大家询问“什么品牌…...

HTML 表单设计与验证
创建 HTML 表单的步骤如下: 使用 <form> 标签来创建表单,<form> 标签有一个 action 属性,用于指定表单提交的目标 URL。 在 <form> 标签内部,使用 <input> 标签来创建输入框。<input> 标签有一个 …...

qt QDialog详解
1、概述 QDialog是Qt框架中用于创建对话框的类,它继承自QWidget。QDialog提供了一个模态或非模态的对话框,用于与用户进行交互。模态对话框会阻塞其他窗口的输入,直到用户关闭该对话框;而非模态对话框则允许用户同时与多个窗口进…...

supervisor服务“Exited too quickly“解决方案
【初始问题】supervisor创建一个守护进程,老是提示启动失败 【结论】进程执行后,短时间就断开了 Ⅰ 问题分析 supervisor开启进程守护失败了,查看下进程执行记录,显示这个进程的指令执行报错了 接下来,查看下superv…...

动态规划 —— 路径问题-地下城游戏
1. 地下城游戏 题目链接: 174. 地下城游戏 - 力扣(LeetCode)https://leetcode.cn/problems/dungeon-game/description/ 2. 算法原理 状态表示:以莫一个位置位置为结尾或者以莫一个位置为起点 dp[i,j]表示:…...

沈阳乐晟睿浩科技有限公司抖音小店短视频时代的电商蓝海
在数字化浪潮席卷全球的今天,电子商务以其独特的魅力和无限的潜力,成为了推动经济发展的新引擎。作为这一领域的佼佼者,沈阳乐晟睿浩科技有限公司凭借其深厚的行业积淀与创新精神,正逐步成为众多商家在抖音小店平台上腾飞的强大助…...

ubuntu20.04安装ros与rosdep
目录 前置配置 配置apt清华源 配置ros软件源 添加ros安装源(中科大软件源) 设置秘钥 更新源 ros安装 安装ros 初始化 rosdep 更新 rosdep 设置环境变量 安装 rosinstall 安装验证 启动海龟仿真器 操控海龟仿真器 rosdep安装更新 安装 使用…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
