diffusion model 学习笔记
条件引导的 diffusion
对于无条件的DDPM 而言
p ( x t ∣ x 0 ) ∼ N ( α t ˉ x 0 , 1 − α t ˉ ⋅ I ) p(x_t | x_0) \sim \mathcal{N}( \sqrt{\bar{\alpha_t}} x_0, 1-\bar{\alpha_t} \cdot \mathrm{I} ) p(xt∣x0)∼N(αtˉx0,1−αtˉ⋅I)
可以得到
log p ( x t ∣ x 0 ) = − 1 2 ( x t − α t ˉ x 0 ) 2 1 − α t ˉ \begin{aligned} \log p(x_t|x_0) &= - \frac{1}{2} \frac{ (x_t - \sqrt{\bar{\alpha_t}} x_0) ^ 2 }{ 1-\bar{\alpha_t} } \end{aligned} logp(xt∣x0)=−211−αtˉ(xt−αtˉx0)2
计算其 score func, 可以得到
∇ x log p ( x t ∣ x 0 ) = − ( x t − α t ˉ x 0 ) 1 − α t ˉ = − ϵ 1 − α t ˉ ≈ − ϵ θ ( x t , t ) 1 − α t ˉ \begin{aligned} \nabla_x \log p(x_t|x_0) &= -\frac{ (x_t - \sqrt{\bar{\alpha_t}} x_0) }{ 1-\bar{\alpha_t} } \\ &= -\frac{ \epsilon } { \sqrt{1-\bar{\alpha_t}} } \\ & \approx -\frac{ \epsilon_{\theta}(x_t, t) }{ \sqrt{1-\bar{\alpha_t}} } \end{aligned} ∇xlogp(xt∣x0)=−1−αtˉ(xt−αtˉx0)=−1−αtˉϵ≈−1−αtˉϵθ(xt,t)
也就是,我们训练的网络conditionalUnet 输出的是噪声的估计, 这个估计的噪声 ϵ θ ( x t , t ) \epsilon_{\theta}(x_t, t) ϵθ(xt,t)可以用来计算当前数据点在整个概率空间中的score-func: ∇ x log p ( x t ∣ x 0 ) \nabla_x \log p(x_t|x_0) ∇xlogp(xt∣x0).
对于 conditional Diffusion. 其 score func 可以写成
∇ x t log p ( x t ∣ y ) = ∇ x t log ( p ( x t ) ⋅ p ( y ∣ x t ) p ( y ) ) = ∇ x t log p ( x t ) + ∇ x t log p ( y ∣ x t ) − ∇ x t log p ( y ) ⏟ = 0 和 x t 无关 = ∇ x t log p ( x t ) ⏟ u n c o n d i t i o n a l s c o r e + ∇ x t log p ( y ∣ x t ) ⏟ a d v e r s i a l g r a d i e n t \begin{aligned} \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log \left ( \frac{ p(x_t) \cdot p(y|x_t) }{ p(y) } \right) \\ &= \nabla_{x_t} \log p(x_t) + \nabla_{x_t} \log p(y|x_t) - \underbrace{\nabla_{x_t} \log p(y)} _{=0 \ \ 和 x_t 无关} \\ &= \underbrace{ \nabla_{x_t} \log p(x_t)}_{ \mathrm{unconditional\ score} } + \underbrace{ \nabla_{x_t} \log p(y|x_t) }_{ \mathrm{adversial\ gradient} } \end{aligned} ∇xtlogp(xt∣y)=∇xtlog(p(y)p(xt)⋅p(y∣xt))=∇xtlogp(xt)+∇xtlogp(y∣xt)−=0 和xt无关 ∇xtlogp(y)=unconditional score ∇xtlogp(xt)+adversial gradient ∇xtlogp(y∣xt)
现在,我们需要估计 ∇ x t log p ( x t ∣ y ) \nabla_{x_t} \log p(x_t|y) ∇xtlogp(xt∣y) 中的 ϵ ′ \epsilon' ϵ′, 然后使用 DDPM/DDIM 采样即可. 不妨设
∇ x t log p ( x t ∣ y ) = − ϵ ′ 1 − α t ˉ \begin{align} \nabla_{x_t} \log p(x_t|y) &= -\frac{ \epsilon' }{ \sqrt{ 1- \bar{\alpha_t}} } \end{align} ∇xtlogp(xt∣y)=−1−αtˉϵ′
则我们有
∇ x t log p ( x t ∣ y ) = ∇ x t log p ( x t ) + ∇ x t log p ( y ∣ x t ) ⏟ 令 = g − ϵ ′ 1 − α t ˉ = − ϵ 1 − α t ˉ + g 可得 : ϵ ′ = ϵ − 1 − α ˉ t ⋅ g \begin{align} \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log p(x_t) + \underbrace{ \nabla_{x_t} \log p(y|x_t)}_{ 令 = g } \\ -\frac{ \epsilon' }{ \sqrt{ 1- \bar{\alpha_t}} } &= -\frac{ \epsilon }{ \sqrt{ 1- \bar{\alpha_t}} } + g \\ 可得 &: \epsilon' = \epsilon - \sqrt{1-\bar{\alpha}_t} \cdot g \end{align} ∇xtlogp(xt∣y)−1−αtˉϵ′可得=∇xtlogp(xt)+令=g ∇xtlogp(y∣xt)=−1−αtˉϵ+g:ϵ′=ϵ−1−αˉt⋅g
即我们在无条件模型 DDPM 估计的噪声中添加一个微小的扰动( 1 − α ˉ t ⋅ g \sqrt{1-\bar{\alpha}_t}\cdot g 1−αˉt⋅g),就可以作为条件模型的噪声估计.
-
g = ∇ x t log p ( y ∣ x t ) g = \nabla_{x_t} \log p(y|x_t) g=∇xtlogp(y∣xt) 的含义:
条件概率的梯度: ∇ x t log p ( y ∣ x t ) \nabla_{x_t} \log p(y|x_t) ∇xtlogp(y∣xt) 表示的是在已知 x t x_t xt的情况下,微小变化 x t x_t xt如何影响条件 y y y的对数概率。这是一个 向量场,指向增加条件 y y y出现概率的方向。
-
如何得到
g假设我现在已经有了一个回归模型, 即 y = f ( x t , . . . ) y = f(x_t, ...) y=f(xt,...).
输入一个数据 x t x_t xt, 返回其对应一个 logit 值.
## 输入: x_t, 模型 f x_t = torch.tensor(x_t, requires_grad=True) y = f(x_y) ## pytorch model 预测其结果 log_p = torch.log(y) ## 计算 log 概率 log_p.backward() ## 计算梯度 grad_x_t = x_t.grad ## 获取梯度
Langevin Dynamics 采样
首先,假设我们已经有了一个训练好的score-func( s θ ( x ) s_{\theta}(x) sθ(x)). 已经接近于真实的 s ( x ) s(x) s(x), 即 s θ ( x ) = ∇ x log p θ ( x ) s_{\theta}(x)=\nabla_{x} \log p_{\theta}(x) sθ(x)=∇xlogpθ(x), 其中 p θ ( x ) ≈ p ( x ) p_{\theta}(x) \approx p(x) pθ(x)≈p(x). 现在, 我们需要利用 s θ ( x ) s_{\theta}(x) sθ(x) 对 x 进行采样,使得 x ∼ p θ ( x ) x \sim p_{\theta}(x) x∼pθ(x)
郎之万公式: 描述了粒子做随机布朗运动 (粒子位置随时间变化的关系), 是一种 SDE, 描述了 由梯度力(即. U ( x ( t ) U(x(t) U(x(t))驱动并受到随机噪声(即. Z t Z_t Zt)影响的系统的时间演化.
d X ( t ) = − ∇ x U ( x ( t ) ) ⋅ d t + σ d t ⋅ Z t dX(t) = -\nabla_x U(x(t)) \cdot dt + \sigma \sqrt{dt} \cdot Z_t dX(t)=−∇xU(x(t))⋅dt+σdt⋅Zt
X ( t ) X(t) X(t):
Diffuser 源码解读
DDPMSchedule
1. α , α ˉ , β \alpha, \bar{\alpha}, \beta α,αˉ,β 的关系和计算
x t = α t ⋅ x t − 1 + 1 − α t ⋅ ϵ t = ∏ i = 1 t α i ⋅ x 0 + 1 − ∏ i = 1 t α i ⋅ ϵ 0 = α t ˉ ⋅ x 0 + 1 − α t ˉ ⋅ ϵ 0 β t = 1 − α t \begin{align} x_t &= \sqrt{\alpha_t} \cdot x_{t-1} + \sqrt{ 1-\alpha_t } \cdot \epsilon_t \\ &= \sqrt{\prod_{i=1}^{t} \alpha_i } \cdot x_0 + \sqrt{1-\prod_{i=1}^{t}\alpha_i} \cdot \epsilon_0 \\ &= \sqrt{\bar{\alpha_t}} \cdot x_0 + \sqrt{1-\bar{\alpha_t}} \cdot \epsilon_0 \\ \beta_t &= 1-\alpha_t \end{align} xtβt=αt⋅xt−1+1−αt⋅ϵt=i=1∏tαi⋅x0+1−i=1∏tαi⋅ϵ0=αtˉ⋅x0+1−αtˉ⋅ϵ0=1−αt
-
在
DDPMSchedule中, 先计算出 β t \beta_t βt 的值,然后利用 α t = 1 − β t \alpha_t = 1- \beta_t αt=1−βt 计算剩下的系数。 -
self.beta的计算有各种不同的方法,- trained_betas: 需要传入自定义的beta
- linear
- squaredcos_cap_v2
- …
-
alpha和alpha_cumprod的计算self.alphas = 1.0 - self.betas self.alphas_cumprod = torch.cumprod(self.alphas, dim=0) # 累积乘积(cumulative product) -
self.betas: 是扩散过程中“噪声量”的度量。控制着每一步扩散过程中加入的噪声量的大小. -
self.alphas: 每一步中保留的原始信号的比例。
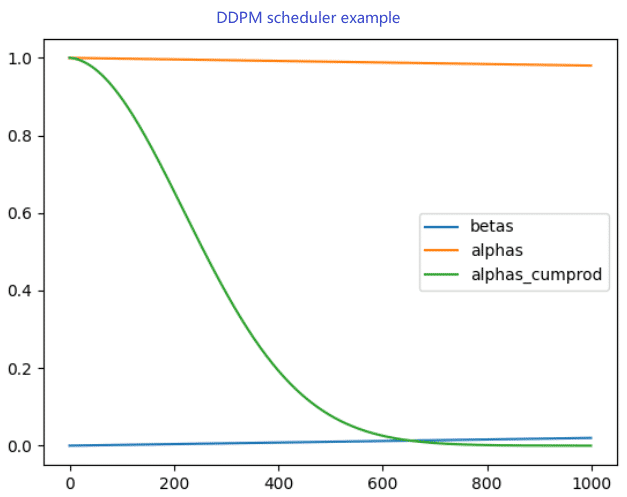
上图是 DDPM 中的 α \alpha α, β \beta β, α ˉ \bar{\alpha} αˉ 的关系。
2. 计算前向时刻的采样: x t → x t − 1 x_t \rightarrow x_{t-1} xt→xt−1
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) N ( x t − 1 ; α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) ∝ N ( x t − 1 ; α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t ⏟ μ q ( x t , x 0 ) , ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I ⏟ Σ q ( t ) ) \begin{align} q(x_{t-1}|x_t, x_0) &= \frac{ q(x_t|x_{t-1}, x_0) q(x_{t-1}|x_0) }{ q(x_t|x_0) }\\ &= \frac{\mathcal{N}(x_{t} ; \sqrt{\alpha_t} x_{t-1}, (1 - \alpha_t)\textbf{I})\mathcal{N}(x_{t-1} ; \sqrt{\bar\alpha_{t-1}}x_0, (1 - \bar\alpha_{t-1}) \textbf{I})}{\mathcal{N}(x_{t} ; \sqrt{\bar\alpha_{t}}x_0, (1 - \bar\alpha_{t})\textbf{I})} \\ &\propto \mathcal{N}( x_{t-1} ; \underbrace{\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}}}_{\mu_q(x_t, x_0)}, \underbrace{\frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}}\textbf{I}}_{{\Sigma}_q(t)}) \end{align} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)=N(xt;αˉtx0,(1−αˉt)I)N(xt;αtxt−1,(1−αt)I)N(xt−1;αˉt−1x0,(1−αˉt−1)I)∝N(xt−1;μq(xt,x0) 1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0,Σq(t) 1−αˉt(1−αt)(1−αˉt−1)I)
通过上面的公式,我们可以知道,当知道 x 0 x_0 x0 和 x t x_t xt, 既可以得到 x t − 1 x_{t-1} xt−1. 但是, 我们没有办法获取真实的 x 0 x_0 x0, 所以只能估计 x t x_t xt 对应的 x ^ 0 \hat{x}_0 x^0 是什么样子的。
μ q ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t Σ q ( t ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I \begin{align} \mu_q(x_t, x_0) &= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}} \\ {\Sigma}_q(t) &= \frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}}\textbf{I} \end{align} μq(xt,x0)Σq(t)=1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0=1−αˉt(1−αt)(1−αˉt−1)I
- 第一种: 先利用预测的噪声 ϵ t \epsilon_t ϵt 估计 x ^ 0 \hat{x}_0 x^0. 然后利用 x t x_t xt 和 x ^ 0 \hat{x}_0 x^0 估计 x t − 1 x_{t-1} xt−1
x ^ 0 t − 1 = x t − 1 − α ˉ t ⋅ ϵ θ ( x t , t ) α ˉ t \begin{align} \hat{x}_0^{t-1} &= \frac{ x_t - \sqrt{1-\bar{\alpha}_t} \cdot \epsilon_{\theta}(x_t, t) }{ \sqrt{\bar{\alpha}_t} } \end{align} x^0t−1=αˉtxt−1−αˉt⋅ϵθ(xt,t)
x ^ 0 t − 1 \hat{x}_0^{t-1} x^0t−1 表示第 t − 1 t-1 t−1时刻估计的 x 0 x_0 x0. 基本上,在采样一半时,基本上预测的 x 0 x_0 x0 就和真实图片差不多了.
接下来计算 x t − 1 x_{t-1} xt−1 的均值和方差. 方差非常重要,不能忽略
m e a n ( x t − 1 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t ⋅ x t + α ˉ t − 1 ( 1 − α t ) 1 − α ˉ t ⋅ x ^ 0 t − 1 v a r ( x t − 1 ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t ⋅ I x t − 1 = m e a n ( x t − 1 ) + v a r ( x t − 1 ) \begin{align} \mathrm{mean}(x_{t-1}) &= \frac{ \sqrt{\alpha_t}(1-\bar{\alpha}_{t-1}) }{ 1-\bar{\alpha}_{t} } \cdot x_t + \frac{ \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t) }{ 1-\bar{\alpha}_{t} } \cdot \hat{x}_0^{t-1} \\ \mathrm{var}(x_{t-1}) &= \frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}} \cdot \textbf{I} \\ x_{t-1} &= \mathrm{mean}(x_{t-1}) + \mathrm{var}(x_{t-1}) \end{align} mean(xt−1)var(xt−1)xt−1=1−αˉtαt(1−αˉt−1)⋅xt+1−αˉtαˉt−1(1−αt)⋅x^0t−1=1−αˉt(1−αt)(1−αˉt−1)⋅I=mean(xt−1)+var(xt−1)
for i, t in enumerate(ddpm_scheduler.timesteps):alpha_t = alphas[t] alpha_t_bar = alphas_cumprod[t]alpha_t_bar_prev = alphas_cumprod[t - 1] if t - 1 >= 0 else torch.tensor(1.0)# -------------## 1. x_0 和 x_t的系数pred_ori_sample_coeff = torch.sqrt(alpha_t_bar_prev) * (1-alpha_t) / (1-alpha_t_bar)current_sample_coeff = torch.sqrt(alpha_t) * (1-alpha_t_bar_prev) / (1-alpha_t_bar)## 2. 预测 x_0noise_pred = ddpm_noise_model(x_t, t)['sample']est_x_0 = (x_t - torch.sqrt(1-alpha_t_bar) * noise_pred) / torch.sqrt(alpha_t_bar)## 3. clip x_0est_x_0 = est_x_0.clamp(-1, 1)## 4. 预测 x_{t-1}x_t_prev = pred_ori_sample_coeff * est_x_0 + current_sample_coeff * x_t## 5. 添加噪声if t > 0:std_var_noise = torch.randn_like(x_t).to(device)x_t_var_coeff = (1-alpha_t) * (1-alpha_t_bar_prev) / (1-alpha_t_bar)x_t_var_coeff = torch.sqrt(x_t_var_coeff)x_t_prev = x_t_prev + x_t_var_coeff * std_var_noisex_t = x_t_prev
相关文章:

diffusion model 学习笔记
条件引导的 diffusion 对于无条件的DDPM 而言 p ( x t ∣ x 0 ) ∼ N ( α t ˉ x 0 , 1 − α t ˉ ⋅ I ) p(x_t | x_0) \sim \mathcal{N}( \sqrt{\bar{\alpha_t}} x_0, 1-\bar{\alpha_t} \cdot \mathrm{I} ) p(xt∣x0)∼N(αtˉ x0,1−αtˉ⋅I) 可以得到…...

【C++题解】1967. 输出字符的ascii码
欢迎关注本专栏《C从零基础到信奥赛入门级(CSP-J)》 问题:1967. 输出字符的ascii码 类型:字符串、字符型 题目描述: 从键盘读入一个字符,请计算并输出该字符的 ascii 码。 比如:字符 ‘A’ …...

Java入门9——类和对象+this+构造方法
终于终于,我们开启了Java的大门!类和对象才是Java梦开始的地方,让我们一起来学习吧! 一、类和对象 通常来讲,一个Java文件里面写一个类,那么类是什么呢? 类,字面意思,就…...

Django目录结构最佳实践
Django项目目录结构 项目目录结构配置文件引用修改创建自定义子应用方法修改自定义注册目录从apps目录开始 项目目录结构 └── backend # 后端项目目录(项目名称)├── __init__.py├── logs # 项目日志目录├── manage.py #…...

npm run dev 报错PS ‘vite‘ 不是内部或外部命令,也不是可运行的程序或批处理文件。
报错场景: 使用npm run dev命令启动项目,报错 PS D:\vuecode\ying-mei> npm run dev > ying-mei0.0.0 dev > vite vite 不是内部或外部命令,也不是可运行的程序 或批处理文件。 原因: 缺失依赖,因为新建的项…...

后端:Spring、Spring Boot-实例化Bean依赖注入(DI)
文章目录 1. 实例化Bean2. 使用FactoryBean3. 依赖注入(DI)3.1 AutoWired 属性注入(查找顺序:先类型,后名字)3.2 AutoWired 在构造函数&参数上的使用3.3 Inject和Resource 进行依赖注入3.4 Value 进行注入 1. 实例化Bean 默认使用无参构造函数&…...

C++ 数据结构 静态顺序表、动态顺序表。
静态顺序表(Static Array List)是一种线性数据结构,通常用数组实现。它具有固定的大小,并在编译时分配内存。以下是静态顺序表的一些基本概念和实现示例。 静态顺序表基本概念 固定大小:静态顺序表的大小在创建时定义…...

QML旋转选择器组件Tumbler
1. 介绍 Tumbler是一个用于创建旋转选择器的组件。它提供了一种直观的方式来让用户从一组选项中进行选择,类似于转盘式数字密码锁。网上找的类似网图如下: 在QML里,这种组件一共有两个版本,分别在QtQuick.Extras 1.4(旧)和QtQuic…...

在工作中常用到的 Linux 命令总结
引言 我之前找工作面试的时候。几乎每次面试几乎都会问到 Linux 常用命令,会问一些命令的应用场景。目的是考察我们是否在实际开发中经常用、用得熟练。今天我就来系统地总结一下开发过程中最常用的 Linux 命令,算是一个复习总结。 基本操作 文件管理…...

反射、枚举和lambda表达式
文章目录 一、反射1.1 什么是反射1.2 反射相关的类1.3 示例获取Class对象通过反射去创建对象调用带两个参数且私有的构造方法获取私有属性反射私有方法 二、枚举2.1 什么是枚举以及其优缺点2.2 如何使用枚举组织常量的基本方法枚举类的其他方法示例枚举能否通过反射拿到实例对象…...

Stable Diffusion Web UI 1.9.4常用插件扩展-WD14-tagger
Stable Diffusion Web UI 1.9.4 运行在 WSL 中的 Docker 容器中 tagger 插件的作用是,上传一张图片,反推这张图片可能的提示词。 使用场景就是,想要得到类似的图片内容时使用。 WD14-tagger 安装 Stable Diffusion WebUI WD14-tagger GitH…...

java 第19天 Lambda、jdk8.0新方法、Optional
一.Lambda表达式 前提是:参数是函数式接口才可以书写Lambda表达式 函数式接口条件: 1.接口 2.只有一个抽象方法 lambda表达式又称为匿名函数,允许匿名函数以参数的形式传入方法,简化代码 lambda表达式分为两部分()->{} …...

江协科技STM32学习- P31 I2C通信协议
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

6、liunx目录的功能
一、目录简介 Linux主要树结构目录包括:/、/root、/home、/usr、/bin、/tmp、/sbin、/proc、/boot 【Linux系统中常见目录功能如下】 / 根目录;/bin 存放必要的命令;(普通用户) /boot 存放内核以及启动所需的文件&…...

挑战Java面试题复习第5天,无人扶我青云志
挑战第 5 天 java反射List Set Map 区别Object 常用方法 java反射 定义: 运行时动态获取类信息和调用方法的特性。 应用场景: JDBC数据库连接。框架如Hibernate和Struts等。 实现方式: 通过四种方法获取Class对象: Class.fo…...

大规模语言模型:从理论到实践(1)
1、绪论 大规模语言模型(Large Language Models,LLM)是由包含数百亿以上参数的深度神经网络构建的语言模型,采用自监督学习方法通过大量无标注文本进行训练。自2018年以来,多个公司和研究机构相继发布了多种模型&#…...

C#如何锁定和解除鼠标及键盘BlockInput
在C#中,"BlockInput"通常指的是一个功能或方法,用于阻止或暂停用户输入一段时间。这在某些特定的应用场景下非常有用,比如在游戏中防止玩家连续快速点击导致游戏逻辑错误,或者在UI应用中防止用户在某个操作正在进行时进…...

Stable Diffusion 3.5发布:图像生成新纪元,多模态AI的突破!
在人工智能的图像生成领域,我们刚刚迎来了一位新的明星——Stable Diffusion 3.5。这是一款由多模态扩散Transformer(MMDiT)驱动的文本到图像模型,它在图像质量、字体处理、复杂提示理解以及资源效率方面都实现了显著提升。今天&a…...

MySQL超大分页怎么优化处理?limit 1000000,10 和 limit 10区别?覆盖索引、面试题
1. limit 100000,10 和 limit 10区别 LIMIT 100000, 10: 这个语句的意思是,从查询结果中跳过前100000条记录,然后返回接下来的10条记录。这通常用于分页查询中,当你需要跳过大量的记录以获取后续的记录时。例如,如果你…...

RabbitMQ 实现消息队列负载均衡
在现代应用程序中,消息队列是一种重要的架构模式,用于解耦服务、处理异步任务和实现负载均衡。其中,RabbitMQ是一个广泛使用的开源消息代理,提供了高可用性、可靠性和灵活性。本文将展示如何使用Python及其pika库来实现RabbitMQ&a…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
