数楼梯(加强版)
数楼梯(加强版)
题目背景:
小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上.
他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题.
题目描述:
1楼到2楼楼梯有n级台阶。小明每次可以爬一格、走两格或者跨三格。问最终有几种方案到二楼?答案对998244353取模。
输入格式:
一行一个数n。
输出格式:
一行一个数,表示方案数。
输入输出样例
输入 #1:
3
输出 #1:
4
输入 #2:
5
输出 #2:
13
提示说明:
n≤1000
时间:1000ms
空间:256M
(上楼梯时不能往回走)
如果觉得这道题太难可以前往P1255先做数楼梯简单版:
https://www.luogu.com.cn/problem/P1255
思路:
1.暴力法
很容易看出来,这是一道递归题,我们可以用暴力递归来解决。
#include<iostream>
using namespace std;
static const int mod=998244353;
long long sum=0;
int n;
long long fun(int x){if(x==n)return 1;if(x>n)return 0;long long s1=0,s2=0,s3=0;s1+=fun(x+1)%mod;s2+=fun(x+2)%mod;s3+=fun(x+3)%mod;return (s1+s2+s3)%mod;
}
int main(){cin>>n;cout<<fun(0)<<endl; return 0;
}但是这个份代码会超时,非常慢,所以要进行优化!
2.递推法
我们用 f(x) 表示爬到第 x 级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
f(x)=f(x−1)+f(x−2)
它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解,因为每次只能爬 1 级或 2 级,所以 f(x) 只能从 f(x−1)和 f(x−2) 转移过来,而这里要统计方案总数,我们就需要对这两项的贡献求和。
以上是动态规划的转移方程,下面我们来讨论边界条件。我们是从第 0 级开始爬的,所以从第 0 级爬到第 0 级我们可以看作只有一种方案,即 f(0)=1;从第 0 级到第 1 级也只有一种方案,即爬一级,f(1)=1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下,根据转移方程得到 f(2)=2,f(3)=3,f(4)=5,……,我们把这些情况都枚举出来,发现计算的结果是正确的。
我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n)的实现,但是由于这里的 f(x) 只和 f(x−1)) 与 f(x−2)有关,所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。下面的代码中给出的就是这种实现。
#include<iostream>
using namespace std;
static const int mod=998244353;
void fun(int n){long long max[1001];int i=0;max[0]=1;max[1]=2;max[2]=4;for(int j=3;j<n;j++)max[j]=(max[j-1]+max[j-2]+max[j-3])%mod;cout<<max[n-1]<<endl;
}
int main(){int n;cin>>n;fun(n); return 0;
}总结:
对于这道题,有些像斐波那契数列,需要将递归进行优化才可以解决。
题目链接:
数楼梯(加强版) - 洛谷https://www.luogu.com.cn/problem/U267577
相关文章:

数楼梯(加强版)
数楼梯(加强版) 题目背景: 小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上. 他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题. 题目描述: 1楼到2楼楼梯有n级台阶。小明每…...

MySQL-数据类型
数据类型简介数据表由多列字段构成,每一个字段指定了不同的数据类型,指定了数据类型之后,也就决定了向字段插入的数据内容。不同的数据类型也决定了 MySQL 在存储它们的时候使用的方式,以及在使用它们的时候选择什么运算符号进行运…...

剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)
剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)1. 题目2. 解题思路3. 数据类型功能函数总结4. java代码5. 踩坑记录1. 题目 从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。 例如: 给定二叉…...

C#网络爬虫开发
1前言爬虫一般都是用Python来写,生态丰富,动态语言开发速度快,调试也很方便但是我要说但是,动态语言也有其局限性,笔者作为老爬虫带师,几乎各种语言都搞过,现在这个任务并不复杂,用我…...

Fastjson 总结
0x00 前言 这一篇主要是针对已经完成的fastjson系列做一个知识点总结,一来是为了更加有条理的梳理已经存在的内容,二来是为了更好的复习和利用。 0x01 Fastjson基础知识点 1.常见问题: 问:fastjson的触发点是什么?…...

文件路径模块os.path
文件路径模块os.path 文章目录文件路径模块os.path1.概述2.解析路径2.1.拆分路径和文件名split2.2.获取文件名称basename2.3.返回路径第一部分dirname2.4.扩展名称解析路径splitext2.5.返回公共前缀路径commonprefix3.创建路径3.1.拼接路径join3.2.获取家目录3.3.规范化路径nor…...
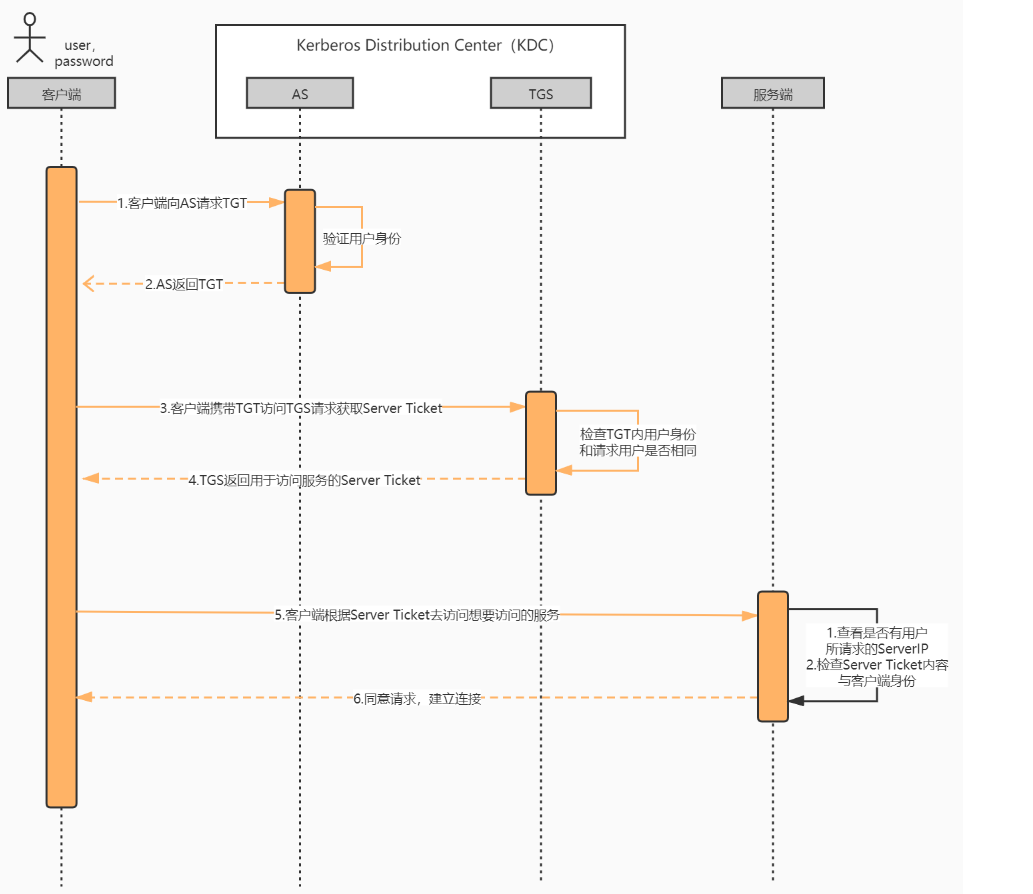
Kerberos简单介绍及使用
Kerberos作用 简单来说安全相关一般涉及以下方面:用户认证(Kerberos的作用)、用户授权、用户管理.。而Kerberos功能是用户认证,通俗来说解决了证明A是A 的问题。 认证过程(时序图) 核心角色/概念 KDC&…...

DOM编程-全选、全不选和反选
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>全选、全不选和反选</title> </head> <body bgcolor"antiquewhite"> <script type"text/jav…...

C++11可变模板参数
C11可变模板参数一、简介二、语法三、可变模版参数函数3.1、递归函数方式展开参数包3.2、逗号表达式展开参数包一、简介 C11的新特性–可变模版参数(variadic templates)是C11新增的最强大的特性之一,它对参数进行了高度泛化,它能…...

Linux多线程
目录 一、认识线程 1.1 线程概念 1.2 页表 1.3 线程的优缺点 1.3.1 优点 1.3.2 缺点 1.4 线程异常 二、进程 VS 线程 三、Linux线程控制 3.1 POSIX线程库 3.1 线程创建 3.3 线程等待 3.4 线程终止 3.4.1 return退出 3.4.2 pthread_exit() 3.4.3 pthread_cancel…...
Webpack5 环境下 Openlayers 标注(Icon) require 引入图片问题
Webpack5 环境下 Openlayers 标注(Icon) require 引入图片问题环境版本Openlayers 使用 require 问题Webpack5 正确配置构建新环境的时候,偶然发现 Openlayers 使用 require 的方式加载图片(Icon)报错,开始…...

Zookeeper安装部署
文章目录Zookeeper安装部署Zookeeper安装部署 将Zookeeper安装包解压缩, [rootlocalhost opt]# ll 总用量 14032 -rw-r--r--. 1 root root 12392394 10月 13 11:44 apache-zookeeper-3.6.0-bin.tar.gz drwxrwxr-x. 6 root root 4096 10月 18 01:44 redis-5.0.4 …...
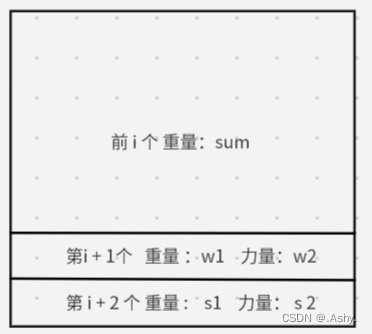
Cow Acrobats ( 临项交换贪心 )
题目大意: N 头牛 , 每头牛有一个重量(Weight)和一个力量(Strenth) , N头牛进行排列 , 第 i 头牛的风险值为其上所有牛总重减去自身力量 , 问如何排列可以使最大风险值最小 , 求出这个最小的最大风险值&am…...

MySQL:为什么说应该优先选择普通索引,尽量避免使用唯一索引
前言 在使用MySQL的过程中,随着表数据的逐渐增多,为了更快的查询我们需要的数据,我们会在表中建立不同类型的索引。 今天我们来聊一聊,普通索引和唯一索引的使用场景, 以及为什么说推荐大家优先使用普通索引…...

Spring Cloud alibaba之Feign
JAVA项目中如何实现接口调用?HttpclientHttpclient是Apache Jakarta Common下的子项目,用来提供高效的、最新的、功能丰富的支持Http协议的客户端编程工具包,并且它支持HTTP协议最新版本和建议。HttpClient相比传统JDK自带的URL Connection&a…...
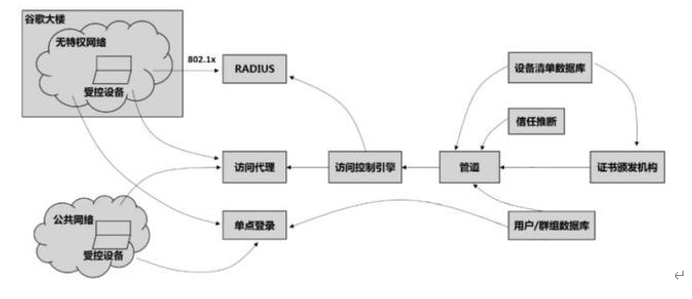
零信任-Google谷歌零信任介绍(3)
谷歌零信任的介绍? "Zero Trust" 是一种网络安全模型,旨在通过降低网络中的信任级别来防止安全威胁。在零信任模型中,不论请求来自内部网络还是外部网络,系统都将对所有请求进行详细的验证和审核。这意味着每次请求都需…...
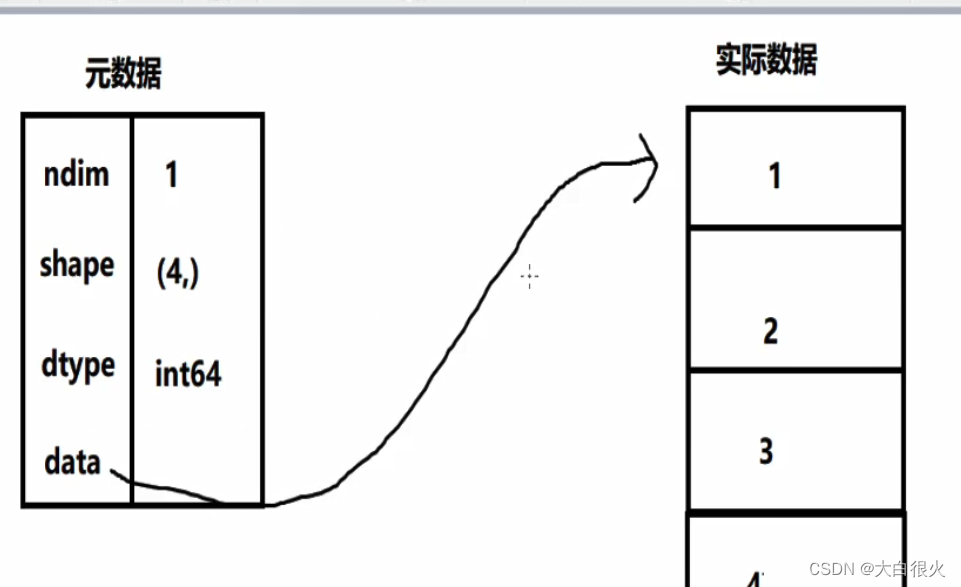
Numpy基础——人工智能基础
文章目录一、Numpy概述1.优势2.numpy历史3.Numpy的核心:多维数组4.numpy基础4.1 ndarray数组4.2 内存中的ndarray对象一、Numpy概述 1.优势 Numpy(Nummerical Python),补充了Python语言所欠缺的数值计算能力;Numpy是其它数据分析及机器学习库的底层库&…...

电商仓储与配送云仓是什么?
仓库是整个供给链的关键局部。它们是产品暂停和触摸的点,耗费空间和时间(工时)。空间和时间反过来也是费用。经过开发数学和计算机模型来微调仓库的规划和操作,经理能够显著降低与产品分销相关的劳动力本钱,进步仓库空间应用率,并…...

【零基础入门前端系列】—HTML介绍(一)
【零基础入门前端系列】—HTML介绍(一) 一、什么是HTML HTML是用来描述网页的一种语言HTML指的是超文本标记语言:HyperText Markup LanguageHTML不是一种编程语言,而是一种超文本标记语言,标记语言是一套标记标签(ma…...

Elasticsearch索引库和文档的相关操作
前言:最近一直在复习Elasticsearch相关的知识,公司搜索相关的技术用到了这个,用公司电脑配了环境,借鉴网上的课程进行了总结。希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么需要…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
