当前位置：首页 > news >正文

信号与噪声分析——第二节：随机变量的统计特征

news 2026/2/9 23:08:51

2.1 单个随机变量的统计特征

随机变量是什么？

当随机变量X的取值个数是有限个的时候，我们称它为离散随机变量。

当随机变量X的取值个数是无限个的时候，我们称它为连续随机变量。

1. 分布函数和概率密度

1.分布函数

分布函数 $F(x)$ 定义为随机变量 $X$ 小于或等于某个值 $x$ 的概率，即：
$F(x) = P(X \leq x)$ $-\infty <x<\infty$

这表示随机变量在 $x$ 及其以下取值的累积概率。

分布函数具有以下性质：

单调非减性：对于任意 $x_1 < x_2$ ，有 $F(x_1) \leq F(x_2)$

即： $F(x_2)-F(x_1)= P\left \{x_1< X \leqslant x_2 \right \}\geqslant 0$

且： $P\left \{ x_1< X\leq x_2 \right \}=P\left \{ X\leq x_2 \right \}-P\left \{ X\leq x_1 \right \}=F(x_2)-F(x_1)$

极限性质：当 $x \to -\infty$ ， $F(x) \to 0$ ；当 $x \to +\infty$ ， $F(x) \to 1$

2. 概率密度函数

        对于连续型随机变量，概率密度函数 $p(x)$ 是分布函数的导数，即：
                                                 $p(x) = \frac{dF(x)}{dx}$
        概率密度函数通常用于描述连续型变量，表示在某个特定点附近随机变量取值的密度，而不是直接的概率值。

总的来说就是：概率密度函数并不直接表示某个点取值的概率，而是用来计算区间上的概率

比如区间对于 $[a,b]$ ，有：
$P(a<X \leq b) = \int_a^b p(x) dx$

概率密度函数的性质：

1. 非负性
                对于任意的 $x$ ，概率密度函数 $p(x)\geqslant 0$
                                         $p(x) \geq 0, \quad \forall x \in \mathbb{R}$

2. 积分为1
                整个实数范围内的概率密度函数积分等于1

                                         $\int_{-\infty}^{+\infty} p(x) dx = 1$

3. 在任意区间上的概率
        概率密度函数并不直接表示某个点取值的概率，而是用来计算区间上的概率                                       $P(a<X \leq b) = \int_a^b p(x) dx$

4. 概率密度函数等于分布函数对x求导：

                                                 $p(x) = \frac{dF(x)}{dx}$

2. 随机变量的数字特征

随机变量的数字特征是用来描述随机变量行为的统计量，主要包括数学期望、方差、协方差和相关系数

1. 数学期望（均值）

数学期望是随机变量取值的加权平均，反映了随机变量的中心位置
对于连续型随机变量，其期望为：
$E(X) = \int_{-\infty}^{+\infty} x p(x) \, dx$ (其中 $p(x)$ 为随机变量的概率密度)

2. 方差

方差衡量随机变量取值的波动性，定义为期望与其均值的偏差平方的期望：
$D(X) = E[X - E(X)]^{2}= E(X^2) - E^{2}(X)=\sigma ^{2}_x$

2.2 多个随机变量的统计特征

二维随机变量是两个随机变量 $(X, Y)$ 组成的随机变量向量。

连续型二维随机变量
如果 $X$ 和 $Y$ 是连续型随机变量，它们的联合概率密度函数 $p_{X,Y}(x, y)$ 定义为：
$P(a \leq X \leq b, c \leq Y \leq d) = \int_{a}^{b} \int_{c}^{d} p_{X,Y}(x, y) \, dx\, dy$
该联合密度函数给出了 $X$ 和 $Y$ 同时落在某些区间内的概率。

1. 二维随机变量的分布函数和概率密度函数：

1.联合分布函数：

对于两个随机变量 $X$ 和 $Y$ ，其联合分布函数定义为：
$F(x, y) = P(X \leq x, Y \leq y)$
这个函数表示随机变量 $X$ 和 $Y$ 同时小于或等于某个值的概率。

如果：

$F(x,y)=F(x)F(y)$

则称X和Y相互独立。

2. 联合概率密度函数：

对于连续型随机变量，联合概率密度函数 $p(x,y)$ 定义为：
$p(x, y) = \frac{\partial^2 F(x, y)}{\partial x \partial y}$

联合概率密度的归一性：

$\iint_{-\infty}^{+\infty} p(x, y) \, dx \, dy = 1$

如果：

$p(x,y)=p(x)p(y)$

则称X和Y相互独立。

$p(x,y)=p(x)p(y)$ , $F(x,y)=F(x)F(y)$ 是X和Y相互独立的充要条件

3. 边缘分布

        边缘分布是从联合分布中提取单个随机变量的分布。对于联合概率密度函数，可以通过对其他变量积分得到边缘概率密度：
                                         $p_X(x) = \int_{-\infty}^{+\infty} p(x, y) \, dy$
                                         $p_Y(y) = \int_{-\infty}^{+\infty} p(x, y) \, dx$

2. 二维随机变量的数字特征：

二维随机变量的数字特征是用于定量描述两个随机变量之间的特性以及它们之间相互关系的统计量。

1. 联合期望

连续型随机变量：

                                         $E(X+Y)=E(X)+E(Y)$
                         $E(X) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x p_{X,Y}(x, y) \, dx \, dy$
                         $E(Y) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} y p_{X,Y}(x, y) \, dx \, dy$
其中， $p_{X,Y}(x, y)$ 是 $X$ 和 $Y$ 的联合概率密度函数

如果：随机变量X和Y相互独立，且 $E(X)$ 和 $E(Y)$ 存在，则 $E(XY)$ 也存在，则有

                                                 $E(XY)=E(X)E(Y)$

2. 联合方差

对于 $X$ 的方差：
                 $D(X) = E[X - E(X)]^{2} = E(X^2) - E^{2}(X)$

对于 $Y$ 的方差：
                 $D(Y) = E[Y - E(Y)]^{2} = E(Y^2) - E^{2}(Y)$

对于连续型随机变量的联合方差：
                         $E(X^2) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x^2 p_{X,Y}(x, y) \, dx \, dy$

3. 协方差

协方差用于衡量两个随机变量之间的线性相关性。它反映了两个变量是如何一起变化的：当一个变量增加时，另一个变量是否也有增加（正相关）或减少（负相关）的趋势。

对于两个随机变量 $X$ 和 $Y$ ，它们的协方差定义为：

$\text{Cov}(X, Y) = E[(X - E(X))(Y - E(Y))] =R(X,Y)-m_xm_y$

$\text{Cov}(X, Y) = E(XY) - E(X)E(Y)$

4. 归一化协方差函数——相关系数

        相关系数是协方差的标准化形式，用于定量衡量两个随机变量之间的线性相关性。相关系数的取值范围为 $[-1, 1]$ ：

                                                $\rho_{X,Y} = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y}$

其中 $\sigma_X$ 和 $\sigma_Y$ 分别是 $X$ 和 $Y$ 的标准差，定义为：
                                         $\sigma_X = \sqrt{D(X)}, \quad \sigma_Y = \sqrt{D(Y)}$

5. 相关函数：

$R(X,Y)=E[XY]= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xy p_{X,Y}(x, y) \, dx \, dy$

信号与噪声分析——第二节：随机变量的统计特征

2.1 单个随机变量的统计特征随机变量是什么？ 当随机变量X的取值个数是有限个的时候，我们称它为离散随机变量。当随机变量X的取值个数是无限个的时候，我们称它为连续随机变量。 1. 分布函数和概率密度 1.分布函数分布函数定义为随机变…...

编程日记 2024/11/6 9:04:55

PHP网络爬虫常见的反爬策略

PHP网络爬虫在抓取数据时，常常会遭遇各种反爬策略。这些策略是网站为了保护自身数据不被恶意爬取而设置的。以下是一些常见的PHP网络爬虫反爬策略： IP限制： 这是最常见的反爬虫技术。通过限制IP的访问，可以有效防止恶意的爬虫攻击…...

编程日记 2024/11/6 9:03:54

java java.util.Scanner设置编码

在Java中，可以通过设置Scanner对象的编码来读取特定编码的输入。使用Scanner的构造方法时，可以传入一个InputStream对象作为参数来设置编码。例如，如果要设置编码为UTF-8，可以这样写： InputStream inputStream Syst…...

编程日记 2024/11/6 9:02:53

小菜家教平台（二）：基于SpringBoot+Vue打造一站式学习管理系统

目录前言今日进度详细过程一、数据库重构二、编写登录接口相关知识点前言昨天我们重启了小菜家教平台的开发，创建了新项目并初步进行了配置，今天我们继续。大家要是有需要源码的话可以在评论区跟我说，博客中就不添加源码了~ 今…...

编程日记 2024/11/6 9:00:50

Android AndroidManifest 文件内标签及属性

以下是重新排版后的文章： AndroidManifest 1. <manifest> 它是AndroidManifest.xml文件的根标签，包含了整个应用程序的基本信息，如应用程序的包名、版本代码、版本名称等。所有其他标签几乎都是在manifest标签内部定义的。示例&…...

编程日记 2024/11/6 8:57:47

修改sql server 数据库的排序规则Chinese_PRC_CI_AS（字符集+排序）

文章目录引言I 解决方案案例II 知识扩展排序规则SQL SERVER支持的所有排序规则引言新增sql server 数据库实例的默认排序规则不支持中文存储，导致乱码解决方案：修改排序规则为Chinese_PRC_CI_AS 或者 Chinese_PRC_Stroke_CI_AS_WS或者Chinese_PRC_CI_AI_KS_WS 仅对新增…...

编程日记 2024/11/6 8:55:45

【ChatGPT】让ChatGPT在回答中附带参考文献与来源

让ChatGPT在回答中附带参考文献与来源在撰写内容时，引用参考文献和来源可以增强信息的可信度和权威性。通过引导ChatGPT生成带有参考文献的回答，用户能够获取更可靠的信息和背景资料。本文将探讨如何有效地引导ChatGPT在回答中附带参考文献与来源。一…...

编程日记 2024/11/6 8:50:40

大屏可视化：舞动数据与美观的“设计秘籍”

大屏可视化鉴赏：踏入软件系统产品设计之旅，让我们一同鉴赏那些闪耀在智慧农业、智慧园区、智慧社区及智慧港口等领域的大屏可视化杰作。每一帧画面，都是科技与创新的完美融合，数据跃然屏上，智慧触手可及。 >> 数…...

编程日记 2024/11/6 8:44:33

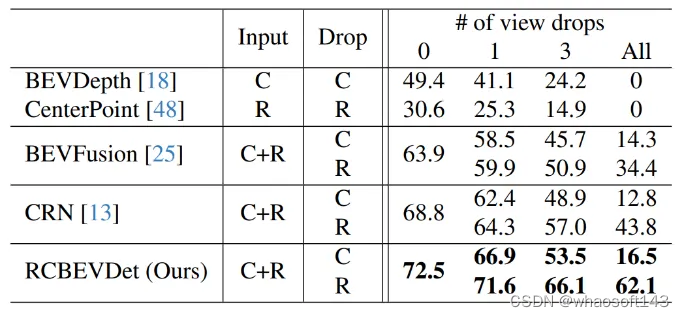
w~视觉~3D~合集1

我自己的原文哦~ https://blog.51cto.com/whaosoft/12316553 #SAFDNet 3D点云物体检测对自动驾驶感知至关重要，如何高效地从稀疏点云数据中学习特征表示是3D点云物体检测面临的一个关键挑战。我们在本文中将会介绍团队发表在NeurIPS 2023的HEDNet和CVPR 2024的SAFD…...

编程日记 2024/11/6 8:42:28

android 怎么查看依赖包的大小

Android 项目依赖包大小查看方案在 Android 项目开发过程中，依赖包管理是一个非常重要的环节。了解每个依赖包的大小有助于我们优化应用性能，减少应用安装包的大小。本文将介绍一种方法来查看 Android 项目中各个依赖包的大小。 1. 环境准备在开始之…...

编程日记 2024/11/6 8:39:23

HyperLogLog 的原理详解

HyperLogLog（简称 HLL）是一种用于近似计数（特别是基数估计，Cardinality Estimation）的算法，它能够在大数据场景中高效地估计集合中不同元素的数量，尤其适用于数据流的情况。HyperLogLog 相较于传…...

编程日记 2024/11/6 8:37:21

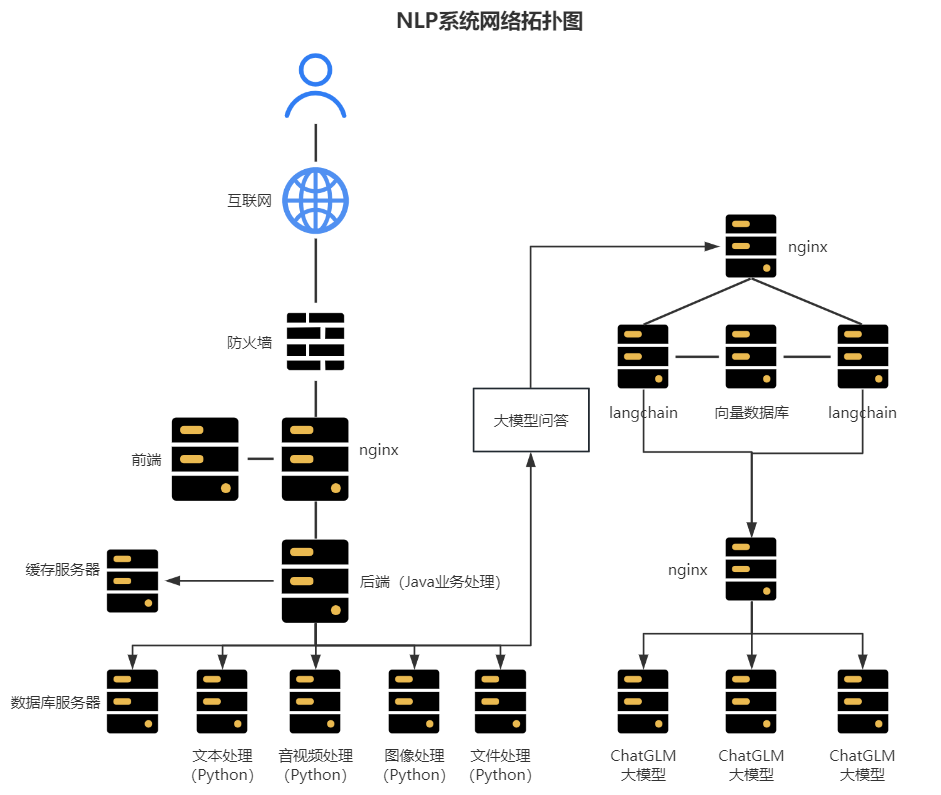
OCR、语音识别与信息抽取：免费开源的AI平台在医疗领域的创新应用

一、系统概述在医疗行业中，大量数据来自手写病历、医学影像报告、患者对话记录等非结构化数据源。这些数据常常存在信息碎片化和管理困难的问题，给医务人员的工作带来了不便。思通数科AI多模态能力平台正是为了解决这一行业痛点而生，产品集…...

编程日记 2024/11/6 8:36:19

苍穹外卖Bug集合

初始化后端项目运行出现以下问题以上报错是因为maven和jdk版本不符合，需要将jdk改成17，mavne改成3.9.9...

编程日记 2024/11/6 8:35:17

小菜家教平台（一）：基于SpringBoot+Vue打造一站式学习管理系统

前言现在已经学习了很多与Java相关的知识，但是迟迟没有进行一个完整的实践（之前这个项目开发到一半，很多东西没学搁置了，同时原先的项目中也有很多的问题），所以现在准备从零开始做一个基于SpringBootVue的…...

编程日记 2024/11/6 8:33:15

PyCharm中pylint安装与使用

目录 1. 安装插件2. pycharm中使用该功能3. 命令行使用 1. 安装插件然后重启 2. pycharm中使用该功能 3. 命令行使用前提是先 pip install pylint pylint demo01.py下面红框内容的意思是，得到10分/ 满分10分，上次运行获得8.33分，经调整…...

编程日记 2024/11/6 8:31:11

一篇文章了解TCP/IP模型

TCP/IP模型，即传输控制协议/互联网协议模型（Transmission Control Protocol/Internet Protocol Model），是互联网及许多其他网络上使用的分层通信模型。以下是对TCP/IP模型的详细介绍： 一、定义与组成TCP/IP模型是一个四…...

编程日记 2024/11/6 8:28:08

百度智能云账户注册：https://console.bce.baidu.com/ai/#/ai/ocr/app/list 获取appid、api_key、secret_key from aip import AipOcr import osconfig {appid: 116122887,api_key: DAQnt...,secret_key: 5S0Kpyh.... }# 初始化 AipOcr 客户端 client AipOcr(c…...

编程日记 2024/11/6 8:26:07

linux下linuxdeployqt打包过程

一、linuxdeployqt下载安装 1.下载linuxdeployqt依赖拷贝工具下载地址：https://github.com/probonopd/linuxdeployqt/releases 2.为了方便使用，将名字改短一点：mv linuxdeployqt-6-x86_64.AppImage linuxdeployqt3.修改下载的文件的可执行…...

编程日记 2024/11/6 8:25:05

【拥抱AI】AI大模型在软件开发中的应用如何保证数据安全？

随着AI大模型在软件开发中的广泛应用，数据安全问题变得尤为重要。确保数据的安全不仅关乎企业的声誉和合规性，还直接影响到用户对产品的信任。以下是几种常见的方法和最佳实践，以确保在使用AI大模型时的数据安全。 1. 数据加密传输加密&a…...

编程日记 2024/11/6 8:24:04

华为云AI开发平台ModelArts

华为云ModelArts：重塑AI开发流程的“智能引擎”与“创新加速器”！ 在人工智能浪潮席卷全球的2025年，企业拥抱AI的意愿空前高涨，但技术门槛高、流程复杂、资源投入巨大的现实，却让许多创新构想止步于实验室。数据科学家…...

编程新知 2026/2/8 4:37:19

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向深度学习与微纳光子学的结合主要集中在以下几个方向： 逆向设计通过神经网络快速预测微纳结构的光学响应，替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。特征提取与优化从复杂的光学数据中自…...

编程新知 2026/2/8 15:03:04

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留，CCA-Attention为LLM长文本建模带来突破性进展琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制（CCA-Attention），…...

编程新知 2026/2/5 4:25:15

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例

使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件，常用于在两个集合之间进行数据转移，如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。核心特性与用法基本属性 v-model：绑定右侧列表的值&…...

编程新知 2026/2/4 4:25:40

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括：采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中，设置任务排序规则尤其重要，因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

Java - Mysql数据类型对应

Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

编程新知 2025/12/14 11:45:25

Docker 本地安装 mysql 数据库

Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ；并安装。基础操作不再赘述。打开 macOS 终端，开始 docker 安装mysql之旅第一步 docker search mysql 》〉docker search mysql NAME DE…...

编程新知 2026/2/9 17:06:25