54. 螺旋矩阵
https://leetcode.cn/problems/spiral-matrix/description/?envType=study-plan-v2&envId=top-100-liked
观察示例中的输出轨迹我们可以想到如下设计: 1.在朝某一方向行进到头后的改变方向是确定的,左->下,下->右,右->上,上->左 2.在各个方向的边界也是可以确认的,在改变方向后,行进方向上的边界需要改变,向右上边界+1,向下右边界-1,向左下边界 3.可以通过边界和计数来判度是否结束 初始边界:上:0,右:matrix[0].length-1,下:matrix.length-1,左:0
public static void main(String[] args) {int[][] matrix = {{1,2,3},{4,5,6},{7,8,9}};System.out.println(new Solution().spiralOrder(matrix));}public List<Integer> spiralOrder(int[][] matrix) {// 定义左、上、右、下边界int lBoundary = 0, upBoundary = 0, rBoundary = matrix[0].length - 1, dBoundary = matrix.length - 1;// 定义方向,0:向右,1:向下,2:向左,3:向上int direction = 0;// 计数int count = 0;// 总数int sum = matrix.length * matrix[0].length;// 结果列表List<Integer> res = new ArrayList<>();// 当计数小于总数时,继续循环while(count < sum){// 向右if(direction == 0){// 从左边界到右边界,依次添加元素for(int i = lBoundary; i <= rBoundary; i++){res.add(matrix[upBoundary][i]);count++;}// 上边界下移upBoundary++;}// 向下if(direction == 1){// 从上边界到下边界,依次添加元素for(int i = upBoundary; i <= dBoundary; i++){res.add(matrix[i][rBoundary]);count++;}// 右边界左移rBoundary--;}// 向左if(direction == 2){// 从右边界到左边界,依次添加元素for(int i = rBoundary; i >= lBoundary; i--){res.add(matrix[dBoundary][i]);count++;}// 下边界上移dBoundary--;}// 向上if(direction == 3){// 从下边界到上边界,依次添加元素for(int i = dBoundary; i >= upBoundary; i--){res.add(matrix[i][lBoundary]);count++;}// 左边界右移lBoundary++;}// 改变方向direction = (direction + 1) % 4;}return res;}相关文章:

54. 螺旋矩阵
https://leetcode.cn/problems/spiral-matrix/description/?envTypestudy-plan-v2&envIdtop-100-liked观察示例中的输出轨迹我们可以想到如下设计: 1.在朝某一方向行进到头后的改变方向是确定的,左->下,下->右,右->…...

剧本杀小程序,市场发展下的新机遇
剧本杀作为休闲娱乐的一种游戏方式,在短时间内进入了大众视野中,受到了广泛关注。近几年,剧本杀行业面临着创新挑战,商家需求寻求新的发展机遇,在市场饱和度下降的趋势下,获得市场份额。 随着科技的不断进…...

【系统架构设计师】论文:论基于 ABSD 的软件开发
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 摘要正文摘要 2022年5月,我就职的公司承接了xx的智慧党建工作,建设“党建红云” 系统,为xx公司的党组织提供觉务管理、服务功能,促进党员学习和党组织交流。我在该项目中承担架构设计师的职责,主导需求分析和…...

为什么OLED透明屏在同类产品中显示效果最好
说起OLED透明屏,这家伙在同类产品里那真的是“一枝独秀”啊!为啥这么说呢?且听我细细道来。 首先,OLED透明屏的透明度那是杠杠的!它不像传统显示屏那样有个固定的背景,而是可以实现像素级的透明效果。这样一…...

深度学习基础知识-Batch Normalization(BN)超详细解析
一、背景和问题定义 在深层神经网络(Deep Neural Networks, DNNs)中,层与层之间的输入分布会随着参数更新不断发生变化,这种现象被称为内部协变量偏移(Internal Covariate Shift)。具体来说,由…...

基于单片机的燃气报警阀门系统
本设计基于单片机的燃气报警阀门系统,燃气报警阀门系统采用STM32主控制器为核心芯片,外围电路由燃气传感器、OLED液晶显示模块、按键模块、蜂鸣器报警模块、电磁阀以及SIM800模块等模块组成。燃气传感器模块负责采集燃气浓度数据,采集完成由S…...

watch与computed的区别、运用的场景
computed和watch都是响应式数据变化的重要机制,但它们在功能、使用场景和性能表现上有显著的区别。 主要区别 功能和用途 1、computed:计算属性,用于基于其他数据属性进行计算,并返回一个结果。它具有缓存机制,只有当…...
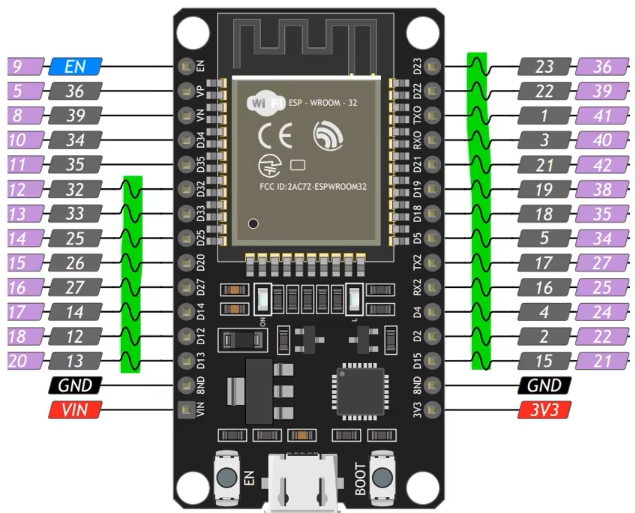
【ESP32+MicroPython】开发环境部署
本教程将指导你如何在Visual Studio Code(VSCode)中设置ESP32的MicroPython开发环境。我们将涵盖从安装Python到烧录MicroPython固件的整个过程,以及如何配置VSCode以便与ESP32进行交互。 准备工作 安装Python 确保你的计算机上安装了Pyth…...

Vision - 开源视觉分割算法框架 Grounded SAM2 配置与推理 教程 (1)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/143388189 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 Ground…...

DAY21|二叉树Part08|LeetCode: 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录 LeetCode: 669. 修剪二叉搜索树 基本思路 C代码 LeetCode: 108.将有序数组转换为二叉搜索树 基本思路 C代码 LeetCode: 538.把二叉搜索树转换为累加树 基本思路 C代码 LeetCode: 669. 修剪二叉搜索树 力扣代码链接 文字讲解:LeetCode: 669. 修剪二叉搜…...

在gitlab,把新分支替换成master分支
1、备份master分支,可以打tag 2、删除master分支 正常情况下,master分支不允许删除,需要做两个操作才能删除 a、变更项目默认分支为非master分支,可以先随便选择 b、取消master为非保护分支 操作了上述两步,就可以删…...

使用 Spring Boot 集成 Thymeleaf 和 Flying Saucer 实现 PDF 导出
在 Spring Boot 项目中,生成 PDF 报表或发票是常见需求。本文将介绍如何使用 Spring Boot 集成 Thymeleaf 模板引擎和 Flying Saucer 实现 PDF 导出,并提供详细的代码实现和常见问题解决方案。 目录 一、项目依赖二、创建 Thymeleaf 模板三、创建 PDF 生…...

web——upload1——攻防世界
第一次做木马题目,有点懵逼,浮现一下做题思路 可以上传一个文件,通过学习学习到了一句话木马 一句话木马: 利用文件上传漏洞,往目标网站中上传一句话木马,然后你就可以在本地通过中国菜刀chopper.exe即可…...

nginx 搭建网站
1.查看防火墙状态systemctl status firewalld 2.getenforce 3.安装nginx yum install nginx -y 4.网站信息 echo "welcome to yinchuankejixuanyuan" > /usr/share/nginx/html/index.html 5.查看命令状态 nginx -t 6.重启 systemctl restart nginx...

Java基础-Java中的常用类(上)
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 String类 创建字符串 字符串长度 连接字符串 创建格式化字符串 String 方法 System类 常用方法 方…...

气压仪器智能打气泵方案芯片SIC8833
智能打气泵方案最开始是机械式的开发,后来慢慢地演变成由一个气缸、压力传感器和主控芯片的开发的PCBA方案,它具备小体积、智能数显、预设胎压、动态测量、精准压力检测以及过充过放等功能。 其方案设计原理是利用主控芯片和压力传感器的组合设计&#x…...
的定位和专业:完善产品;专业;非助手;自动化)
软件测试(系统测试)的定位和专业:完善产品;专业;非助手;自动化
软件测试(系统测试)的定位 在研发流程的后端,测试并非无中生有的创举,而是从既有基础(即“1”)出发,致力于推动产品向更高层次(即从“1”到“100”)的跃升与完善。在这一…...

2024 CSS保姆级教程四
CSS中的动画 CSS动画(CSS Animations)是为层叠样式表建议的允许可扩展标记语言(XML)元素使用CSS的动画的模块 即指元素从一种样式逐渐过渡为另一种样式的过程 常见的动画效果有很多,如平移、旋转、缩放等等&#…...

PostgreSQL技术内幕17:PG分区表
文章目录 0.简介1.概念介绍2.分区表技术产生的背景3.分区类型及使用方式4.实现原理4.1 分区表创建4.2 分区表查询4.3 分区表写入4.4 分区表删除 0.简介 本文主要介绍PG中分区表的概念,产生分区表技术的原因,使用方式和其内部实现原理,旨在能…...

群控系统服务端开发模式-应用开发-上传工厂开发
现在的文件、图片等上传基本都在使用oss存储。而现在常用的oss存储有阿里云、腾讯云、七牛云、华为云等,但是用的最多的还是前三种。而我主要封装的是本地存储、阿里云存储、腾讯云存储、七牛云存储。废话不多说,直接上传设计图及说明,就一目…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
