代码随想录第二十二天
回溯算法理论介绍
回溯算法是一种基于递归思想的算法设计技术,适用于解决需要构造所有解或找到特定解的组合问题。回溯的基本思路是通过系统地搜索所有可能的解决方案,然后逐步撤销不符合要求的选择,回到上一步继续尝试。这种算法最适合应用于决策树、排列组合、子集生成等涉及多阶段决策问题的场景。
如何理解回溯算法
回溯法解决的问题都可以抽象为树形结构,是的,我指的是所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
回溯算法的一般结构
void backtrack(参数) {if (满足结束条件) {记录解或返回;}for (选择 in 可选择列表) {做出选择;backtrack(新的参数); // 递归调用继续做下一步选择撤销选择; // 撤销选择,回到上一步的状态}
}
剪枝套路
剪枝(Pruning)是一种优化回溯算法的技术,用于在搜索过程中减小问题规模、提高效率,从而避免不必要的计算。它的核心思想是:在构造解决方案的过程中,如果发现某些部分已经不能通向一个可行的解,就可以提前结束这条路径的搜索,直接“剪掉”这部分的搜索空间,从而节省时间。
简单来说,剪枝就是在回溯过程中“提前发现死胡同”,然后立刻停止当前的搜索,而不是继续探索下去。这样可以减少不必要的计算量,极大地提高回溯的效率。
77.组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
思路:
最开始的思路就是按照回溯算法的模板写的,这道题的目的是从范围 [1, n] 中选取 k 个数,生成所有可能的组合,并返回这些组合。解决这道题的有效方法是使用回溯算法。回溯的基本思路是逐步尝试所有可能的选择,并通过递归进行深度优先搜索。在每次递归过程中,我们依次选择一个新的数字加入当前组合,如果当前组合的大小达到了 k,就将其存储为一个有效解。在这之后,我们会通过回溯(撤销选择的方式返回到上一步,尝试其他可能的选择,从而确保找到所有的组合解。为了优化算法,我们应用了剪枝策略,即在递归过程中,如果剩余的可选数字数量不足以组成完整的组合,我们会提前终止当前路径,从而减少不必要的计算,提高效率。通过这种逐步尝试、回退、剪枝的过程,最终生成并返回所有符合要求的组合。
解答:
第一次尝试(超出内存范围)
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
void travelback(int n,int k,int start,int* num,int combinesize,int*** result,int* returnSize,int** returnColumnSizes)
{if(combinesize == k){(*returnSize)++;*result = realloc(*result,(*returnSize)*sizeof(int*));(*result)[(*returnSize)-1] = malloc(sizeof(int)*k);for(int i = 0;i < k;i++){(*result)[(*returnSize)-1][i] = num[i];}*returnColumnSizes = realloc(*returnColumnSizes,(*returnSize)*sizeof(int));(*returnColumnSizes)[(*returnSize)-1] = k;return;}for(int i = start;i <= n;i++){num[combinesize] = i;travelback(n,k,i+1,num,combinesize+1,result,returnSize,returnColumnSizes);}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {*returnSize = 0;*returnColumnSizes = NULL;int** result = NULL;int* num = malloc(sizeof(int)*k);travelback(n,k,1,num,0,&result,returnSize,returnColumnSizes);return result;
}
最终答案(gpt帮助)
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
long long factorial(int n) {long long result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}
int combinationCount(int n, int k) {return factorial(n) / (factorial(k) * factorial(n - k));
}
void travelback(int n, int k, int start, int* num, int combinesize, int** result, int* returnSize) {if (combinesize == k) {for (int i = 0; i < k; i++) {result[*returnSize][i] = num[i];}(*returnSize)++;return;}for (int i = start; i <= n; i++) {num[combinesize] = i;travelback(n, k, i + 1, num, combinesize + 1, result, returnSize);}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {*returnSize = 0;int totalCombinations = combinationCount(n, k);int** result = malloc(totalCombinations * sizeof(int*));for (int i = 0; i < totalCombinations; i++) {result[i] = malloc(k * sizeof(int));}*returnColumnSizes = malloc(totalCombinations * sizeof(int));for (int i = 0; i < totalCombinations; i++) {(*returnColumnSizes)[i] = k;}int* num = malloc(k * sizeof(int));travelback(n, k, 1, num, 0, result, returnSize);free(num);return result;
}
216.组合总和 |||
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
提示:
2 <= k <= 91 <= n <= 60
思路:
这道题与上面很像,但是这道题多了一点条件,所以我们在终止条件下要分成两个部分,当它找的元素已经有要求的那么多个的时候,我们对其进行检测,如果最终结果等于它所要求的结果,那么这是我们需要取得一个数组,如果不是直接返回出去,而我们在取值上面也有变化,我们有一个变量叫做sum是用来进行计算总和的,我们先把这个数值加上,如果不满足的话我们又重新剪掉,最终返回答案。
解答:
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
void travelback(int k,int n,int start,int* num,int combinesize,int*** result,int* returnSize,int** returnColumnSizes,int sum)
{if(combinesize == k){if(sum == n){(*returnSize)++;*result = realloc(*result,(*returnSize)*sizeof(int*));(*result)[(*returnSize)-1] = malloc(sizeof(int)*k);for(int i = 0;i < k;i++){(*result)[(*returnSize)-1][i] = num[i];}*returnColumnSizes = realloc(*returnColumnSizes,(*returnSize)*sizeof(int));(*returnColumnSizes)[(*returnSize)-1] = k;}return;}for(int i = start;i <= 9;i++){sum += i;num[combinesize] = i;travelback(k,n,i+1,num,combinesize+1,result,returnSize,returnColumnSizes,sum);sum -= i;}
}
int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {*returnSize = 0;*returnColumnSizes = NULL;int** result = NULL;int* num = malloc(sizeof(int)*k);int sum = 0;travelback(k,n,1,num,0,&result,returnSize,returnColumnSizes,sum);return result;
}
17.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
| 1 | 2 abc | 3 def |
|---|---|---|
| 4 ghi | 5 jkl | 6 mno |
| 7 pqrs | 8 tuv | 9 wxyz |
| *+ | 0 - | # ↑ |
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
思路:
解答:
/*** Note: The returned array must be malloced, assume caller calls free().*/
void travelback(const char* digits, int* returnSize, const char** a, int index, char** result, char* num) {if (index == strlen(digits)) {num[index] = '\0'; result[(*returnSize)] = malloc((strlen(num) + 1) * sizeof(char)); strcpy(result[*returnSize], num);(*returnSize)++;return;}int digit = digits[index] - '0';const char* letter = a[digit];for (int i = 0; i < strlen(letter); i++) {num[index] = letter[i];travelback(digits, returnSize, a, index + 1, result, num);}
}
char** letterCombinations(char* digits, int* returnSize) {const char* a[10] = {" ", " ", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};if (digits == NULL || strlen(digits) == 0) {*returnSize = 0;return NULL;}int len = strlen(digits);int maxSize = 1;for (int i = 0; i < len; i++) {int digit = digits[i] - '0';if (digit >= 2 && digit <= 9) {maxSize *= strlen(a[digit]);}}*returnSize = 0;char* num = (char*)malloc((len + 1) * sizeof(char)); char** result = (char**)malloc(maxSize * sizeof(char*));travelback(digits, returnSize, a, 0, result, num);free(num); return result;
}
注意:
num[index] = '\0’一定要放在最上面,因为调用 malloc((strlen(num) + 1) * sizeof(char)) 的时候,num 并不是一个完整的字符串,因为 num[index] = '\0'; 还没有设置。strlen(num) 计算长度时会从 num 的开头开始寻找 '\0',但由于它还未设置,因此 strlen(num) 可能返回一个不正确的长度值(可能是过大或过小)。
反思
今天的题目很有难度,有些题目需要多次理解,但是今天对于回溯算法有了一定的理解,还需要多练。
相关文章:

代码随想录第二十二天
回溯算法理论介绍 回溯算法是一种基于递归思想的算法设计技术,适用于解决需要构造所有解或找到特定解的组合问题。回溯的基本思路是通过系统地搜索所有可能的解决方案,然后逐步撤销不符合要求的选择,回到上一步继续尝试。这种算法最适合应用…...

【k8s】ClusterIP能http访问,但是不能ping 的原因
ClusterIP 服务在 Kubernetes 中是可以访问的,但通常无法通过 ping 命令来测试连通性。这主要是因为 ClusterIP 是一个虚拟 IP 地址,而不是实际分配给某个网络接口的 IP 地址。以下是一些原因和解释: 1. 虚拟 IP 地址 ClusterIP 是一个虚拟…...

【力扣打卡系列】单调栈
坚持按题型打卡&刷&梳理力扣算法题系列,语言为go,Day20 单调栈 题目描述 解题思路 单调栈 后进先出 记录的数据加在最上面丢掉数据也先从最上面开始 单调性 记录t[i]之前会先把所有小于等于t[i]的数据丢掉,不可能出现上面大下面小的…...

使用docker安装zlmediakit服务(zlm)
zlmediakit安装 zlmediakit安装需要依赖环境和系统配置,所以采用docker的方式来安装不容易出错。 docker pull拉取镜像(最新) docker pull zlmediakit/zlmediakit:master然后先运行起来 sudo docker run -d -p 1935:1935 -p 80:80 -p 8554:554 -p 10000:10000 -p …...

SOLID原则-单一职责原则
转载请注明出处:https://blog.csdn.net/dmk877/article/details/143447010 作为一名资深程序员越来越感觉到基础知识的重要性,比如设计原则、设计模式、算法等,这些知识的长期积累会让你突破瓶颈实现质的飞跃。鉴于此我决定写一系列与此相关的博客&…...

Transformer究竟是什么?预训练又指什么?BERT
目录 Transformer究竟是什么? 预训练又指什么? BERT的影响力 Transformer究竟是什么? Transformer是一种基于自注意力机制(Self-Attention Mechanism)的神经网络架构,它最初是为解决机器翻译等序列到序列(Seq2Seq)任务而设计的。与传统的循环神经网络(RNN)或卷…...

Jdbc批处理功能和MybatisPlus
文章目录 1. 序言2. JDBC批处理功能和rewriteBatchedStatements3. JDBC批量插入的测试4. MybatisPlus#ServiceImpl.saveBatch()5. 结语:如果对大家有帮助,请点赞支持。如果有问题随时在评论中指出,感谢。 1. 序言 MybatisPlus的ServiceImpl类…...

对于相对速度的重新理解
狭义相对论速度合成公式如下, 现在让我们尝试用另一种方式把它推导出来。 我们先看速度的定义, 常规的速度合成方式如下, 如果我们用速度的倒数来理解速度, 原来的两个相对速度合成, 是因为假定了时间单位是一样的&am…...
默认访问权限)
Scala的属性访问权限(一)默认访问权限
//eg:银行账户存钱取钱 // 账户类: // -balance() 余额 // -deposit() 存钱 // -withdraw() 取钱 // -transfer(to:账户,amount:Dobule)转账 package Test1104 //银行账户class BankAccount(private var balance:Int){def showMoney():Unit {println(s"…...

【算法】(Python)贪心算法
贪心算法: 又称贪婪算法,greedy algorithm。贪心地追求局部最优解,即每一步当前状态下最优选择。试图通过各局部最优解达到最终全局最优解。但不从整体最优上考虑,不一定全局最优解。步骤:从初始状态拆分成一步一步的…...

条件logistic回归原理及案例分析
前面介绍的二元、多分类、有序Logistic回归都属于非条件Logistic回归,每个个案均是相互独立关系。在实际研究中,还有另外一种情况,即个案间存在配对关系,比如医学研究中配对设计的病例对照研究,此时违反了个案相互独立…...
redis7学习笔记
文章目录 1. 简介1.1 功能介绍1.1.1 分布式缓存1.1.2 内存存储和持久化(RDBAOF)1.1.3 高可用架构搭配1.1.4 缓存穿透、击穿、雪崩1.1.5 分布式锁1.1.6 队列 1.2 数据类型StringListHashSetZSetGEOHyperLogLogBitmapBitfieldStream 2. 命令2.1 通用命令copydeldumpexistsexpire …...
)
重学Android:自定义View基础(一)
前言 作为一名安卓开发,也被称为大前端,做一个美观的界面,是我们必备的基础技能,可能在开发中我们最常用的是系统自带的View,因为他能满足绝大部分需求,难一点的我们也可以上Github上找个三方库使用&#…...

前端好用的网站分享——CSS(持续更新中)
1.CSS Scan 点击进入CSS Scan CSS盒子阴影大全 2.渐变背景 点击进入color.oulu 3.CSS简化压缩 点击进入toptal 4.CSS可视化 点击进入CSS可视化 这个强推,话不多说,看图! 5.Marko 点击进入Marko 有很多按钮样式 6.getwaves 点击进入getwaves 生…...
华为HarmonyOS借助AR引擎帮助应用实现虚拟与现实交互的能力3-获取设备位姿
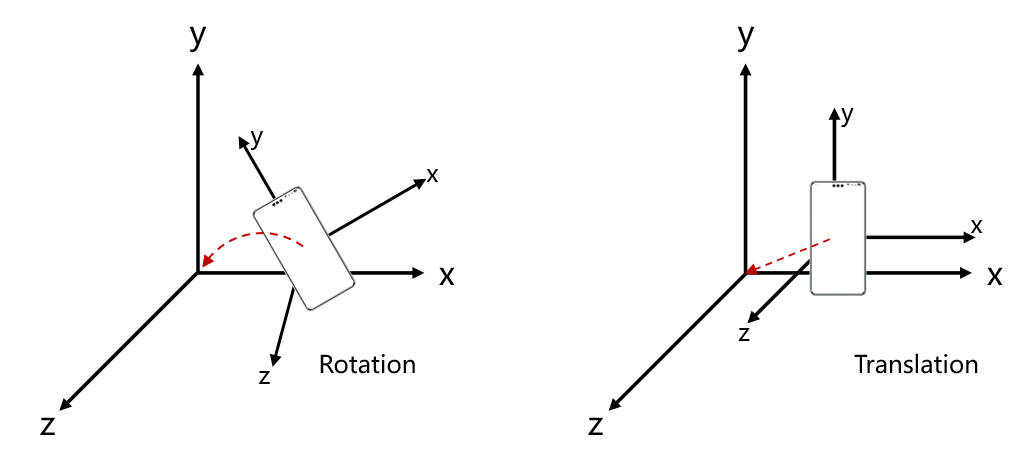
设备位姿描述了物体在真实世界中的位置和朝向。AR Engine提供了世界坐标下6自由度(6DoF)的位姿计算,包括物体的位置(沿x、y、z轴方向位移)和朝向(绕x、y、z轴旋转)。通过AR Engine,您…...

qt QColorDialog详解
1、概述 QColorDialog是Qt框架中的一个对话框类,专门用于让用户选择颜色。它提供了一个标准的颜色选择界面,其中包括基本的颜色选择器(如调色板和颜色轮)、自定义颜色输入区域以及预定义颜色列表。QColorDialog支持RGB、HSV和十六…...

【测试小白--如何写好测试用例--测试用例编写的方法+结合常见登录模块为实例--保姆级教学】
测试用例编写方法&登录模块实例 一、测试用例编写方法1. 等价类划分2. 边界值分析3. 状态转换测试4. 决策表测试5. 错误推测6. 用户场景测试7. 安全测试用例 二、登录模块测试用例实例1. 等价类划分2. 边界值分析3. 状态转换测试4. 决策表测试5. 错误推测6. 用户场景测试7.…...

真题--数组循环题目
1.逆序数表达数组2.用数组表示费波纳希数列3.用数组排序4.二维数组转置5.找到二维数组其中的最大数值6.输出字符数组7.字符数组输出菱形图案8.输入一行字符,统计有多少单词9.有三个字符串,找到最大字符串 1.逆序数表达数组 #include<stdio.h> int…...

【Linux系列】在Linux下安装微信
文章目录 前言一、通用Linux系统使用Flatpak安装(推荐)1. 安装flatpak2. 安装微信 二、国产Linux 前言 此前,微信的Linux版一直在内测阶段,只有在国产的Linux系统和Debian系系统上可以正常安装,如果有心细的好伙伴应该…...

还在使用ElementUI不如试一试DaisyUI,DaisyUI: Tailwind CSS 的高效组件库,
DaisyUI: Tailwind CSS 的高效组件库 daisyUI官网:https://daisyui.com/ 在现代网页开发中,快速构建美观且响应式的用户界面是每个开发者追求的目标。Tailwind CSS 是一个流行的实用程序优先的 CSS 框架,它允许开发者直接在 HTML 中使用预…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
