jenkins 构建报错 Cannot run program “sh”

原因
在 windows 操作系统 jenkins 自动化部署的时候, 由于自动化构建的命令是 shell 执行的,而默认windows 从 path 路径拿到的 shell 没有 sh.exe ,因此报错。
解决方法
前提是已经安装过 git
WIN+R 输入cmd 打开命令行, 然后输入where git 获取 git 的路径, 然后通过路径打开 git 目录, 打开bin文件夹, 找到sh.exe, 然后复制绝对路径,例:E:\Git\bin\sh.exe

填写 sh 路径 ,保存即可

相关文章:

jenkins 构建报错 Cannot run program “sh”
原因 在 windows 操作系统 jenkins 自动化部署的时候, 由于自动化构建的命令是 shell 执行的,而默认windows 从 path 路径拿到的 shell 没有 sh.exe ,因此报错。 解决方法 前提是已经安装过 git WINR 输入cmd 打开命令行, 然后输入where git 获取 git 的路径, …...
Netty ByteBuf 分配 | 池化复用 、直接内存
Netty ByteBuf 分配 本文主要内容关于 ByteBuf 分配介绍,为了更好的理解本文,我们可以带着几个问题思考 在IO密集型业务场景下,可能涉及大量ByteBuf分配,这时我们需 要考虑会不会产生OOM会不会出现频繁GC会不会内存泄露 根据上…...

【数据结构】堆和二叉树(2)
文章目录 前言一、建堆和堆排序1.堆排序 二、二叉树链式结构的实现1.二叉树的遍历 三、链式二叉树的功能函数1.二叉树结点个数2.二叉树叶子结点个数3.二叉树的高度4.二叉树第k层结点个数5. 二叉树查找值为x的结点6.二叉树销毁 总结 前言 接着上一篇博客,我们继续分…...

Oracle分区技术特性
Oracle 的分区是一种“分而治之”的技术,通过将大表、索引分成可以独立管理的、小的 Segment,从而避免了对每个对象作为一个大的、单独的 Segment 进行管理,为海量数据访问提供了可伸缩的性能。自从 Oracle 引入分区技术以来,Orac…...

Hive操作库、操作表及数据仓库的简单介绍
数据仓库和数据库 数据库和数仓区别 数据库与数据仓库的区别实际讲的是OLTP与OLAP的区别 操作型处理(数据库),叫联机事务处理OLTP(On-Line Transaction Processing),也可以称面向用户交易的处理系统,它是针对具体业务…...

智能网联汽车:人工智能与汽车行业的深度融合
内容概要 在这个快速发展的时代,智能网联汽车已经不再是科幻电影的专利,它正在悄然走进我们的日常生活。如今,人工智能(AI)技术与汽车行业的结合犹如一场科技盛宴,让我们看到了未来出行的新方向。通过自动…...

VUE 循环的使用方法集锦
vue---循环方式以及跳出循环 在做VUE项目开发过程中,数据循环是常见的操作方式,以下是几种常见的数据循环方式: 一、for循环 let data [1,2,3,4,5,6,7,8,9,10]; for(let i0; i<data.length; i){console.log(data[i]);if(i>5){break;…...

Centos部署资料
1. 离线rpm 1.1 下载地址: 阿里云rpmfind 1.2 本地安装: [rootlocalhost ~]# yum localinstall unzip-6.0-21.el7.x86_64.rpm2. 服务器操作 2.1 修改网络ip [rootlocalhost ~]# cd /etc/sysconfig/network-scripts/ [rootlocalhost network-script…...

AI之硬件对比:据传英伟达Nvidia2025年将推出RTX 5090-32GB/RTX 5080-24GB、华为2025年推出910C/910D
AI之硬件对比:据传英伟达Nvidia2025年将推出RTX 5090-32GB/RTX 5080-24GB、华为2025年推出910C/910D 目录 Nvidia的显卡 Nvidia的5090/5080/4090/4080:据传传英伟达Nvidia RTX 5090后续推出32GB版且RTX 5080后续或推出24GB版 RTX 5090相较于RTX 4090&…...

其他节点使用kubectl访问集群,kubeconfig配置文件 详解
上述两种方式:可使用kubectl连接k8s集群。 $HOME/.kube/config 是config文件默认路径,要么直接定义环境变量,要么就直接把文件拷过去 config文件里面,定义了context,里面指定了用户和对应的集群信息: ku…...

【鉴权】深入解析OAuth 2.0:访问令牌与刷新令牌的安全管理
目录 引言一、访问令牌(Access Token)1.1 访问令牌概述1.2 访问令牌的格式1.2.1 JWT(JSON Web Token)1.2.1.1 JWT 结构1.2.1.2 示例 JWT 1.2.2 Bearer Token 1.3 访问令牌的有效期1.4 访问令牌的工作流程 二、刷新令牌(…...

【AI视频换脸整合包及教程】AI换脸新星:Rope——让换脸变得如此简单
在数字技术迅猛发展的今天,人工智能(AI)的应用已经渗透到了我们生活的方方面面,从日常的语音助手到复杂的图像处理,无不体现着AI技术的魅力。特别是在娱乐和创意领域,AI技术更是展现出了惊人的潜力。其中&a…...
)
限界上下文(Bounded Context)
限界上下文(Bounded Context):领域驱动设计中的重要概念 在领域驱动设计(Domain-Driven Design, DDD)中,限界上下文(Bounded Context)是一个非常重要的概念。限界上下文定义了一个特定领域模型的边界,确保在这个边界内,领域模型的术语、规则和逻辑是一致的。通过明确…...

20241105专家访谈学习资料
“两性一度” 即高阶性、创新性、挑战度。“三性一度”是指教学目标的适应性、教学内容的先进性、教学实施的实践性及教学评价的有效度。“四性一度”是指系统性、层次性、前瞻性、专业性以及培养目标达成度。“二性一度”用词比较规范、标准统一,“三性一度”和“四…...

Docling:开源的文档解析工具,支持多种格式的解析和转换,可与其他 AI 工具集成
❤️ 如果你也关注大模型与 AI 的发展现状,且对大模型应用开发非常感兴趣,我会快速跟你分享最新的感兴趣的 AI 应用和热点信息,也会不定期分享自己的想法和开源实例,欢迎关注我哦! 🥦 微信公众号ÿ…...

oracle如何在不同业务场景下正确使用聚合查询、联合查询及分组查询?
引言 在数据库管理系统中,SQL(结构化查询语言)是用于与数据库进行交互的标准语言。 Oracle数据库作为一种广泛使用的关系数据库管理系统,提供了丰富的SQL功能,包括聚合查询、联合查询和分组查询等。 这些功能在数据…...

Hearts of Iron IV 之 Archive Modification
存档位置 C:\Users\XXX\Documents\Paradox Interactive\Hearts of Iron IV\save games 打开文档 打开C:\Users\XXX\Documents\Paradox Interactive\Hearts of Iron IV\settings.txt,将save_as_binaryyes 改成save_as_binaryno,然后退出游戏重新存档&a…...

python manage.py下的命令及功能
python manage.py 是 Django 框架中用于管理 Django 项目的命令行工具 1、startapp: 功能:创建一个新的 Django 应用程序。 用法:python manage.py startapp appname 示例:python manage.py startapp blog 2、startproject&a…...

建筑行业员工离职SOP的数字化管理
在建筑行业,随着数字化转型的深入,对员工离职的标准操作程序(SOP)进行数字化管理变得尤为重要。这不仅有助于提高管理效率,还能确保离职流程的规范性和合规性。本文将探讨建筑行业如何通过数字化手段管理员工离职SOP&a…...
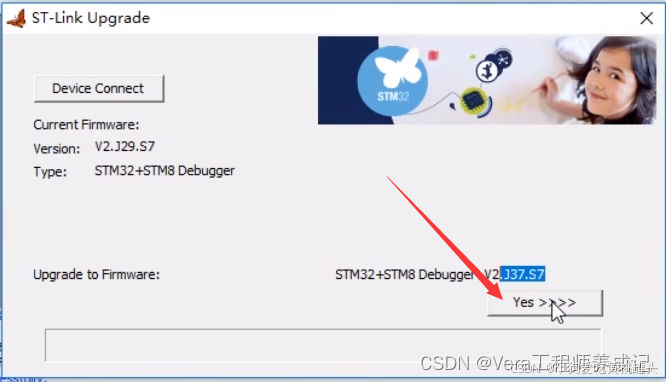
江协科技STM32学习- P30 FlyMCU串口下载STLink Utility
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
