【MATLAB源码-第210期】基于matlab的OFDM电力线系统仿真,不同梳状导频间隔对比。三种信道估计,三种插值误码率对比
操作环境:
MATLAB 2022a
1、算法描述
OFDM电力线通信系统(PLC)是一种通过电力线传输数据的通信技术,利用了OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)技术的优势来提高数据传输的速率和质量。电力线作为一种传输介质,其特点包括信道条件的不稳定性、高衰减率以及严重的多径效应。因此,为了保证通信的可靠性和效率,信道估计技术在OFDM电力线通信系统中扮演着至关重要的角色。
OFDM技术简介
OFDM技术通过将一个高速数据流分割成多个低速数据流,分别在多个正交的子载波上并行传输,有效地利用了频谱资源,同时减少了频率选择性衰落的影响。每个子载波之间通过正交性相互隔离,减少了互相干扰。为了进一步降低多径效应带来的影响,OFDM系统通常会在每个OFDM符号前加入循环前缀(CP),以消除符号间干扰(ISI)和子载波间干扰(ICI)。
电力线通信(PLC)的特点
电力线作为通信信道,具有一些独特的挑战,如信道的时变性、高衰减和强烈的多径效应。这些特点要求PLC系统必须具备高度的适应性和鲁棒性。OFDM技术的引入,以其高效的频谱利用率和对多径干扰的强韧性,成为PLC系统的理想选择。
信道估计的重要性
在OFDM系统中,信道估计的目的是在接收端估计出信道的冲击响应,以便对接收到的信号进行适当的处理,从而恢复出发送端的原始数据。准确的信道估计能够显著提高数据恢复的准确性,降低误码率,从而提高通信系统的整体性能。
主要信道估计算法
最小二乘法(Least Squares, LS)
LS算法是基于最小化接收信号与通过信道模型估计的信号之间差异的平方和来进行信道估计。它的主要优点是实现简单,计算量较小。然而,LS估计受噪声的影响较大,特别是在低信噪比的环境下,其性能会显著下降。
最小均方误差(Minimum Mean Square Error, MMSE)
MMSE算法通过考虑噪声的统计特性来最小化估计信号和实际信号之间的均方误差。与LS算法相比,MMSE算法在低信噪比环境下提供了更好的性能,但代价是计算复杂度更高。
奇异值分解(Singular Value Decomposition, SVD)
SVD算法通过对信号矩阵进行分解,提取出信道信息。这种方法在处理信道相关性和噪声条件下具有优异的性能,但计算复杂度相对较高,特别是在子载波数量较多的情况下。
插值算法的应用
在OFDM系统中,通常只在部分子载波上插入已知的导频信号来进行信道估计,然后通过插值算法在整个频带上恢复信道的估计值,这样可以减少计算量和系统开销。
线性插值(Linear Interpolation)
线性插值是最简单的插值方法,它通过直线连接两个已知点来估计这两点之间的值。尽管实现简单,但在信道变化较为复杂的情况下,线性插值的精度可能不足。
三次样条插值(Cubic Spline Interpolation)
三次样条插值通过多个三次多项式片段在每两个导频之间进行拟合,每个片段的边界条件保证了整个函数的二阶导数连续,从而在整个频带上形成一条平滑的曲线。相比线性插值,样条插值能够更准确地估计信道特性,尤其是在信道特性变化较平滑的情况下。
变换域DFT插值
变换域DFT插值方法基于离散傅里叶变换的性质,在频域进行插值。这种方法尤其适用于信道特性在频域内有明显规律变化的情况。通过在频域进行插值,可以有效地恢复出整个信道的频率响应,从而在时域得到准确的信道估计值。
结论
OFDM电力线通信系统通过利用OFDM技术的高效频谱利用率和对多径干扰的鲁棒性,解决了电力线作为通信介质所固有的挑战。在此基础上,信道估计技术和插值算法的合理选择和应用,进一步提升了系统的性能,确保了数据传输的准确性和可靠性。未来,随着算法优化和计算能力的提高,OFDM电力线通信系统有望在智能电网、家庭网络等领域得到更广泛的应用。
2、仿真结果演示

3、关键代码展示
略
4、MATLAB 源码获取
点击下方原文链接获取
【MATLAB源码-第210期】基于matlab的OFDM电力线系统仿真,不同梳状导频间隔对比。三种信道估计,三种插值误码率对比_导频内插方法linear spline-CSDN博客![]() https://blog.csdn.net/Koukesuki/article/details/139007036?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522CF1BA01D-DCBB-46FD-B2F7-73C07AB23E47%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=CF1BA01D-DCBB-46FD-B2F7-73C07AB23E47&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-139007036-null-null.nonecase&utm_term=210&spm=1018.2226.3001.4450
https://blog.csdn.net/Koukesuki/article/details/139007036?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522CF1BA01D-DCBB-46FD-B2F7-73C07AB23E47%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=CF1BA01D-DCBB-46FD-B2F7-73C07AB23E47&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-139007036-null-null.nonecase&utm_term=210&spm=1018.2226.3001.4450
相关文章:
【MATLAB源码-第210期】基于matlab的OFDM电力线系统仿真,不同梳状导频间隔对比。三种信道估计,三种插值误码率对比
操作环境: MATLAB 2022a 1、算法描述 OFDM电力线通信系统(PLC)是一种通过电力线传输数据的通信技术,利用了OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)技术的优势来提高…...

基于SpringBoot的城镇保障性住房管理策略
3系统分析 3.1可行性分析 通过对本城镇保障性住房管理系统实行的目的初步调查和分析,提出可行性方案并对其一一进行论证。我们在这里主要从技术可行性、经济可行性、操作可行性等方面进行分析。 3.1.1技术可行性 本城镇保障性住房管理系统采用SSM框架,JA…...

支持高性能结构化数据提取的 Embedding 模型——NuExtract-v1.5
NuExtract 是一个用户友好型模型,设计用于从长文档中提取信息。它可以处理长达 20,000 个标记的输入,是合同、报告和其他商业通信的理想选择。NuExtract 的与众不同之处在于它能够处理和理解文档的整个上下文。这意味着它可以捕捉到可能分散在长文本不同…...

【C#】设计一个选购计算机配置的应用程序
文章目录 1. 创建新的 Windows Forms 应用程序项目2. 设计界面2.1 添加控件和设置属性 3. 编写事件处理代码4. 运行和测试应用程序 1. 创建新的 Windows Forms 应用程序项目 打开 Visual Studio。选择“创建新项目”。在项目类型中选择“Windows Forms 应用程序”(…...

solo博客源码使用idea编译运行
solo博客源码使用idea编译运行 solo博客开源地址本地运行IDEA 编译执行默认直接编译jar 包编译 solo博客开源地址 项目地址:GitHub - 88250/solo: 🎸 B3log 分布式社区的 Java 博客端节点系统,欢迎加入下一代社区网络。B3log distributed co…...

VBA07-方法
一、方法的定义 方法指对象所能执行的动作,它是一个动词。 二、方法的表达方式 三、关于工作簿的方法操作 3-1、新增一个工作簿 示例1: 此时,新增的工作簿的名字是系统默认的。 示例2: 【注意】: 当你尝试将工作簿…...

spring boot 统一异常处理
在 Spring Boot 应用中实现统一异常处理是非常重要的,它可以帮助我们更好地管理和响应应用程序中的错误。通过使用 ControllerAdvice 和 ExceptionHandler 注解,我们可以创建一个全局的异常处理器来捕获并处理不同类型的异常。 步骤 1: 创建一个异常处理…...
——神经网络的基本骨架(nn.model))
跟着小土堆学习pytorch(六)——神经网络的基本骨架(nn.model)
文章目录 一、model介绍二、Module三、张量3.1 定义3.2 用法 一、model介绍 容器 Containers 卷积层 Convolution Layers 池化层 Pooling layers 填…...

数字化落地过程中的研发效能治理如何开展?
数字化落地过程中,针对数字化识别到的问题和短板进行专项治理,是通过数字化手段持续提升研发效能非常重要的一环。组织级的数字化专项治理需要组织级团队和技术团队共同配合协同来完成。其中组织级团队负责制定整体的治理目标、流程和策略,根…...

Windows安装配置node.js
下载安装 下载 访问下载 | Node.js 中文网,下载 推荐使用长期支持版本,但是此次是学习用的,使用最新版本试一下 安装 其实一路next基本就可以了,注意调整下安装目录 查看版本 C:\Users\PC>node -v v22.11.0 C:\Users\PC>…...

Javaweb梳理9——JDBC
Javaweb梳理9——JDBC 1.JDBC概述1.1 JDBC概念1.2 JDBC本质1.3 JDBC好处 2.JDBC快速入门2.1 编写代码步骤2.2 具体操作 3 JDBC API详解3.1 DriverManager3.2 Connection3.2.1 获取执行对象3.2.2 事务管理 3.3 Statement3.3.1 概述3.3.2 代码实现 3.4 ResultSet3.4.1 概述3.4.2 …...
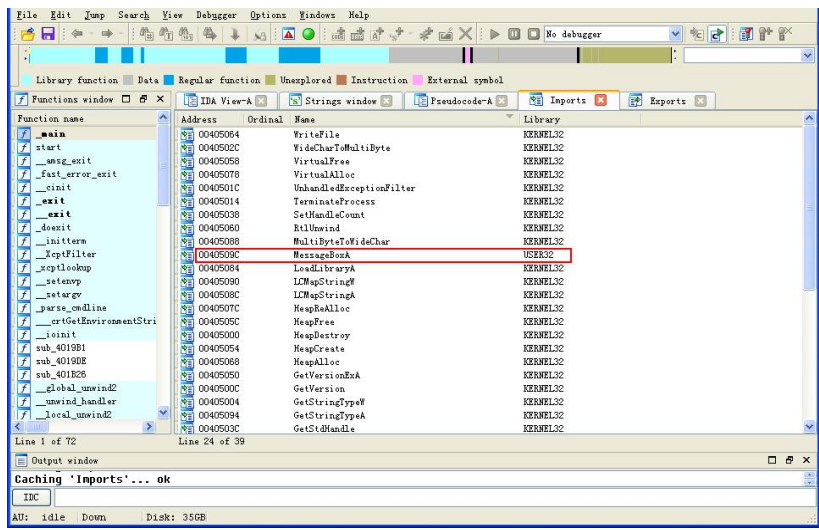
逆向CTF入门(如何找main)
Hello, world of reverse! start函数它在执行一些初始化操作,如获取命令行参数、获取环境变量值、初始化全局变量等,一切准备工作完成之后,再调用main函数 快速定位关键函数: 长驱直入法:当程序功能非常明确时,从程序…...

c语言归并排序
归并排序思想: 归并排序可以解释为是将放在数组里的一串数字进行拆分,拆分之后再判断大小合并的过程,每次都是从中间位置拆分,例如有七个数,第一次拆分就将它们分成前三个数为一个数组,后四个数为一个数组&…...

碳化硅陶瓷膜的特性
无机膜包括金属膜、陶瓷膜、玻璃膜等等,其中在水处理领域里出镜最多、应用最广的当属陶瓷膜。比起高分子有机膜,陶瓷膜硬度更高、通量更大、寿命更长,然其性能优越,成本也很“高昂”,故其生存空间自然是受到高分子有机…...

机器学习(三)——决策树(附核心思想、重要算法、概念(信息熵、基尼指数、剪枝处理)及Python源码)
目录 关于1 基本流程2 划分属性的选择2.1 方法一:依据信息增益选择2.2 方法二:依据增益率选择2.3 方法三:依据基尼指数选择 3 剪枝处理:防止过拟合3.1 预剪枝3.2 后剪枝 4 连续与缺失值4.1 连续值处理4.2 缺失值处理 5 多变量决策…...

良心无广,这五款电脑软件堪称必备,最后一个比快播都猛
来吧,直接上狠货! 哔哔音乐 这是一个基于哔哩哔哩开发的电脑听歌软件,众所周知!B站其实就是一个巨大的曲库,啥歌各种版本都能在这里找到。 所以如果依托B站开发听歌软件,那就是真的香,而且软件…...

Vue3中实现原生CSS完成圆形按钮点击粒子效果和定点旋转动画
效果: 源码: <script setup> import { ElMessage } from "element-plus"; const isClick () > {ElMessage.success(Clicked); }; </script><template><button click"isClick" class"button">…...

百度网盘 服务器开小差了
有会员,新上传文件到百度网盘,分享链接, 别人打开链接,显示【服务器开小差了,请稍后重试~】,保存不了 试了几个都不行,文件是视频MP4 可行的方法是百度网盘加好友,然后在聊天页面单…...

数据分析师招聘要求
在当今数据驱动的世界中,数据分析师的角色变得愈发重要,他们被赋予从海量数据中提炼洞察的关键任务。数据分析师的招聘要求反映了这个职位多方面的需求,从教育背景到技能,再到软技能和行业特有的知识。本文将详细探讨这些要求&…...

【C语言】实战-力扣题库:回文链表
题目描述 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 提示: 链表中节点数目在范围[1, 105] 内0 < Node.val < 9 进阶:你能否用 O(n) 时间…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
