LeetCode题练习与总结:打乱数组--384
一、题目描述
给你一个整数数组 nums ,设计算法来打乱一个没有重复元素的数组。打乱后,数组的所有排列应该是 等可能 的。
实现 Solution class:
Solution(int[] nums)使用整数数组nums初始化对象int[] reset()重设数组到它的初始状态并返回int[] shuffle()返回数组随机打乱后的结果
示例 1:
输入 ["Solution", "shuffle", "reset", "shuffle"] [[[1, 2, 3]], [], [], []] 输出 [null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]解释 Solution solution = new Solution([1, 2, 3]); solution.shuffle(); // 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。例如,返回 [3, 1, 2] solution.reset(); // 重设数组到它的初始状态 [1, 2, 3] 。返回 [1, 2, 3] solution.shuffle(); // 随机返回数组 [1, 2, 3] 打乱后的结果。例如,返回 [1, 3, 2]
提示:
1 <= nums.length <= 50-10^6 <= nums[i] <= 10^6nums中的所有元素都是 唯一的- 最多可以调用
10^4次reset和shuffle
二、解题思路
为了实现这个功能,我们可以使用Fisher-Yates洗牌算法来确保每个元素在每个位置的概率都是相等的。
三、具体代码
import java.util.Random;class Solution {private int[] original;private int[] shuffled;private Random rand;public Solution(int[] nums) {original = nums.clone(); // 复制一份原始数组shuffled = nums.clone(); // 初始化打乱数组rand = new Random(); // 初始化随机数生成器}public int[] reset() {// 重置数组到初始状态return original.clone();}public int[] shuffle() {// 使用Fisher-Yates洗牌算法打乱数组for (int i = shuffled.length - 1; i > 0; i--) {int index = rand.nextInt(i + 1); // 生成一个[0, i]范围内的随机数// 交换当前元素与随机选中的元素int temp = shuffled[index];shuffled[index] = shuffled[i];shuffled[i] = temp;}return shuffled;}
}/*** Your Solution object will be instantiated and called as such:* Solution obj = new Solution(nums);* int[] param_1 = obj.reset();* int[] param_2 = obj.shuffle();*/
在这个实现中,我们维护了两个数组:original用于存储初始状态,shuffled用于存储打乱后的状态。reset方法返回original数组的副本,而shuffle方法则使用Fisher-Yates算法打乱shuffled数组,并返回打乱后的结果。
Fisher-Yates算法的工作原理是从数组的最后一个元素开始,随机选择一个元素与之交换,然后逐步向前处理,直到处理到数组的第一个元素。这样每个元素都有相同的机会出现在数组的任何位置。
四、时间复杂度和空间复杂度
1. 时间复杂度
-
构造函数
Solution(int[] nums):nums.clone():这个操作的时间复杂度是 O(n),其中 n 是数组nums的长度。- 初始化
Random对象:这个操作的时间复杂度是 O(1)。 因此,构造函数的总时间复杂度是 O(n)。
-
reset()方法:original.clone():这个操作的时间复杂度是 O(n),因为需要复制整个原始数组。 因此,reset()方法的时间复杂度是 O(n)。
-
shuffle()方法:- Fisher-Yates 洗牌算法:这个算法包含一个从后向前的循环,循环体内有一个交换操作。循环的次数是 n-1(其中 n 是数组的长度),每次循环中的交换操作是 O(1)。 因此,
shuffle()方法的时间复杂度是 O(n)。
- Fisher-Yates 洗牌算法:这个算法包含一个从后向前的循环,循环体内有一个交换操作。循环的次数是 n-1(其中 n 是数组的长度),每次循环中的交换操作是 O(1)。 因此,
2. 空间复杂度
-
构造函数
Solution(int[] nums):original和shuffled数组:每个数组都需要 O(n) 的空间来存储数组的副本。rand对象:这个对象的空间复杂度是 O(1)。 因此,构造函数的总空间复杂度是 O(n)。
-
reset()方法:- 返回的是
original数组的副本,但这个副本是在方法外部创建的,所以方法本身不占用额外的空间。 因此,reset()方法的时间复杂度是 O(1)。
- 返回的是
-
shuffle()方法:- 方法内部只使用了常数额外空间(用于交换元素时的临时变量
temp)。 因此,shuffle()方法的时间复杂度是 O(1)。
- 方法内部只使用了常数额外空间(用于交换元素时的临时变量
3. 总结
- 时间复杂度:构造函数和
shuffle()方法都是 O(n),reset()方法也是 O(n)。 - 空间复杂度:构造函数是 O(n),
reset()方法和shuffle()方法都是 O(1)。
五、总结知识点
-
类定义:
class关键字用于定义一个类。- 类名
Solution是自定义的,代表这个类的名称。
-
成员变量:
private关键字用于定义类的私有成员变量,确保这些变量只能在类的内部访问。int[] original和int[] shuffled分别用于存储原始数组和打乱后的数组。Random rand是java.util.Random类的一个实例,用于生成随机数。
-
构造函数:
- 构造函数
Solution(int[] nums)用于初始化类的实例。 nums.clone()方法用于创建原始数组的副本。
- 构造函数
-
方法定义:
public关键字用于定义公共方法,这些方法可以被类的外部访问。int[] reset()和int[] shuffle()是两个公共方法,分别用于重置数组和打乱数组。
-
数组操作:
- 数组克隆:使用
.clone()方法复制数组。 - 数组元素交换:通过临时变量
int temp来交换数组中的两个元素。
- 数组克隆:使用
-
随机数生成:
Random类的实例rand用于生成随机数。rand.nextInt(i + 1)方法用于生成一个介于[0, i]范围内的随机整数。
-
Fisher-Yates洗牌算法:
shuffle()方法实现了Fisher-Yates洗牌算法,这是一种高效的随机打乱数组的方法。- 算法从数组的最后一个元素开始,随机选择一个元素与之交换,然后逐步向前处理,直到处理到数组的第一个元素。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:打乱数组--384
一、题目描述 给你一个整数数组 nums ,设计算法来打乱一个没有重复元素的数组。打乱后,数组的所有排列应该是 等可能 的。 实现 Solution class: Solution(int[] nums) 使用整数数组 nums 初始化对象int[] reset() 重设数组到它的初始状态并返回int[]…...

科技改变生活:最新智能开关、调光器及插座产品亮相
根据QYResearch调研团队的最新力作《欧洲开关、调光器和插座市场报告2023-2029》显示,预计到2029年,欧洲开关、调光器和插座市场的规模将攀升至57.8亿美元,并且在接下来的几年里,将以4.2%的复合年增长率(CAGRÿ…...

传统RAG流程;密集检索器,稀疏检索器:中文的M3E
目录 传统RAG流程 相似性搜索中:神经网络的密集检索器,稀疏检索器 密集检索器 BGE系列模型 text-embedding-ada-002模型 M3E模型 稀疏检索器 示例一:基于TF-IDF的稀疏检索器 示例二:基于BM25的稀疏检索器 稀疏检索器的特点与优势 传统RAG流程 相似性搜索中:神经…...

基于统计方法的语言模型
基于统计方法的语言模型 基于统计方法的语言模型主要是指利用统计学原理和方法来构建的语言模型,这类模型通过分析和学习大量语料库中的语言数据,来预测词、短语或句子出现的概率。 N-gram模型:这是最基础的统计语言模型之一,它基…...

Flux comfyui 部署笔记,整合包下载
目录 comfyui启动: 1、下载 Flux 模型 2、Flux 库位置 工作流示例: Flux学习资料免费分享 comfyui启动: # 配置下载模型走镜像站 export HF_ENDPOINT="https://hf-mirror.com" python3 main.py --listen 0.0.0.0 --port 8188 vscode 点击 port 映射到本地,…...

高性能分布式缓存Redis-数据管理与性能提升之道
一、持久化原理 Redis是内存数据库,数据都是存储在内存中,为了避免进程退出导致数据的永久丢失,需要定期将Redis中的数据以某种形式(数据或命令)从内存保存到硬盘;当下次Redis重启时,利用持久化文件实现数据恢复。除此…...

BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测
BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测 目录 BO-CNN-LSTM回归预测 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多输入单输出回归预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 …...

DataWind将字符串数组拆出多行的方法
摘要: 可视化建模中先将字符串split为array再用explode(array)即可 可视化建模 进入“可视化建模”页面 1.1 新建任务 如果团队内没有可视化建模任务。请点击“新建任务”,输入名称并确定。 1.2 建立数据连接 在左边栏中选择“数据连接”,…...

try...catch 和then...catch的异同点分析
try…catch 和 then…catch 的异同点分析 在现代 JavaScript 编程中,异常处理和 Promise 的处理是非常常见的两种方式。try...catch 语句主要用于同步代码的异常处理,而 .then().catch() 是 Promise 中的异步处理方法。 1. 基础概念 1.1 try…catch …...
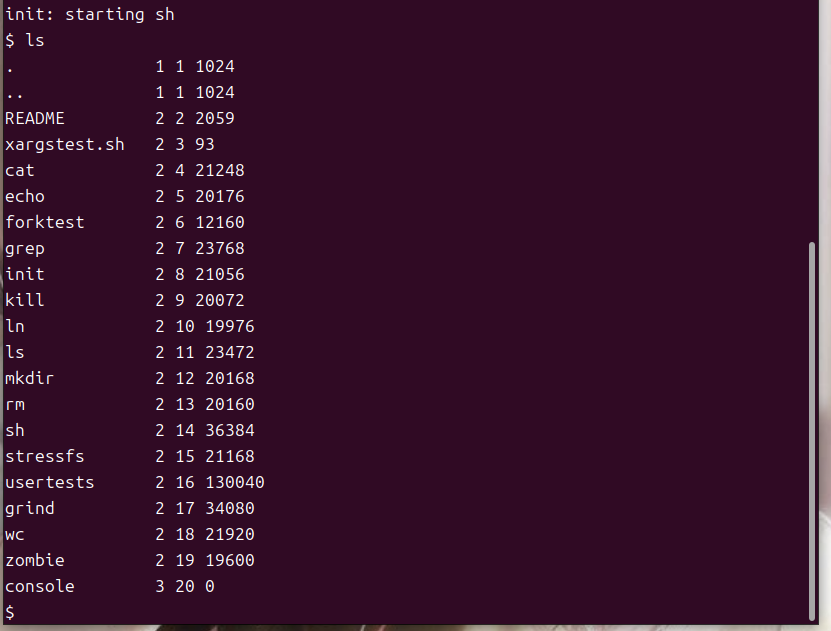
Mit6.S081-实验环境搭建
Mit6.S081-实验环境搭建 注:大家每次做一些操作的时候觉得不太保险就先把虚拟机克隆一份 前言 qemu(quick emulator):这是一个模拟硬件环境的软件,利用它可以运行我们编译好的操作系统。 准备一个Linux系统…...

以太网交换安全:MAC地址漂移
一、什么是MAC地址漂移? MAC地址漂移是指设备上一个VLAN内有两个端口学习到同一个MAC地址,后学习到的MAC地址表项覆盖原MAC地址表项的现象。 MAC地址漂移的定义与现象 基本定义:MAC地址漂移发生在一个VLAN内的两个不同端口学习到相同的MAC地…...

STM32实现串口接收不定长数据
原理 STM32实现串口接收不定长数据,主要靠的就是串口空闲(idle)中断,此中断的触发条件与接收的字节数无关,只有当Rx引脚无后续数据进入时(串口空闲时),认为这时候代表一个数据包接收完成了&…...

AAA 数据库事务隔离级别及死锁
目录 一、事务的四大特性(ACID) 1. 原子性(atomicity): 2. 一致性(consistency): 3. 隔离性(isolation): 4. 持久性(durability): 二、死锁的产生及解决方法 三、事务的四种隔离级别 0 .封锁协议 …...

外接数据库给streamlit等web APP带来的变化
之前我采用sreamlit制作了一个调查问卷的APP, 又使用MongoDB作为外部数据存储,隐约觉得外部数据库对于web APP具有多方面的意义,代表了web APP发展的趋势之一,似乎是作为对这种趋势的响应,streamlit官方近期开发了st.c…...

Gitpod: 我们正在离开 Kubernetes
原文:Christian Weichel - 2024.10.31 Kubernetes 似乎是构建远程、标准化和自动化开发环境的显而易见选择。我们也曾这样认为,并且花费了六年时间,致力于打造最受欢迎的云开发环境平台,并达到了互联网级的规模。我们的用户数量达…...

1.每日SQL----2024/11/7
题目: 计算用户次日留存率,即用户第二天继续登录的概率 表: iddevice_iddate121382024-05-03232142024-05-09332142024-06-15465432024-08-13523152024-08-13623152024-08-14723152024-08-15832142024-05-09932142024-08-151065432024-08-131123152024-…...
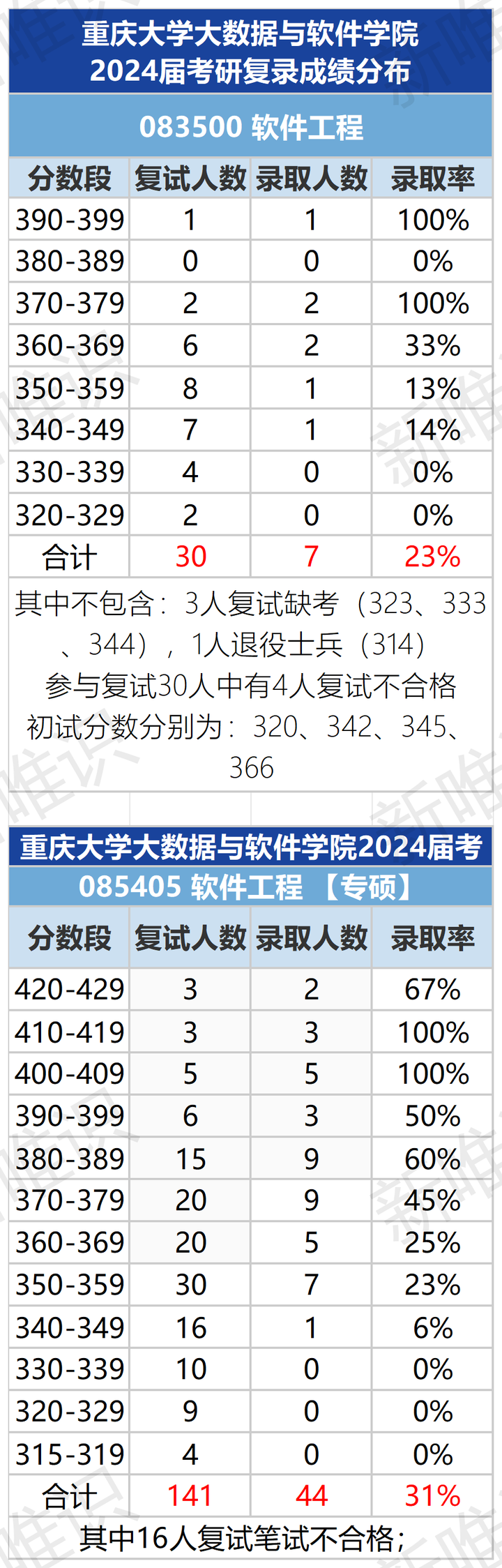
普通一本大二学生,软件工程,想考研985,想知道哪个大学的软件工程好,又不至于完全考不起的?
竞争难度适中:相较于顶尖985院校,重庆大学作为实力派985高校,其竞争烈度较为温和,考研难度适中偏易,为追求高性价比深造路径的考生提供了理想之选。 考试难度友好:重庆地区考研评分标准相对宽松࿰…...

「QT」几何数据类 之 QMatrix4x4 4x4矩阵类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

让Apache正确处理不同编码的文件避免中文乱码
安装了apache2.4.39以后,默认编码是UTF-8,不管你文件是什么编码,统统按这个来解析,因此 GB2312编码文件内的中文将显示为乱码。 <!doctype html> <html> <head><meta http-equiv"Content-Type" c…...

人员密集场所遇到突发火灾事故该如何应对
0引言 在繁华喧嚣的都市中,人员密集场所如购物中心、电影院、办公楼等,是人们日常生活不可或缺的一部分。然而,在这些看似繁华的背后,隐藏着不可忽视的安全隐患——火灾。火灾无情,往往在不经意间爆发,瞬间…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
