LC:二分查找——杂记
文章目录
- 268. 丢失的数字
- 162. 寻找峰值
268. 丢失的数字
LC将此题归类为二分查找,并且为简单题,下面记一下自己对这道题目的思考。
题目链接:268.丢失的数字


第一次看到这个题目,虽然标注的为简单,但肯定不能直接排序或者使用哈希表去实现,如果这样做的话这道题目就没有任何意义。我首先联想到一道剑指offer上面的一道原地哈希的题目,但具体写的时候下笔难。
下面参考宫水三叶的题解,自己重新写一遍。
方法一:原地哈希:
由于题目所述为查找nums[]一共n个数,[0, n]这n + 1个数哪个不存在与数组中。借助nums本体数组,使用原地哈希,每次碰到一个数字,如果不符合nums[i] == i,此时将nums[i]移动到对应numsp[i]的位置上,继续从i开始遍历。
第一遍遍历完成后,再此遍历nums数组,如果碰到nums[i] != i 此时直接返回 i ,否则遍历完毕仍然没有遇到符合要求的数,此时直接返回n。
代码如下所示:
class Solution {public int missingNumber(int[] nums) {// 原地交换int n = nums.length;for(int i = 0; i < n; i++){if(nums[i] != i && nums[i] < n){// 这里为什么要i--,因为这个交换操作只是将nums[i]对应的元素移到了它应该处于的位置nums[i]上,//但原本nums[i]位置的数组却被交换到i位置了,下次遍历需要继续从i位置开始遍历,由于for循环中对i不断++所以这里需要进行-1操作。swap(nums, nums[i], i--);}}for(int i = 0; i < n; i++){if(nums[i] != i){return i;}}return n;}public void swap(int[] nums, int i, int j){int num = nums[i];nums[i] = nums[j];nums[j] = num;}
}方法二:异或操作:
如果做过:【只有一个数字出现1次,其他数字都出现两次】这个题目,相信也可以对题目稍加改造,将其构造为这个题目,具体操作,首先将ans 异或[0, n]随后,遍历nums数组并对ans进行异或操作。这样处理后,最终的ans就是返回答案。
class Solution {public int missingNumber(int[] nums) {//异或int ans = 0, n = nums.length;for(int i = 0; i <= n; i++){ans ^= i;}for(int i = 0; i < n; i++){ans ^= nums[i];}return ans;}
}
方法三:等差数组求和:
由于题目所述为寻找[0, n] 这n + 1个数字在nums中没有出现的数字,先对[0, n]这n + 1个数字使用等差数列求和,计为sum。再遍历nums,对nums中所有数组求和curSum,随后sum - curSum即为最终答案。
代码:
class Solution {public int missingNumber(int[] nums) {int n = nums.length;int curSum = 0, sum = n * (n + 1) / 2;for(int num : nums){curSum += num;}return sum - curSum;}}
162. 寻找峰值
题目链接:162.寻找峰值

这个题目散发出熟悉的味道,之前做过,并且也成功做出来了,但是这次没看题解代码写的比别人题解非常负责,具体可以参考后面写的代码示例。
基本思想:使用二分查找思想,[l, r] 求的mid后,比较nums[mid] 和 nums[mid + 1]的大小关系。(为什么比较nums[mid] 和 nums[mid + 1]而不是比较nums[mid] 和 nums[mid - 1]的大小:Java中向下取整的,保证有两个数的前提下,通过(l + r) / 2 计算出的mid,此时mid + 1一定不会越界的,相反对于mid - 1可能会越界,在只有两个数的情况下就会越界。)
随后根据nums[mid] 和 nums[mid + 1]的大小关系移动左右边界。
- nums[mid] > nums[mid + 1] 此时,mid可以用,并且由于左边数更大,所以边界向左边收缩。r = mid。
- 不满足1,此时mid 是不可用的,此时向右边界收缩,r = mid + 1。
上面思路的前提,nums[-1] == nums[n] = -00。
代码展示:
class Solution {public int findPeakElement(int[] nums) {int len = nums.length;if(len == 1) return 0;int l = 0, r = len - 1;while(l < r){int mid = l + (r - l) / 2;if((mid == 0 && nums[mid] > nums[mid + 1]) || (mid == len - 1 && nums[mid] > nums[mid - 1])){return mid;}if(mid > 0 && mid < len - 1 && nums[mid] > nums[mid - 1] && nums[mid] > nums[mid + 1]){return mid;}if(nums[mid] > nums[mid + 1]){r = mid - 1;}else{l = mid + 1;}}return l;}
}// 之前参考题解的代码:
class Solution {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;while(left < right){int mid = (left + right) / 2;if(nums[mid] > nums[mid + 1]){right = mid;}else{left = mid + 1;}}return left;}
}相关文章:

LC:二分查找——杂记
文章目录 268. 丢失的数字162. 寻找峰值 268. 丢失的数字 LC将此题归类为二分查找,并且为简单题,下面记一下自己对这道题目的思考。 题目链接:268.丢失的数字 第一次看到这个题目,虽然标注的为简单,但肯定不能直接排…...

GA/T1400视图库平台EasyCVR多品牌摄像机视频平台前端监控摄像头镜头的基础知识
在现代安全监控系统中,摄像机镜头作为捕捉图像的关键组件,其选择和应用直接影响到监控图像的质量和系统的整体性能。随着技术的发展,摄像机镜头的种类和功能也在不断扩展,以适应各种复杂的监控环境和需求。对于相机成像来讲&#…...

【C++】踏上C++的学习之旅(六):深入“类和对象“世界,掌握编程的黄金法则(一)
文章目录 前言1. "面向过程"和"面向对象"的碰撞1.1 面向过程1.2 面向对象 2. "类"的引入3. "类"的定义3.1 🍉语法展示:3.2 "类"的两种定义方式3.3 "类"的命名规则 4. 类的访问限定符以及封…...

【物联网技术】ESP8266 WIFI模块在STA模式下作为TCP客户端上电自动进入透传数据模式
前言:讲解如何在ESP8266 WIFI模块在STA模式下作为TCP客户端与网络调试助手(TCP服务器)上电自动进入透传数据模式,而不需重新再发指令配置进入透传模式。 演示视频: ESP8266 WIFI模块在STA模式下作为TCP客户端上电自动进入透传数据模式 wifi模块在STA模式下作为TCP客户端相…...

重构代码之用委托替代继承
在代码重构中,用委托替代继承 是一种用于改善代码设计和提高灵活性的重要技术。它的核心思想是,将子类与父类的直接继承关系转换为委托关系,即子类不再直接继承父类,而是通过持有父类的实例来访问所需的功能。 一、为什么需要用委…...

软件设计师下午题UML15分
一、涉及到的图及对应关系 二、例题 1.用例图和类图的例题 解析及答案 2.状态图和类图的例题 3.通信图和类图例题 例题...

css background-image背景图片轮播
1、CSS背景样式有以下几种: 背景颜色(background-color):设置元素的背景颜色。背景图片(background-image):设置元素的背景图片。背景重复(background-repeat)ÿ…...

java---认识异常(详解)
还有大家来到权权的博客~欢迎大家对我的博客提出意见哦,有错误会及时改进的~点击进入我的博客主页 目录 一、异常的概念及体系结构1.1 异常的概念1.2 异常的体系结构1.3异常的分类 二、异常的处理2.1防御式编程2.2 异常的抛出2.3 异常的捕获2.3.1异常声明throws2.3.…...

Linux基础学习笔记
Linux基础学习笔记 Linux目录结构: 具体的目录结构: /bin [重点] (/usr/bin 、 /usr/local/bin) • 是Binary的缩写, 这个目录存放着最经常使用的命令 /home [重点] • 存放普通用户的主目录,在Linux中每个用户都有一个自己的目录,一…...
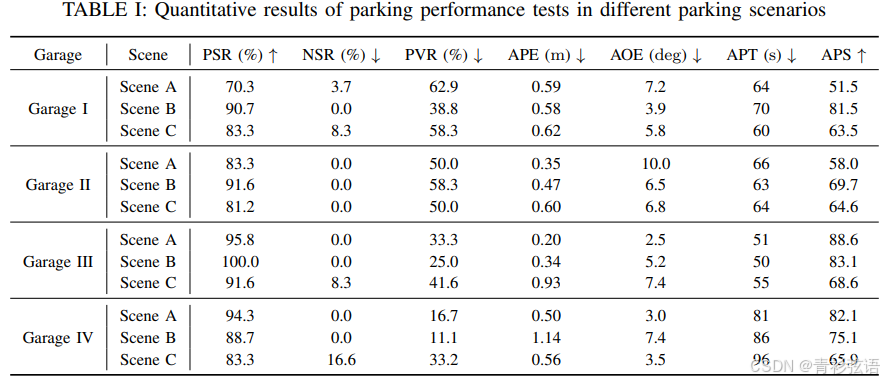
自动泊车端到端算法 ParkingE2E 介绍
01 算法介绍 自主泊车是智能驾驶领域中的一项关键任务。传统的泊车算法通常使用基于规则的方案来实现。因为算法设计复杂,这些方法在复杂泊车场景中的有效性较低。 相比之下,基于神经网络的方法往往比基于规则的方法更加直观和多功能。通过收集大量专家…...
《手写Spring渐进式源码实践》实践笔记(第十七章 数据类型转换)
文章目录 第十七章 数据类型转换工厂设计实现背景技术背景Spring数据转换实现方式类型转换器(Converter)接口设计实现 业务背景 目标设计实现代码结构类图实现步骤 测试事先准备属性配置文件转换器工厂Bean测试用例测试结果: 总结 第十七章 数…...

W3C HTML 活动
关于W3C(万维网联盟)的HTML活动,我们可以从HTML的不同版本的发展历程中了解其主要的活跃时期和贡献。 HTML 2.0:这个版本的HTML是由Internet工程工作小组(IETF)的HTML工作组于1996年开发的。它是HTML的早期…...

机器学习—为什么我们需要激活函数
如果我们使用神经网络中每个神经元的线性激活函数,回想一下这个需求预测示例,如果对所有节点使用线性激活函数,在这个神经网络中,事实证明,这个大神经网络将变得与线性回归没有什么不同,所以这将挫败使用神…...

软考系统架构设计师论文:论软件的可靠性评价
试题四 论软件的可靠性评价 软件可靠性评价是软件可靠性活动的重要组成部分,既适用于软件开发过程,也可针对最 终软件系统。在软件开发过程中使用软件可靠性评价,可以使用软件可靠性模型,估计软件当前的可靠性,以确认是否可以终止测试并发布软件,同时还可以预计软件要达…...
的创建、调用及销毁)
C++:线程(thread)的创建、调用及销毁
在 C 中,线程的管理主要依赖于标准库 std::thread,自 C11 起,这一功能被标准化,使得我们能够更加方便地创建、管理和销毁线程。这里我们详细讲解线程的创建、调用和销毁流程。 1. 线程的创建 创建线程通常是为了在单独的线程中执…...

关于随身wifi,看了再决定要不要买!2024年最受欢迎的随身wifi品牌推荐!
话费、流量费缴纳起来肉疼,毕竟不是每个月都有很大需求,主打一个该省省该花花。特别是短租人群、在校学生、出差或旅游的人群、追求高性价比的人群,随身Wifi特别实用,出门当WiFi,在家当宽带,两不耽误&#…...

SpringMVC总结 我的学习笔记
SpringMVC总结 我的学习笔记 一、SpringMVC简介1.MVC2.SpringMVC概述3. SpringMVC中的核心组件4.SpringMVC核心架构流程 二、SpringMVC框架实例具体实现使用注解实现 四、数据处理及跳转1.结果跳转方式2.处理器方法的参数与返回值处理提交数据数据显示到前端 五、RestFul风格1.…...

DevCheck Pro手机硬件检测工具v5.33
前言 DevCheck Pro是一款手机硬件和操作系统信息检测查看工具,该软件的功能非常强大,为用户提供了系统、硬件、应用程序、相机、网络、电池等一系列信息查看功能 安装环境 [名称]:DevCheckPro [版本]:5.33 [大小]&a…...

数据分析ReAct工作流
让我用一个数据分析项目的例子来展示plan-and-execute框架的应用。这个例子会涉及数据处理、分析和可视化等任务。 from typing import List, Dict, Any from dataclasses import dataclass import json from enum import Enum import logging from datetime import datetime#…...

Rust-AOP编程实战
文章本天成,妙手偶得之。粹然无疵瑕,岂复须人为?君看古彝器,巧拙两无施。汉最近先秦,固已殊淳漓。胡部何为者,豪竹杂哀丝。后夔不复作,千载谁与期? ——《文章》宋陆游 【哲理】文章…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
