[ABC239E] Subtree K-th Max
[ABC239E] Subtree K-th Max
题面翻译
给定一棵 n n n 个节点的树,每个节点的权值为 x i x_i xi。
现有 Q Q Q 个询问,每个询问给定 v , k v,k v,k,求节点 v v v 的子树第 k k k 大的数。
0 ≤ x i ≤ 1 0 9 , 2 ≤ n ≤ 1 0 5 , 1 ≤ Q ≤ 1 0 5 , 1 ≤ k ≤ 20 0\le x_i\le10^9,2\le n\le10^5,1\le Q\le10^5,1\le k\le20 0≤xi≤109,2≤n≤105,1≤Q≤105,1≤k≤20。
翻译提供:xiaohaoaibiancheng66
题目描述
$ N $ 頂点の根付き木があります。頂点には $ 1 $ から $ N $ の番号がついており、根は頂点 $ 1 $ です。
$ i $ 番目の辺は頂点 $ A_i $ と $ B_i $ を結んでいます。
頂点 $ i $ には整数 $ X_i $ が書かれています。
$ Q $ 個のクエリが与えられます。$ i $ 番目のクエリでは整数の組 $ (V_i,K_i) $ が与えられるので、次の問題に答えてください。
- 問題:頂点 $ V_i $ の部分木に含まれる頂点に書かれた整数のうち、大きい方から $ K_i $ 番目の値を求めよ
输入格式
入力は以下の形式で標準入力から与えられる。
$ N $ $ Q $ $ X_1 $ $ \ldots $ $ X_N $ $ A_1 $ $ B_1 $ $ \vdots $ $ A_{N-1} $ $ B_{N-1} $ $ V_1 $ $ K_1 $ $ \vdots $ $ V_Q $ $ K_Q $
输出格式
$ Q $ 行出力せよ。$ i $ 行目には $ i $ 番目のクエリに対する答えを出力せよ。
样例 #1
样例输入 #1
5 2
1 2 3 4 5
1 4
2 1
2 5
3 2
1 2
2 1
样例输出 #1
4
5
样例 #2
样例输入 #2
6 2
10 10 10 9 8 8
1 4
2 1
2 5
3 2
6 4
1 4
2 2
样例输出 #2
9
10
样例 #3
样例输入 #3
4 4
1 10 100 1000
1 2
2 3
3 4
1 4
2 3
3 2
4 1
样例输出 #3
1
10
100
1000
提示
制約
- $ 2\ \leq\ N\ \leq\ 10^5 $
- $ 0\leq\ X_i\leq\ 10^9 $
- $ 1\leq\ A_i,B_i\leq\ N $
- $ 1\leq\ Q\ \leq\ 10^5 $
- $ 1\leq\ V_i\leq\ N $
- $ 1\leq\ K_i\leq\ 20 $
- 与えられるグラフは木である
- 頂点 $ V_i $ の部分木は頂点を $ K_i $ 個以上持つ
- 入力に含まれる値は全て整数である
Sample Explanation 1
この入力において与えられる木は下図のようなものです。  $ 1 $ 番目のクエリでは、頂点 $ 1 $ の部分木に含まれる頂点 $ 1,2,3,4,5 $ に書かれた数のうち大きい方から $ 2 $ 番目である $ 4 $ を出力します。 $ 2 $ 番目のクエリでは、頂点 $ 2 $ の部分木に含まれる頂点 $ 2,3,5 $ に書かれた数のうち大きい方から $ 1 $ 番目である $ 5 $ を出力します。
思路:刚看到这种题,就感觉写起来很别扭怎么,还是要敢写才行,错了不要紧,根据k的范围我们可以知道我们只需要暴力遍历即可得出来每一个节点前20大的数
#include<bits/stdc++.h>using namespace std;typedef long long ll;
typedef pair<ll, ll>PII;
const int N = 2e5 + 10;
const int MOD = 998244353;
const int INF = 0X3F3F3F3F;
const int dx[] = {-1, 1, 0, 0, -1, -1, +1, +1};
const int dy[] = {0, 0, -1, 1, -1, +1, -1, +1};
const int M = 1e6 + 10;vector<ll>ans[N], a(N + 1), ed[N];//存树void dfs(int u, int fa)
{vector<ll>o;o.push_back(a[u]);//存上自己for(auto it : ed[u]){if(it == fa) continue;dfs(it, u);//一直遍历it那一个节点for(auto k : ans[it])//相当于那个节点上的数都给遍历完了{o.push_back(k);}}sort(o.begin(), o.end(), greater<ll>());//排好序//我们只需要取出前20即可int si = min(20, (int)o.size());for(int i = 0; i < si; i ++){ans[u].push_back(o[i]);}
}
int main()
{int n, q;cin >> n >> q;for(int i = 1; i <= n; i ++){cin >> a[i];}for(int i = 1; i <= n - 1; i ++){int u, v;cin >> u >> v;ed[u].push_back(v);ed[v].push_back(u);//存图}dfs(1, -1);//预处理出来第k大while(q --){int u, k;cin >> u >> k;cout << ans[u][k - 1] << endl;//因为下标从0开始的}
}
相关文章:

[ABC239E] Subtree K-th Max
[ABC239E] Subtree K-th Max 题面翻译 给定一棵 n n n 个节点的树,每个节点的权值为 x i x_i xi。 现有 Q Q Q 个询问,每个询问给定 v , k v,k v,k,求节点 v v v 的子树第 k k k 大的数。 0 ≤ x i ≤ 1 0 9 , 2 ≤ n ≤ 1 0 5 , …...
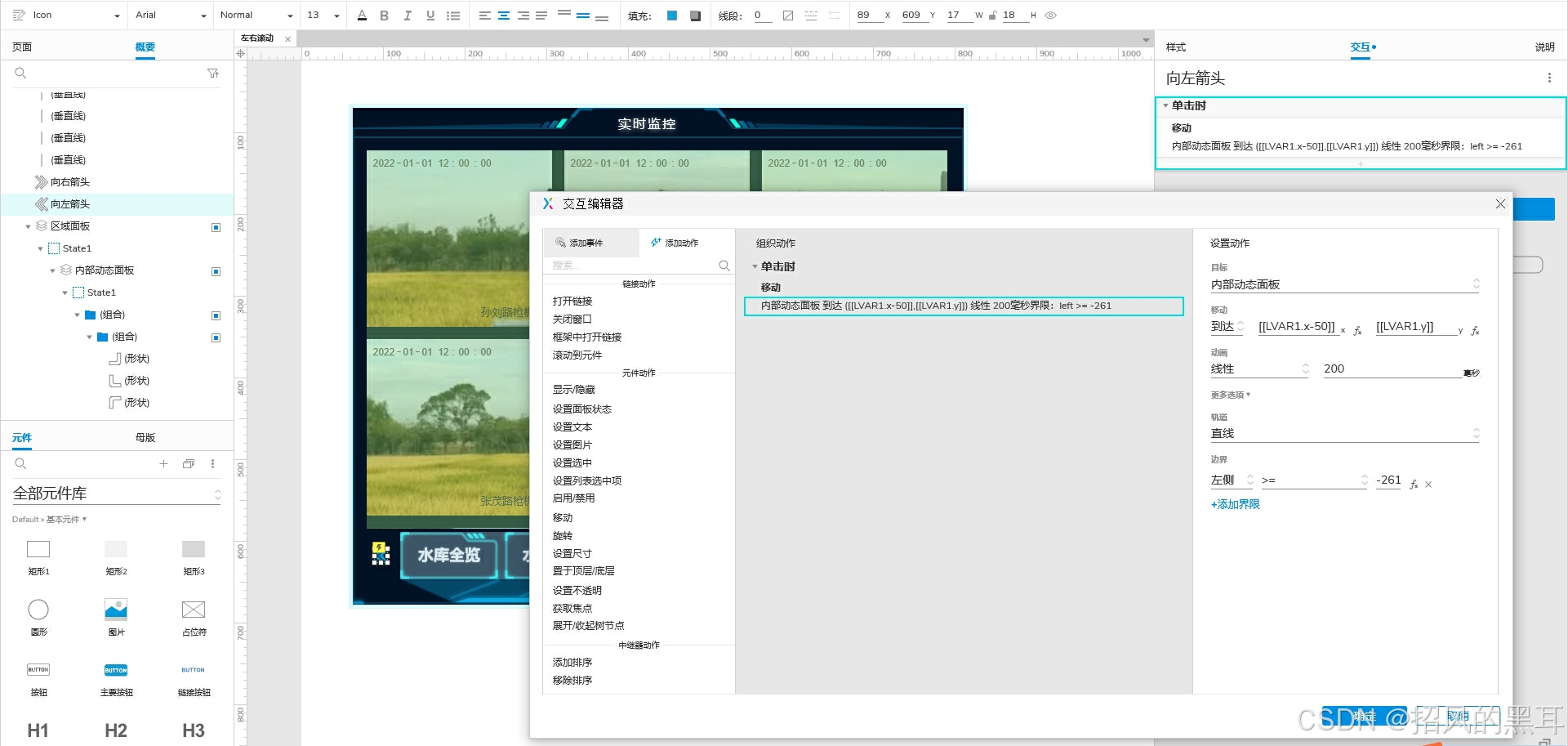
Axure设计之左右滚动组件教程(动态面板)
很多项目产品设计经常会遇到左右滚动的导航、图片展示、内容区域等,接下来我们用Axure来实现一下左右滚动的菜单导航。通过案例我们可以举一反三进行其他方式的滚动组件设计,如常见的上下滚动、翻页滚动等等。 一、效果展示: 1、点击“向左箭…...

善用Git LFS来降低模型文件对磁盘的占用
将讲一个实际的例子:对于模型文件,动辄就是好几个G,而有的仓库更是高达几十G,拉一个仓库到本地,稍不注意直接磁盘拉满都有可能。 比如:meta-llama-3.1-8b-instruct,拉到本地后发现居然占用了60G…...

Oracle RAC的thread
参考文档: Real Application Clusters Administration and Deployment Guide 3 Administering Database Instances and Cluster Databases Initialization Parameter Use in Oracle RAC Table 3-3 Initialization Parameters Specific to Oracle RAC THREAD Sp…...

如何创建备份设备以简化 SQL Server 备份过程?
SQL Server 中的备份设备是什么? 在 SQL Server 中,备份设备是用于存储备份数据的物理或逻辑介质。备份设备可以是文件、设备或其他存储介质。主要类型包括: 文件备份设备:通常是本地文件系统中的一个或多个文件。可以是 .bak 文…...

DeBiFormer实战:使用DeBiFormer实现图像分类任务(一)
摘要 一、论文介绍 研究背景:视觉Transformer在计算机视觉领域展现出巨大潜力,能够捕获长距离依赖关系,具有高并行性,有利于大型模型的训练和推理。现有问题:尽管大量研究设计了高效的注意力模式,但查询并…...

【go从零单排】迭代器(Iterators)
🌈Don’t worry , just coding! 内耗与overthinking只会削弱你的精力,虚度你的光阴,每天迈出一小步,回头时发现已经走了很远。 📗概念 在 Go 语言中,迭代器的实现通常不是通过语言内置的迭代器类型&#x…...

Java与HTML:构建静态网页
在Web开发领域,HTML是构建网页的基础标记语言,而Java作为一种强大的编程语言,也能够在创建HTML内容方面发挥重要作用。今天,我们就来探讨一下如何使用Java来制作一个不那么简单的静态网页。 一、项目准备 首先,我们需…...

软件测试:测试用例详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 一、通用测试用例八要素 1、用例编号; 2、测试项目; 3、测试标题; 4、重要级别; 5、预置…...

FreeSWITCH Ubuntu 18.04 源码编译
应朋友邀请,试了试 FreeSWITCH Ubuntu 18.04 源码编译,交的作业如下: #!/bin/bash####### Ubuntu 18.04 LTS ####### ARM64 ####### FreeSWITCH 1.10.12apt update && \ apt install -y --fix-missing git sed bison build-essentia…...

spring—boot(整合redis)
整合redis 第一步导入数据源 <!--redis--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency> RedisConfig(默认有RedisTemplate&#…...

Python 包镜像源
阿里云、清华大学和豆瓣之外,还有许多其他的 Python 包镜像源。下面是更新后的代码,增加了更多常用的镜像源,如华为云、腾讯云等 import tkinter as tk from tkinter import messagebox import os# 定义 pip 配置文件路径 pip_config_file …...

Sigrity SPEED2000 Power Ground Noise Simulation模式如何进行电源阻抗仿真分析操作指导(一)-无电容
Sigrity SPEED2000 Power Ground Noise Simulation模式如何进行电源阻抗仿真分析操作指导(一)-无电容 Sigrity Power Ground Noise Simulation模式同样可以用来观测电源网络的自阻抗,以下图为例进行说明 2D 视图 3D view 本例要观测的是U17端口处的自阻抗࿰…...

Unity3D ASTC贴图压缩格式详解
一、技术详解 ASTC(Adaptive Scalable Texture Compression)是一种先进的纹理压缩格式,特别适用于OpenGL ES 3.0及更高版本。ASTC在2012年推出,自那以后已经成为游戏开发中重要的纹理压缩技术。它不仅在iOS设备上得到广泛应用&am…...

Docker的轻量级可视化工具Portainer
docker目录 1 Portainer官方链接2 是什么?3 下载安装4 跑通一次5 后记 1 Portainer官方链接 这里给出portainer的官方链接:https://www.portainer.io/ portainer安装的官方链接:https://docs.portainer.io/start/install-ce/server/docker/l…...

udp丢包问题
udp或者tcp丢包问题监测方式: netstat -su 问题分析: 1. 内存 2. cpu 3. 发送接收缓存 动画图解 socket 缓冲区的那些事儿-CSDN博客...
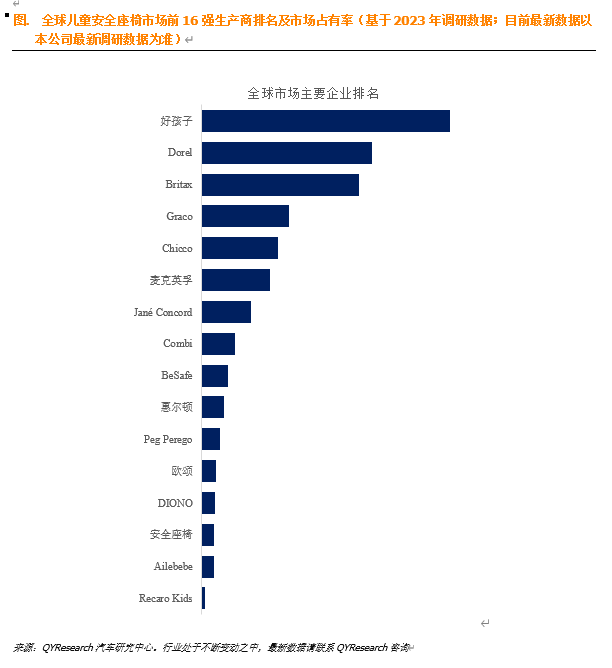
儿童安全座椅行业全面深入分析
儿童安全座椅就是一种专为不同体重(或年龄段)的儿童设计,将孩子束缚在安全座椅内,能有效提高儿童乘车安全的座椅。欧洲强制性执行标准ECE R44/03的定义是:能够固定到机动车辆上,带有ISOFIX接口、LATCH接口的…...

【笔记】扩散模型(九):Imagen 理论与实现
论文链接:Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding 非官方实现:lucidrains/imagen-pytorch Imagen 是 Google Research 的文生图工作,这个工作并没有沿用 Stable Diffusion 的架构,而是级…...

05 SQL炼金术:深入探索与实战优化
文章目录 SQL炼金术:深入探索与实战优化一、SQL解析与执行计划1.1 获取执行计划1.2 解读执行计划 二、统计信息与执行上下文2.1 收集统计信息2.2 执行上下文 三、SQL优化工具与实战3.1 SQL Profile3.2 Hint3.3 Plan Baselines3.4 实战优化示例 SQL炼金术:…...

Linux用lvm格式挂载磁盘
Linux用lvm格式挂载磁盘 本次目标是将磁盘/dev/sdd以lvm格式挂载到/backup目录作为备份盘来用 1、查看当前磁盘 [rootquentin ~]# lsblk NAME MAJ:MIN RM SIZE RO TYPE MOUNTPOINT sda 8:0 0 300G 0 disk ├─sda1 8:1 0 1G…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
