vue3的自定义hooks怎么写?
写个hook函数去追踪鼠标位置:
没用hook前:
<script setup>
import { ref, onMounted, onUnmounted } from 'vue'const x = ref(0)
const y = ref(0)function update(event) {x.value = event.pageXy.value = event.pageY
}onMounted(() => window.addEventListener('mousemove', update))
onUnmounted(() => window.removeEventListener('mousemove', update))
</script><template>Mouse position is at: {{ x }}, {{ y }}</template>用hook后:
//主页面:<template>Mouse position is at: {{ x }}, {{ y }}</template><script setup>
import { useMouse } from './mouse.js'const { x, y } = useMouse()
</script>在同一目录下新建mouse.js文件,在文件内写入以下内容:
// mouse.js
import { ref, onMounted, onUnmounted } from 'vue'// 按照惯例,组合式函数名以“use”开头
export function useMouse() {// 被组合式函数封装和管理的状态const x = ref(0)const y = ref(0)// 组合式函数可以随时更改其状态。function update(event) {x.value = event.pageXy.value = event.pageY}// 一个组合式函数也可以挂靠在所属组件的生命周期上// 来启动和卸载副作用onMounted(() => window.addEventListener('mousemove', update))onUnmounted(() => window.removeEventListener('mousemove', update))// 通过返回值暴露所管理的状态return { x, y }
}相关文章:

vue3的自定义hooks怎么写?
写个hook函数去追踪鼠标位置: 没用hook前: <script setup> import { ref, onMounted, onUnmounted } from vueconst x ref(0) const y ref(0)function update(event) {x.value event.pageXy.value event.pageY }onMounted(() > window.ad…...

SpringBoot项目编译报错 类文件具有错误的版本 61.0, 应为 52.0
springboot项目在编译时报错: /Users/Apple/Developer/art/caicai/cai-api/dubbo-samples/1-basic/dubbo-samples-spring-boot/dubbo-samples-spring-boot-provider/src/main/java/org/apache/dubbo/springboot/demo/provider/ProviderApplication.java:22:32 java…...

【网络】应用层——HTTP协议
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:了解什么是HTTP协议。 > 毒鸡汤:有些事情,总是不明白,所以我不会坚持。早安! > 专栏选自:网络 &g…...

ServletContext介绍
文章目录 1、ServletContext对象介绍1_方法介绍2_用例分析 2、ServletContainerInitializer1_整体结构2_工作原理3_使用案例 3、Spring案例源码分析1_注册DispatcherServlet2_注册配置类3_SpringServletContainerInitializer 4_总结 ServletContext 表示上下文对象,…...
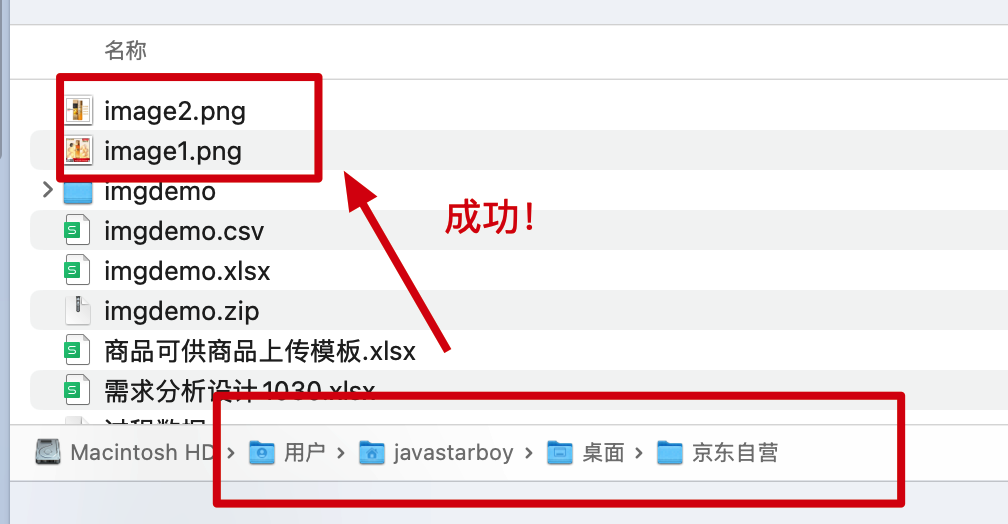
让AI帮我用java实现EasyExel读取图片—支持WPS嵌入图片
🌈 场景概述 java 小伙伴相信都使用 EasyExcel 以及 POI 库实现过 Excel 批量导入、导出功能,但只有部分人实现过 excel 导入带图片数据的场景。这个技术实现手段网上也有很多案例和demo,最常见的就是通过 XSSFPictureData 来实现。但是在 W…...

C# 实现对指定句柄的窗口进行键盘输入的实现
在C#中实现对指定句柄的窗口进行键盘操作,可以通过多种方式来实现。以下是一篇详细的指南,介绍如何在C#中实现这一功能。 1. 使用Windows API函数 在C#中,我们可以通过P/Invoke调用Windows API来实现对指定窗口的键盘操作。以下是一些关键的…...

深度学习之卷积问题
1 卷积在图像中有什么直观作用 在卷积神经网络中,卷积常用来提取图像的特征,但不同层次的卷积操作提取到的特征类型是不相同的,特征类型粗分如表1所示。 表1 卷积提取的特征类型 卷积层次特征类型浅层卷积边缘特征中层卷积局部特征深…...

yum安装zabbix5.0升级php到74的办法
【背景】 公司时不时有扫描漏洞,之前发现了php漏洞,因开启防火墙,限定IP+端口,暂时躲过升级;现在,老话重提,开启了KPI考核,躲是躲不过去的了,升级吧 【难题】 服务器为centos7,因操作系统问题,只能安装zabbix5.0。当时图省力,官网的办法,都是yum安装,很是简便。…...
JavaWeb合集23-文件上传
二十三 、 文件上传 实现效果:用户点击上传按钮、选择上传的头像,确定自动上传,将上传的文件保存到指定的目录中,并重新命名,生成访问链接,返回给前端进行回显。 1、前端实现 vue3AntDesignVue实现 <tem…...

当AI遇上时尚:未来的衣橱会由机器人来打理吗?
内容概要 在当今这个快速发展的时代,人工智能与时尚的结合正在逐渐改写我们对衣橱管理的认知。传统的衣橱管理常常面临着空间不足、穿搭单调及库存过多等挑战,许多人在挑选服饰时难以做出决策。然而,随着技术的进步,智能推荐和自…...

【初阶数据结构篇】二叉树OJ题
文章目录 须知 💬 欢迎讨论:如果你在学习过程中有任何问题或想法,欢迎在评论区留言,我们一起交流学习。你的支持是我继续创作的动力! 👍 点赞、收藏与分享:觉得这篇文章对你有帮助吗࿱…...

Windows系统中Oracle VM VirtualBox的安装
一.背景 公司安排了师带徒,环境搭建问题一直是初级程序员头疼的事情,我记录一下这些基础的内容,方便初学者。大部分开发者的机器还是windows系统,所以写了怎么安装。 二.版本信息及 操作系统:windows11 家庭版…...
)
go语言使用总结(持续更新)
整理后的内容如下: 1. 先了解函数签名,再了解传入参数以及调用 函数签名是函数的声明部分,包括函数名、参数列表和返回值列表。理解函数签名是理解函数行为的第一步,尤其是在了解参数类型、参数数量和返回值类型等方面。通过了解…...

如何在Android中自定义property
在Android中创建自定义的属性(Android property)通常用于调试、性能调优或传递应用和系统之间的信息。 以下是如何在Android中创建和使用自定义属性的步骤: 1. 定义属性 在Android中,属性是以“属性名称属性值”形式定义的键值对…...
机器学习5_支持向量机_原问题和对偶问题——MOOC
目录 原问题与对偶问题的定义 定义该原问题的对偶问题如下 在定义了函数 的基础上,对偶问题如下: 综合原问题和对偶问题的定义得到: 定理一 对偶差距(Duality Gap) 强对偶定理(Strong Duality Theo…...

索引的细节
目录 什么是线性 搜索算法? 算法:二进制搜索算法 二进制搜索如何工作? 什么是二叉排序树? 构建二叉排序树 什么是AVL树? AVL树的性能分析 什么是线性 搜索算法? 线性搜索是一种非常简单的搜索算法。在…...

LeetCode 540.有序数组中的单一元素
思路一:hash,键存入元素,值存入次数,然后遍历,不是最优解 思路二:二分查找 假设数组为 [1, 1, 2, 2, 3, 4, 4],其中唯一出现一次的元素是 3。在一个有序数组中,如果没有唯一的元素&…...

【图文】【DIY便签】如何自行编译OPENCV使用动态库
1 去官网下载安装包和源码 下面红色圈中的是源码,绿色圈中的是安装包: 2 配置工具链 安装过程不说了,教程到处都是。编译的话使用CMAKE,配置如下: 上面两个路径分别是: 源码目录编译生成的文件放置的位…...

WordPress文章自动提交Bing搜索引擎:PHP推送脚本教程
随着网站SEO优化的重要性日益增加,将新发布的内容快速提交到搜索引擎显得尤为重要。尤其对于Bing站长平台,自动化推送能让Bing尽快发现和索引我们网站的新内容。本文将详细介绍如何通过PHP脚本自动推送WordPress当天发布的文章至Bing站长平台,确保新文章被Bing及时收录。 前…...

C++题目分享
嗨嗨嗨,我又来更新这个系列了,很久没更新了。让我们看一看有那些有趣的题目: 题目一: 1.以单链表作为存储结构,实现线性表的就地逆置(提示,就地逆置:在不使用额外的数据结构或空间…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
