简易入手《SOM神经网络》的本质与原理
原创文章,转载请说明来自《老饼讲解神经网络》:www.bbbdata.com
关于《老饼讲解神经网络》:
本网结构化讲解神经网络的知识,原理和代码。
重现matlab神经网络工具箱的算法,是学习神经网络的好助手。
目录
一、入门原理解说
01. 基于Kohonen规则的聚类算法
02. SOM聚类的思想
03. SOM神经网络的拓扑图
04. SOM的模型表达式
编后语
二、SOM-代码重写(单样本训练)
01. 代码结构说明
02. 代码运行结果解说
03. 具体代码
SOM神经网络(Self-organizing Feature Map)是Kohonen在1981年提出的一种用于聚类的神经网络,是神经网络家族中经典、重要且广泛应用的一员。
本篇第一节先聚焦于讲清SOM是个什么东西,解决什么问题,思路是什么,有什么特性,
第二节则扒取matlab的源码,自写《SOM-单样本训练算法》,即用自己的代码逻辑重现matlab工具箱的效果。
笔者语
SOM不是一个困难的算法,但要讲清SOM,却是一个困难的问题。
笔者曾想一张文章讲完SOM,左揉右捏,后来发现,这鬼东西,越图快越不行。
为什么SOM必须慢慢讲述,主要是因为SOM的思想经历了三阶段:
Kohonen规则 --> 单样本训练 --> 批量样本训练
想直接讲述批量样本训练根本讲不了。
谨此,希望读者也不要图快,一步一步来。
一、入门原理解说
01. 基于Kohonen规则的聚类算法
聚类问题
口语描述:假设数据是一团团的,我们希望找出这些一团团数据的中心点(聚类中心),样本离哪个聚类中心最近,就将样本判为该聚类中心。
基于Kohonen规则的聚类方法
kohonen规则聚类很简单,
先随机初始化k个聚类中心点,
然后每次选出一个样本,将离它最近的聚类点往它移动,使该聚类点更靠近它,如此反复m次。
更新法则如下:

其中,
:离样本最近的聚类中心点。
: 学习率。
kohonen规则的有效性
kohonen规则虽然简单,然而它却是行之有效的。
且看一个Demo:
平面中有四簇数据,
我们先随机初始化5个聚类中心点,
然后使用Kohonen规则调整聚类中心点的位置,
可以看到,经过一定步数后,聚类中心点移到了四类数据的中心位置附近。
Demo代码:
% Kohonen聚类规则
rand('seed',70);
%------------生成样本数据-------------
dataC = [2.5,2.5;7.5,2.5;2.5,7.5;7.5,7.5]; % 生成四个样本中心
sn = 40; % 样本个数
X = rand(sn,2)+dataC(mod(1:sn,4)+1,:); % 随机生成样本点% -----------初始化聚类中心点--------------
kn = 5; % 聚类中心点个数
C = rand(kn,2)*10; % 随机生成聚类中心
C0 = C; % 备份聚类中心点的初始值% -----------使用样本训练聚类中心点-----------
lr = 0.1; % 学习率
for t = 1:50for i = 1:sncur_x = X(i,:); % 提取一个样本dist = sum((repmat(cur_x,kn,1) - C).^2,2); % 计算样本到各个聚类中心点的距离[~,idx] = min(dist); % 找出最近的聚类中心点C(idx,:) = C(idx,:) + lr*(cur_x - C(idx,:)); % 将该聚类中心点往样本靠近end
end% ----------画图------------------------
subplot(1,2,1)
plot(X(:,1),X(:,2),'*');
hold on
plot(C0(:,1),C0(:,2),'or','MarkerFaceColor','g');subplot(1,2,2)
plot(X(:,1),X(:,2),'*');
hold on
plot(C(:,1),C(:,2),'or','MarkerFaceColor','g');
02. SOM聚类的思想
SOM是Kohonen规则的改进,
它在更新离样本最近的聚类中心点P的的时候,会把P的邻近聚类中心点也一起更新。
请注意,初学者很容易误会,以为SOM所指的邻近聚类点就是目标聚类点附近的聚类点,其实不是,SOM对“邻近聚类点”有自己的定义。
SOM聚类点的距离与邻近聚类点
SOM是先引入一个拓扑结构,把所有聚类点连结在一起,然后籍此来定义距离。
拓扑结构
拓扑结构可以是一维的,二维的,三维的,等等,最常用是二维
例如最常用的二维六边形拓扑结构:
距离的定义
在SOM中,两点之间的距离,
是指在引入的拓扑结构中,这两点之间的最小边数。
邻近聚类点
点P的邻近聚类点是指与P的最小连结边数小于某个阈值的聚类点。
例如,
当邻域距离阈值为1时,点P的邻近聚类点,是与点P直接连接的点。
当邻域距离阈值为2时,则是到达点P不超过2条边的聚类点。
当邻域距离阈值为k时,就是指经过m(m<=k)条边可达点P的聚类点。
SOM的更新方法
SOM更新的方法与上面所说的Kohonen规则思想是一样的,
不同点在于,SOM在更新离样本最近的聚类中心点P的的时候,会把P的邻近聚类中心点也一起更新
更细节的,有以下三点:
1、更新邻近聚类点:
更新样本最近点P的同时,P的邻近聚类点也一起更新,(P的学习率要比邻近聚类点更大一些)。
2、增加学习率的收缩机制:
随着更新步数,学习率越来越小。
3、邻近距离收缩机制:
随着更新步数,邻近距离阈值越来越小,渐渐的,只有目标点及其邻边聚类点。
比起纯粹的Kohonen规则,虽然改动不大,在代码编写上,却要复杂很多。
复杂是因为要初始化拓扑结构,获得点与点之间的距离矩阵(这里说的距离是上面所说的边数),以便在更新时获取邻近聚类点。
说 明
● 以上的更新方法来自matlab老版本的单样本训练算法(learnsom)。
● matlab新版本已采用了批量更新算法(learnsomb)。
两种方法的细节,我们都另起文章细讲,并扒出源码,重现matlab的实现逻辑。
03. SOM神经网络的拓扑图
网络拓扑图
SOM神经网络是典型的三层神经网络,
拓扑图如下:
第一层是输入层
第二层是隐层,
隐层有多少个隐节点,就代表有多少个聚类中心点 ( 聚类中心点的位置就是该隐节点与输入的连接权重 ) 。
第三层是输出层
输出层是one-hot格式(即[0 0 0 1]这样的格式),
它的节点与隐层节点个数一致,
它的值由隐层节点竞争得到, 即隐层节点哪个值最大,对应的输出节点就为1,其余为0。
带隐层拓扑的网络拓扑图
往往还会把隐层节点之间的拓扑结构一起画上,
则SOM的网络拓扑图会如下:
PASS:输出节点之间的拓扑结构对于最终模型的应用上是没有任何影响的,它只是在训练过程中需要使用。
04. SOM的模型表达式
SOM的模型数学表达式为:
其中,
● dist 为x和W的欧氏距离
例如,2输出3隐节点时,,

则:

● compet 为竞争函数,
它将向量最大的值置为1,其实置0
例如,compet([ 2 5 3 ]) = [ 0 1 0 ]
SOM模型输出的计算,简单来说,就是x离W哪行最近,就为1,其余为0.
背后意义就是离哪个聚类中心点近,就判为哪个聚类点。
编后语
本文我们先大概摸清SOM神经网络是什么,
它的思路其实并不复杂,只是Kohonen的基础上,在隐节点引入了一个拓扑结构来定义邻域
由于我们往往看到的基本都是带隐节点拓扑结构的网络拓扑图,很容易产生误会,以为隐层节点间相互连接,
其实隐节点的拓扑图只在训练阶段用于获取邻域节点,与最终的模型并没有任何关系。
在接下来的文章,我们把SOM的代码按matlab内部逻辑实现后,我们将更清晰SOM算法的具体细节与算法流程。
二、SOM-代码重写(单样本训练)
本文是笔者细扒matlab2009b神经网络工具箱newsom的源码,
在源码的基础上去除冗余代码,重现的简版newsom代码,代码与newsom的结果完全一致。
通过本代码的学习,可以完全细节的了解SOM单样本训练的实现逻辑。
01. 代码结构说明
代码主要包含了三个函数: testSomNet trainSomNet predictSomNet
testSomNet: 测试用例主函数,直接运行时就是执行该函数。
1、数据生成:随机生成一组训练数据,
2、用自写的函数训练一个SOM网络,与预测结果。
3、使用工具箱训练一个SOM网络。
4、比较自写函数与工具箱训练结果是否一致(权重、训练误差的比较)
trainSomNet:网络训练主函数,用于训练一个SOM神经网络。
单样本训练方式,训练一个SOM神经网络
predictSomNet:用训练好的网络进行预测。
传入需要预测的X,与网络的权重矩阵,即可得到预测结果。
02. 代码运行结果解说
运行代码后,得到预测结果与对比结果,如下:
从中可以看到,自写代码与工具箱的逻辑一致。
相关文章
《BP神经网络梯度推导》
《BP神经网络提取的数学表达式》
《一个BP的完整建模流程》
相关文章:

简易入手《SOM神经网络》的本质与原理
原创文章,转载请说明来自《老饼讲解神经网络》:www.bbbdata.com 关于《老饼讲解神经网络》: 本网结构化讲解神经网络的知识,原理和代码。 重现matlab神经网络工具箱的算法,是学习神经网络的好助手。 目录 一、入门原理解说 01.…...

21.assert断言
assert(断言)主要用于在程序运行过程中检查某个条件是否满足,如果不满足则会触发错误并终止程序执行,可以帮助程序员在开发阶段及时发现可能存在的逻辑错误等问题。 通过断言调试程序,abotr() has been called 就是断言…...

15分钟学 Go 第 46 天 : 监控与日志
第46天:监控与日志 学习目标 了解如何实现应用监控与日志管理,掌握相关工具和最佳实践。 内容结构 引言监控的概念与工具 监控的定义常见监控工具 日志管理的概念与工具 日志的重要性常见日志管理工具 实现监控与日志的最佳实践 监控指标日志格式 实战…...

BFS 算法专题(四):多源 BFS
目录 1. 01 矩阵 1.1 算法原理 1.2 算法代码 2. 飞地的数量 2.1 算法原理 2.2 算法代码 3. 地图中的最高点 3.1 算法原理 3.2 算法代码 4. 地图分析 4.1 算法原理 4.2 算法代码 1. 01 矩阵 . - 力扣(LeetCode) 1.1 算法原理 采用 BFS 正难…...
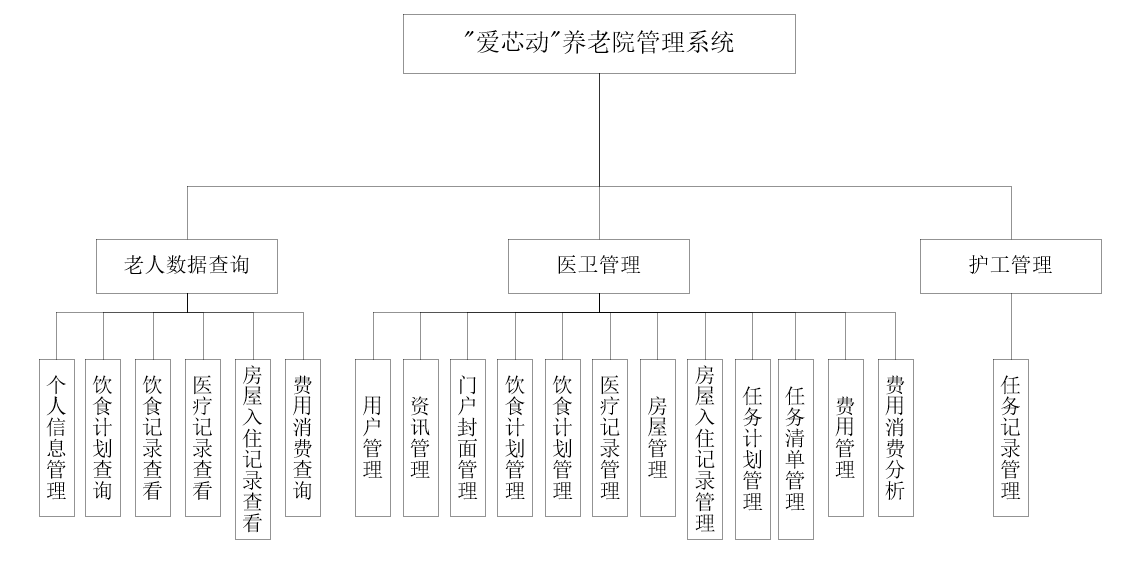
基于Spring Boot+Vue的养老院管理系统【原创】
一.系统开发工具与环境搭建 1.系统设计开发工具 后端使用Java编程语言的Spring boot框架 项目架构:B/S架构 运行环境:win10/win11、jdk17 前端: 技术:框架Vue.js;UI库:ElementUI; 开发工具&…...

Linux screen和cscope工具使用总结
1 minicom使用 1.1 minicom配置 第一次启动时: 如果输入sudo minicom提示错误,则需: sudo minicom -s 启动 出现配置菜单:选serial port setup 进入串口配置 输入A配置串口驱动为/dev/ttyUSB0 输入E配置速率为115200 8N1 输入F将 …...

深度学习面试八股汇总
按序发布: 深度学习——优化算法、激活函数、归一化、正则化 进入 深度学习——权重初始化、评估指标、梯度消失和梯度爆炸 进入 深度学习——前向传播与反向传播、神经网络(前馈神经网络与反馈神经网络)、常见算法 进入 深度学习——卷积神…...

微服务架构面试内容整理-API 网关-Gateway
Spring Cloud Gateway 是一个用于构建 API 网关的框架,它为微服务架构提供了灵活的路由和过滤功能。作为 Spring Cloud 生态的一部分,Gateway 提供了易于使用的 API 和强大的功能,适合用于现代微服务架构中的请求管理和服务交互。以下是 Spring Cloud Gateway 的主要特点、工…...

22.04Ubuntu---ROS2使用rclcpp编写节点C++
节点需要存在于功能包当中,功能包需要存在于工作空间当中。 所以我们要想创建节点,就要先创建一个工作空间,再创建功能包。 第一步:创建工作空间 mkdir -p chapt2_ws/src/ 第二步:创建example_cpp功能包,…...

XML 现实案例:深入解析与应用
XML 现实案例:深入解析与应用 XML(可扩展标记语言)自1998年成为W3C推荐标准以来,一直是数据交换和存储的重要工具。它是一种用于标记电子文件的结构化语言,使得数据不仅人类可读,而且机器可处理。本文将探讨XML在现实世界中的应用案例,展示其如何在不同领域中发挥作用。…...

Spring源码(十二):Spring MVC之Spring Boot
本篇将详细讨论Spring Boot 的启动/加载、处理请求的具体流程。我们先从一个简单的Spring Boot项目日志开始分析(这里假设读者已经仔细阅读完了前面的文章,且对Spring源码有一定深度的了解,否则会看得一脸懵逼)。 本文为2024重置…...

Kafka 之事务消息
前言: 在分布式消息系统中,事务消息也是一个热门课题,在项目的实际业务场景中,如果用到事务消息的场景也不少见,那 Kafka 作为一个高性能的分布式消息中间件,同样也支持事务消息,本篇我们将对 …...

小菜家教平台(四):基于SpringBoot+Vue打造一站式学习管理系统
前言 昨天配置完了过滤器,权限检验,基本的SpringSecurity功能已经配置的差不多了,今天继续开发,明天可能会暂停一天整理一下需求,然后就进行CRUD了。 今日进度 补充SpringSecurity异常处理和全局异常处理器 详细操作…...

解决 Vue3、Vite 和 TypeScript 开发环境下跨域的问题,实现前后端数据传递
引言 本文介绍如何在开发环境下解决 Vite 前端(端口 3000)和后端(端口 80)之间的跨域问题: 在开发环境中,前端使用的 Vite 端口与后端端口不一致,会产生跨域错误提示: Access to X…...

量化交易系统开发-实时行情自动化交易-3.3.数据采集流程
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来说说数据采集流程,后…...

探索PyAV:Python中的多媒体处理利器
文章目录 探索PyAV:Python中的多媒体处理利器第一部分:背景介绍第二部分:PyAV是什么?第三部分:如何安装PyAV?第四部分:简单的库函数使用方法1. 打开文件2. 查看流3. 遍历帧4. 编码帧5. 关闭输出…...

SpringBoot源码解析(三):启动开始阶段
SpringBoot源码系列文章 SpringBoot源码解析(一):SpringApplication构造方法 SpringBoot源码解析(二):引导上下文DefaultBootstrapContext SpringBoot源码解析(三):启动开始阶段 目录 前言一、入口二、SpringApplicationRunListener1、作用…...

C# const与readonly关键字的区别
在C#中,readonly关键字用于定义在对象创建后不能更改的字段。它可以与常量(const)有些相似,但也有显著不同。以下是readonly关键字的一些关键点: 定义与用法: readonly字段可以在类的构造函数中初始化,而const字段必须…...

【数据分享】1901-2023年我国省市县镇四级的逐年降水数据(免费获取/Shp/Excel格式)
之前我们分享过1901-2023年1km分辨率逐月降水栅格数据和Shp和Excel格式的省市县四级逐月降水数据,原始的逐月降水栅格数据来源于彭守璋学者在国家青藏高原科学数据中心平台上分享的数据!基于逐月数据我们采用求年累计值的方法得到逐年降水栅格数据&#…...
)
hhdb数据库介绍(9-4)
访问安全 权限体系 计算节点有两类用户,一类是计算节点数据库用户,用于操作数据,执行SELECT,UPDATE,DELETE,INSERT等SQL语句。另一类是关系集群数据库可视化管理平台用户,用于管理配置信息。此…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...





