Mesh网格
Mesh(网格)
定义:Mesh 是一个包含顶点、三角形、顶点法线、UV坐标、颜色和骨骼权重等数据的对象。它定义了3D模型的几何形状。
功能:
顶点(Vertices):构成3D模型的点。
三角形(Triangles):由三个顶点组成的面,定义了模型的表面。
法线(Normals):定义了表面的朝向,对于光照计算非常重要。
UV坐标(UV Coordinates):用于将纹理映射到3D模型上。
颜色(Colors):可以为每个顶点或每个子网格指定颜色。
骨骼权重(Bone Weights):用于骨骼动画,定义了顶点如何受到骨骼的影响。
MeshRenderer
定义:MeshRenderer 是一个组件,用于在Unity场景中渲染Mesh。
功能:
渲染网格:MeshRenderer 渲染与之关联的 MeshFilter 组件中的 Mesh。
材质应用:MeshRenderer 可以应用一个或多个材质到 Mesh 上,每个子网格可以有不同的材质。
光照和阴影:处理 Mesh 的光照和阴影效果。
全局光照:与全局光照系统(如光照探针和反射探针)交互,以实现更真实的光照效果。
脚本控制:可以通过脚本来动态改变 MeshRenderer 的属性,如材质、颜色等。
MeshRenderer 依赖于 MeshFilter 组件来获取要渲染的 Mesh。MeshFilter 组件存储对 Mesh 的引用。

private Mesh m_Mesh = null;
private Vector3[] m_Vertices = null;
private int[] m_Triangles = null;void Start()
{m_Mesh = new Mesh();this.gameObject.GetComponent<MeshFilter>().mesh = m_Mesh;m_Mesh.name = "Test Mesh";m_Vertices = new Vector3[]{new Vector3(0,0,0),new Vector3(0,1,0),new Vector3(1,0,0),new Vector3(1,1,0),};m_Triangles = new int[]{0,1,2,2,1,3}m_Mesh.Clear();m_Mesh.vertices = m_Vertices;m_Mesh.triangles = m_Triangles;}

相关文章:

Mesh网格
Mesh(网格) 定义:Mesh 是一个包含顶点、三角形、顶点法线、UV坐标、颜色和骨骼权重等数据的对象。它定义了3D模型的几何形状。 功能: 顶点(Vertices):构成3D模型的点。 三角形(Triangles)&…...

LeetCode 509.斐波那契数
动态规划思想 五步骤: 1.确定dp[i]含义 2.递推公式 3.初始化 4.遍历顺序 5.打印dp数组 利用状态压缩,简化空间复杂度。在原代码中,dp 数组保存了所有状态,但实际上斐波那契数列的计算只需要前两个状态。因此,我们…...

SQL Server 数据太多如何优化
大家好,我是 V 哥。讲了很多数据库,有小伙伴说,SQL Server 也讲一讲啊,好吧,V 哥做个听话的门童,今天要聊一聊 SQL Server。 在 SQL Server 中,当数据量增大时,数据库的性能可能会受…...

关于word 页眉页脚的一些小问题
去掉页眉底纹: 对文档的段落边框和底纹进行设置,也是页眉横线怎么删除的一种解决方式,具体操作如下: 选中页眉中的横线文本; 点击【开始】选项卡,在【段落】组中点击【边框】按钮的下拉箭头; …...

【高等数学学习记录】连续函数的运算与初等函数的连续性
一、知识点 (一)连续函数的和、差、积、商的连续性 定理1 设函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,则它们的和(差) f g f\pm g fg、积 f ⋅ g f\cdot g f⋅g 及商 f g \frac{f…...

【抖音直播间弹幕】protobuf协议分析
将Uint8Array变成 PushFrame格式,里面的payload就存放着弹幕消息 点进去就可以看到其定义的proto结构 headers是一个自定义类型 将测试数据保存一下,等下做对比 先将PushFrame的 payload 内容进行gzip解压 然后再解析为响应 可以看到里面有对应的消…...
)
Swift 开发教程系列 - 第11章:内存管理和 ARC(Automatic Reference Counting)
在 Swift 中,内存管理由 ARC(自动引用计数)机制自动处理。ARC 通过追踪和管理对象的引用计数来确保分配的内存得到有效释放。尽管 ARC 在大多数情况下能够高效地管理内存,但理解其工作原理仍然十分重要,因为不当的引用…...

C#中 layout的用法
在C#中,layout并不是一个直接用于C#语言本身的关键字或特性。然而,layout在与C#紧密相关的某些上下文中确实有其用途,特别是在涉及用户界面(UI)设计和数据展示时。以下是几个常见的与layout相关的用法场景:…...

【编程概念基础知识】
、编程基础 一、面向对象的三大特性 1、封装: 盒子、零件、按钮 隐藏对象 的内部状态,并且只通过对象的方法来访问数据 想象你有一个小盒子(这个盒子就是一个类),里面装着一些零件(这些零件就是数据&a…...

【React】深入理解 JSX语法
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 深入理解 JSX语法1. JSX 简介2. JSX 的基本语法2.1 基本结构2.2 与普通 JavaScr…...

【Linux】从零开始使用多路转接IO --- 理解EPOLL的 LT水平触发模式 与 ET边缘触发模式
当你偶尔发现语言变得无力时, 不妨安静下来, 让沉默替你发声。 --- 里则林 --- 从零开始认识多路转接 1 EPOLL优缺点2 EPOLL工作模式 1 EPOLL优缺点 poll 的优点(和 select 的缺点对应) 接口使用方便:虽然拆分成了三个函数,…...

QtLua
描述 QtLua 库旨在使用 Lua 脚本语言使 Qt4/Qt5 应用程序可编写脚本。它是 QtScript 模块的替代品。 QtLua 不会为 Qt 生成或使用生成的绑定代码。相反,它提供了有用的 C 包装器类,使 C 和 lua 对象都可以从 lua 和 C 访问。它利用 Qt 元对象系统将 QOb…...

c++-有关计数、双变量累加、半衰、阶乘、变量值互换的基础知识
C是一种非常强大和灵活的编程语言,它包含了许多重要的概念和技巧。在本文中,我们将重点讨论五个主题:计数、双变量累加、半衰、阶乘和变量值的互换。我们将介绍这些概念的定义、用法、题目、答案和解释,以帮助读者更好地理解和运用…...
MyBatis3-获取参数值的方式、查询功能及特殊SQL执行
目录 准备工作 获取参数值的方式(重点) 查询功能 查询一个实体类对象 查询一个list集合 查询单个数据 查询一条数据为map集合 查询多条数据为map集合 特殊SQL执行 模糊查询 批量删除 动态设置表名 添加功能获取自增的主键 准备工作 模块My…...
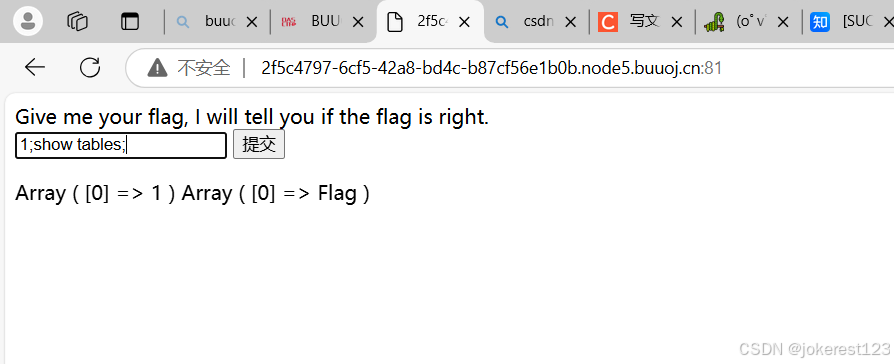
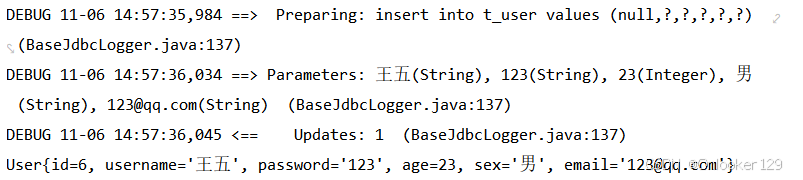
web——[SUCTF 2019]EasySQL1——堆叠注入
这个题主要是讲述了堆叠注入的用法,来复现一下 什么是堆叠注入 堆叠注入:将多条SQL语句放在一起,并用分号;隔开。 1.查看数据库的名称 查看数据库名称 1;show databases; 发现有名称为ctftraining的数据库 2.对表进行查询 1;show tabl…...
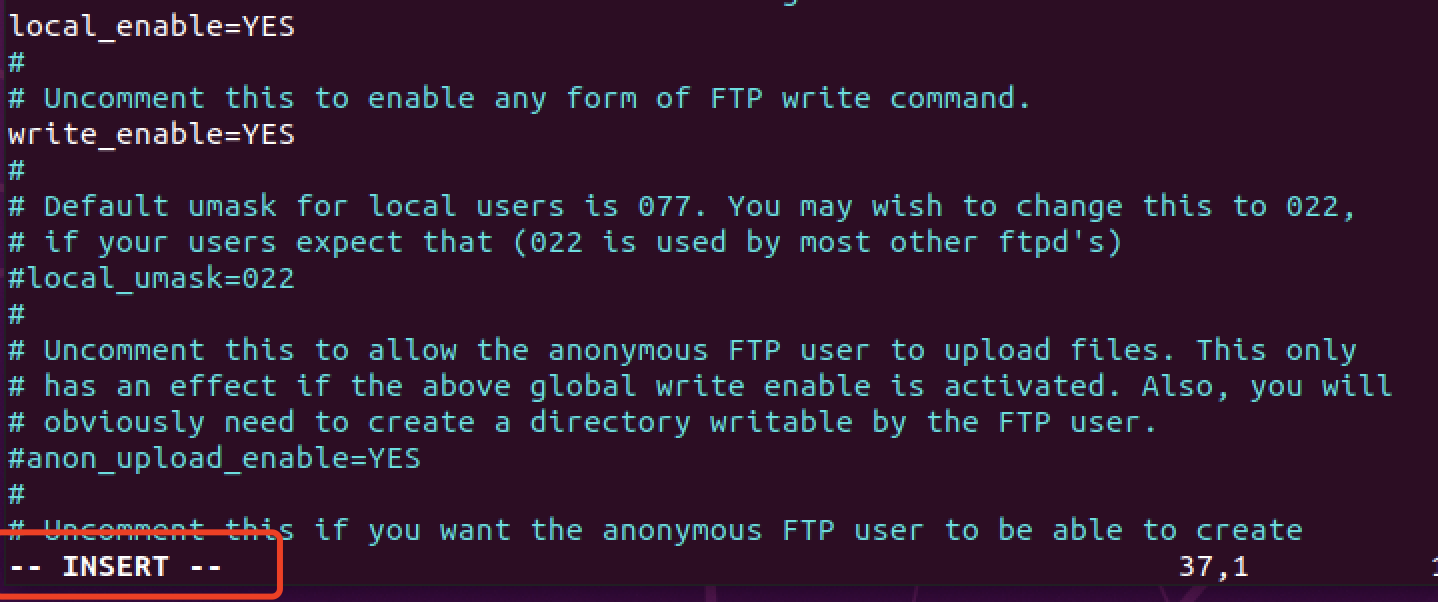
【Ubuntu学习】Ubuntu无法使用vim命令编辑
问题 在VMware首次安装Ubuntu,使用vi指令对文件进行编辑,按i键后无法更改文件内容。 原因 由于Ubuntu中预装的是vim-tiny,平时开发中需要使用vim-full。 解决方案 卸载预装vim sudo apt-get remove vim-common安装vim-full sudo apt-get …...
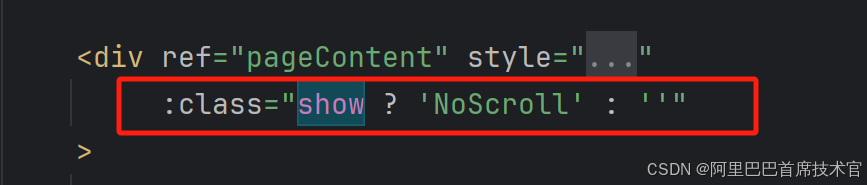
UniAPP u-popup 禁止背景滑动
增加class .NoScroll {overflow: hidden;position: fixed; }在外层div上增加该class判断条件...

F5全新报告揭示AI时代API安全面临严峻挑战
F5 《2024年应用策略现状报告:API安全》揭示了 API 保护中的漏洞以及对全面安全措施的迫切需求 西雅图,2024年11月11日 – F5(NASDAQ: FFIV)日前发布《2024年应用策略现状报告:API 安全》(以下简称为“报告”),揭示了跨行业API安全面临的严峻现状。该报告强调了企业API保护方面…...

使用C语言进行信号处理:从理论到实践的全面指南
1. 引言 在现代操作系统中,信号是一种进程间通信机制,它允许操作系统或其他进程向一个进程发送消息。信号可以用来通知进程发生了一些重要事件,如用户请求终止进程、硬件异常、定时器超时等。掌握信号处理技术对于开发健壮、高效的系统程序至…...
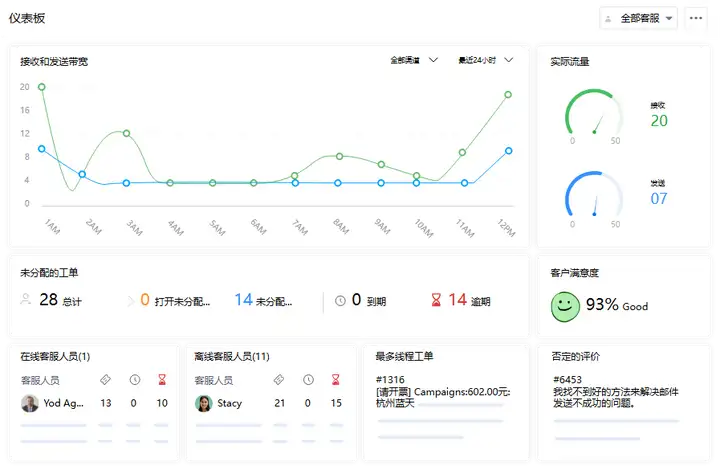
什么是工单管理系统?全面认识指南
在现代企业中,客户服务和支持是业务成功的关键因素之一。为了有效地管理客户请求和问题,许多公司采用了工单管理系统。本文将深入探讨工单管理系统的定义、功能、优势。 一、工单管理系统的定义 工单管理系统是一种软件工具,旨在帮助企业管…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
