【高等数学学习记录】连续函数的运算与初等函数的连续性
一、知识点
(一)连续函数的和、差、积、商的连续性
- 定理1
设函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,则它们的和(差) f ± g f\pm g f±g、积 f ⋅ g f\cdot g f⋅g 及商 f g \frac{f}{g} gf(当 g ( x 0 ) ≠ 0 g(x_0)\neq 0 g(x0)=0 时)都在点 x 0 x_0 x0 连续.
(二)反函数与复合函数的连续性
- 定理2
如果函数 y = f ( x ) y=f(x) y=f(x) 在区间 I x I_x Ix 上单调增加(或单调减少)且连续,那么它的反函数 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y) 也在对应的区间 I y = { y ∣ y = f ( x ) , x ∈ I x } I_y=\lbrace y|y=f(x),x\in I_x\rbrace Iy={y∣y=f(x),x∈Ix} 上单调增加(或单调减少)且连续.
- 定理3
设函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)] 由函数 u = g ( x ) u=g(x) u=g(x) 与函数 y = f ( u ) y=f(u) y=f(u) 复合而成, U ˚ ( x 0 ) ⊂ D f ⋅ g \mathring{U}(x_0)\subset D_{f\cdot g} U˚(x0)⊂Df⋅g. 若 lim x → x 0 g ( x ) = u 0 \lim_{x\rightarrow x_0}g(x)=u_0 limx→x0g(x)=u0,而函数 y = f ( u ) y=f(u) y=f(u) 在 u = u 0 u=u_0 u=u0 连续,则 lim x → x 0 f [ g ( x ) ] = lim u → u 0 f ( u ) = f ( u 0 ) \lim_{x\rightarrow x_0}f[g(x)]=\lim_{u\rightarrow u_0}f(u)=f(u_0) limx→x0f[g(x)]=limu→u0f(u)=f(u0).
- 定理4
设函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)] 是由函数 u = g ( x ) u=g(x) u=g(x) 与函数 y = f ( u ) y=f(u) y=f(u) 复合而成, U ( x 0 ) ⊂ D f ⋅ g U(x_0)\subset D_{f\cdot g} U(x0)⊂Df⋅g. 若函数 u = g ( x ) u=g(x) u=g(x) 在 x = x 0 x=x_0 x=x0 连续,且 g ( x 0 ) = u 0 g(x_0)=u_0 g(x0)=u0, 而函数 y = f ( u ) y=f(u) y=f(u) 在 u = u 0 u=u_0 u=u0 连续,则复合函数 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)] 在 x = x 0 x=x_0 x=x0 也连续.
(三)初等函数的连续性
- 一切初等函数在其定义区间内都是连续的。所谓定义区间,就是包含在定义域内的区间。
二、练习题
- 求函数 f ( x ) = x 3 + 3 x 2 − x − 3 x 2 + x − 6 f(x)=\frac{x^3+3x^2-x-3}{x^2+x-6} f(x)=x2+x−6x3+3x2−x−3 的连续区间,并求极限 lim x → 0 f ( x ) \lim_{x\rightarrow 0}f(x) limx→0f(x), lim x → − 3 f ( x ) \lim_{x\rightarrow -3}f(x) limx→−3f(x) 及 lim x → 2 f ( x ) \lim_{x\rightarrow 2}f(x) limx→2f(x).
- 解答:
∵ f ( x ) = ( x + 3 ) ( x + 1 ) ( x − 1 ) ( x + 3 ) ( x − 2 ) \because f(x)=\frac{(x+3)(x+1)(x-1)}{(x+3)(x-2)} ∵f(x)=(x+3)(x−2)(x+3)(x+1)(x−1) 在 x = − 3 x=-3 x=−3 和 x = 2 x=2 x=2 上没有定义
∵ \because ∵ 一切初等函数在其定义区间内都是连续的
∴ f ( x ) \therefore f(x) ∴f(x) 的连续区间为 ( − ∞ , − 3 ) (-\infty, -3) (−∞,−3), ( − 3 , 2 ) (-3,2) (−3,2), ( 2 , + ∞ ) (2, +\infty) (2,+∞).
lim x → 0 f ( x ) = lim x → 0 − 3 − 6 = 1 2 \lim_{x\rightarrow 0}f(x)=\lim_{x\rightarrow 0}\frac{-3}{-6}=\frac{1}{2} limx→0f(x)=limx→0−6−3=21
lim x → − 3 f ( x ) = lim x → − 3 ( − 2 ) ⋅ ( − 4 ) − 5 = − 8 5 \lim_{x\rightarrow -3}f(x)=\lim_{x\rightarrow -3}\frac{(-2)\cdot (-4)}{-5}=-\frac{8}{5} limx→−3f(x)=limx→−3−5(−2)⋅(−4)=−58
lim x → 2 f ( x ) = lim x → 2 ( x + 1 ) ( x − 1 ) x − 2 = ∞ \lim_{x\rightarrow 2}f(x)=\lim_{x\rightarrow 2}\frac{(x+1)(x-1)}{x-2}=\infty limx→2f(x)=limx→2x−2(x+1)(x−1)=∞
- 设函数 f ( x ) f(x) f(x) 与 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,证明函数: φ ( x ) = m a x { f ( x ) , g ( x ) } \varphi(x)=max\lbrace f(x),g(x)\rbrace φ(x)=max{f(x),g(x)}, ψ ( x ) = m i n { f ( x ) , g ( x ) } \psi (x)=min\lbrace f(x),g(x) \rbrace ψ(x)=min{f(x),g(x)} 在点 x 0 x_0 x0 也连续.
- 解答:
根据定理1:
∵ \because ∵ 函数 f ( x ) f(x) f(x) 与 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,而
φ ( x ) = [ f ( x ) + g ( x ) + ∣ f ( x ) − g ( x ) ∣ ] / 2 \quad \varphi (x)=[f(x)+g(x)+\begin{vmatrix}f(x)-g(x)\end{vmatrix}]/2 φ(x)=[f(x)+g(x)+∣∣f(x)−g(x)∣∣]/2
ψ ( x ) = [ f ( x ) + g ( x ) − ∣ f ( x ) − g ( x ) ∣ ] / 2 \quad \psi(x)=[f(x)+g(x)-\begin{vmatrix}f(x)-g(x)\end{vmatrix}]/2 ψ(x)=[f(x)+g(x)−∣∣f(x)−g(x)∣∣]/2
∴ φ ( x ) \therefore \varphi (x) ∴φ(x) 与 ψ ( x ) \psi(x) ψ(x) 在点 x 0 x_0 x0 也连续.
- 求下列极限:
(1) lim x → 0 x 2 − 2 x + 5 \lim_{x\rightarrow 0}\sqrt{x^2-2x+5} limx→0x2−2x+5
(2) lim α → π 4 ( s i n 2 α ) 3 \lim_{\alpha \rightarrow \frac{\pi}{4}}(sin2\alpha)^3 limα→4π(sin2α)3
(3) lim x → π 6 l n ( 2 c o s 2 x ) \lim_{x\rightarrow \frac{\pi}{6}}ln(2cos2x) limx→6πln(2cos2x)
(4) lim x → 0 x + 1 − 1 x \lim_{x\rightarrow 0}\frac{\sqrt{x+1}-1}{x} limx→0xx+1−1
(5) lim x → 1 5 x − 4 − x x − 1 \lim_{x\rightarrow 1}\frac{\sqrt{5x-4}-\sqrt{x}}{x-1} limx→1x−15x−4−x
(6) lim x → α s i n x − s i n α x − α \lim_{x\rightarrow \alpha}\frac{sinx-sin\alpha}{x-\alpha} limx→αx−αsinx−sinα
(7) lim x → + ∞ ( x 2 + x − x 2 − x ) \lim_{x\rightarrow +\infty}(\sqrt{x^2+x}-\sqrt{x^2-x}) limx→+∞(x2+x−x2−x)
- 解答:
- (1)
lim x → 0 x 2 − 2 x + 5 = 0 − 0 + 5 = 5 \lim_{x\rightarrow 0}\sqrt{x^2-2x+5}=\sqrt{0-0+5}=\sqrt{5} limx→0x2−2x+5=0−0+5=5 - (2)
lim α → π 4 ( s i n 2 α ) 3 = [ s i n ( 2 ⋅ π 4 ) ] 3 = 1 \lim_{\alpha\rightarrow \frac{\pi}{4}}(sin2\alpha)^3=[sin(2\cdot \frac{\pi}{4})]^3=1 limα→4π(sin2α)3=[sin(2⋅4π)]3=1 - (3)
lim x → π 6 l n ( 2 c o s 2 x ) = l n ( 2 c o s ( 2 ⋅ π 6 ) ) = l n 1 = 0 \lim_{x\rightarrow \frac{\pi}{6}}ln(2cos2x)=ln(2cos(2\cdot \frac{\pi}{6}))=ln1=0 limx→6πln(2cos2x)=ln(2cos(2⋅6π))=ln1=0 - (4)
lim x → 0 x + 1 − 1 x = lim x → 0 ( x + 1 − 1 ) ( x + 1 + 1 ) x ( x + 1 + 1 ) = 1 0 + 1 + 1 = 1 2 \lim_{x\rightarrow 0}\frac{\sqrt{x+1}-1}{x}=\lim_{x\rightarrow 0}\frac{(\sqrt{x+1}-1)(\sqrt{x+1}+1)}{x(\sqrt{x+1}+1)}=\frac{1}{\sqrt{0+1}+1}=\frac{1}{2} limx→0xx+1−1=limx→0x(x+1+1)(x+1−1)(x+1+1)=0+1+11=21 - (5)
lim x → 1 5 x − 4 − x x − 1 = lim x → 1 ( 5 x − 4 − x ) ( 5 x − 4 + x ) ( x − 1 ) ( 5 x − 4 + x ) = lim x → 1 4 5 x − 4 + x = 2 \lim_{x\rightarrow 1}\frac{\sqrt{5x-4}-\sqrt{x}}{x-1}=\lim_{x\rightarrow 1}\frac{(\sqrt{5x-4}-\sqrt{x})(\sqrt{5x-4}+\sqrt{x})}{(x-1)(\sqrt{5x-4}+\sqrt{x})}=\lim_{x\rightarrow 1}\frac{4}{\sqrt{5x-4}+\sqrt{x}}=2 limx→1x−15x−4−x=limx→1(x−1)(5x−4+x)(5x−4−x)(5x−4+x)=limx→15x−4+x4=2 - (6)
lim x → α s i n x − s i n α x − α = lim x → α 2 ⋅ c o s x + α 2 ⋅ s i n x − α 2 x − α = lim x → α c o s x + α 2 = c o s α \lim_{x\rightarrow \alpha}\frac{sinx-sin\alpha}{x-\alpha}=\lim_{x\rightarrow \alpha}\frac{2\cdot cos\frac{x+\alpha}{2} \cdot sin \frac{x-\alpha}{2}}{x-\alpha}=\lim_{x\rightarrow \alpha}cos\frac{x+\alpha}{2}=cos\alpha limx→αx−αsinx−sinα=limx→αx−α2⋅cos2x+α⋅sin2x−α=limx→αcos2x+α=cosα - (7)
lim x → + ∞ ( x 2 + x − x 2 − x ) = lim x → + ∞ ( x 2 + x − x 2 − x ) ( x 2 + x + x 2 − x ) x 2 + x + x 2 − x = lim x → + ∞ 2 x x 2 + x + x 2 − x = lim x → + ∞ 2 1 + 1 x + 1 − 1 x = 1 \lim_{x\rightarrow +\infty}(\sqrt{x^2+x}-\sqrt{x^2-x})=\lim_{x\rightarrow +\infty}\frac{(\sqrt{x^2+x}-\sqrt{x^2-x})(\sqrt{x^2+x}+\sqrt{x^2-x})}{\sqrt{x^2+x}+\sqrt{x^2-x}}=\lim_{x\rightarrow +\infty}\frac{2x}{\sqrt{x^2+x}+\sqrt{x^2-x}}=\lim_{x\rightarrow +\infty}\frac{2}{\sqrt{1+\frac{1}{x}}+\sqrt{1-\frac{1}{x}}}=1 limx→+∞(x2+x−x2−x)=limx→+∞x2+x+x2−x(x2+x−x2−x)(x2+x+x2−x)=limx→+∞x2+x+x2−x2x=limx→+∞1+x1+1−x12=1
- 求下列极限:
(1) lim x → ∞ e 1 x \lim_{x\rightarrow \infty}e^{\frac{1}{x}} limx→∞ex1
(2) lim x → 0 l n s i n x x \lim_{x\rightarrow 0}ln\frac{sinx}{x} limx→0lnxsinx
(3) lim x → ∞ ( 1 + 1 x ) x 2 \lim_{x\rightarrow\infty}(1+\frac{1}{x})^{\frac{x}{2}} limx→∞(1+x1)2x
(4) lim x → 0 ( 1 + 3 t a n 2 x ) c o t 2 x \lim_{x\rightarrow 0}(1+3tan^2x)^{cot^2x} limx→0(1+3tan2x)cot2x
(5) lim x → ∞ ( 3 + x 6 + x ) x − 1 2 \lim_{x\rightarrow \infty}(\frac{3+x}{6+x})^{\frac{x-1}{2}} limx→∞(6+x3+x)2x−1
(6) lim x → 0 1 + t a n x − 1 + s i n x x 1 + s i n 2 x − x \lim_{x\rightarrow 0}\frac{\sqrt{1+tanx}-\sqrt{1+sinx}}{x\sqrt{1+sin^2x}-x} limx→0x1+sin2x−x1+tanx−1+sinx
- 解答:
- (1)
lim x → ∞ e 1 x = e lim x → ∞ 1 x = e 0 = 1 \lim_{x\rightarrow \infty}e^{\frac{1}{x}}=e^{\lim_{x\rightarrow \infty}\frac{1}{x}}=e^0=1 limx→∞ex1=elimx→∞x1=e0=1 - (2)
lim x → 0 l n s i n x x = l n lim x → 0 s i n x x = l n 1 = 0 \lim_{x\rightarrow 0}ln\frac{sinx}{x}=ln\lim_{x\rightarrow 0}\frac{sinx}{x}=ln1=0 limx→0lnxsinx=lnlimx→0xsinx=ln1=0 - (3)
lim x → ∞ ( 1 + 1 x ) x 2 = [ lim x → ∞ ( 1 + 1 x ) x ] 1 2 = e 1 2 \lim_{x\rightarrow \infty}(1+\frac{1}{x})^{\frac{x}{2}}=[\lim_{x\rightarrow \infty}(1+\frac{1}{x})^x]^{\frac{1}{2}}=e^{\frac{1}{2}} limx→∞(1+x1)2x=[limx→∞(1+x1)x]21=e21 - (4)
lim x → 0 ( 1 + 3 ⋅ t a n 2 x ) c o t 2 x \lim_{x\rightarrow 0}(1+3\cdot tan^2x)^{cot^2x} limx→0(1+3⋅tan2x)cot2x(令 t = 3 ⋅ t a n 2 x t=3\cdot tan^2x t=3⋅tan2x) = lim t → 0 + ( 1 + t ) 3 t =\lim_{t\rightarrow 0^+}(1+t)^\frac{3}{t} =limt→0+(1+t)t3(令 u = 1 t u=\frac{1}{t} u=t1) = [ lim u → + ∞ ( 1 + 1 u ) u ] 3 = e 3 =[\lim_{u\rightarrow +\infty}(1+\frac{1}{u})^u]^3=e^3 =[limu→+∞(1+u1)u]3=e3 - (5)
lim x → ∞ ( 3 + x 6 + x ) x − 1 2 = lim x → ∞ ( 1 + − 3 6 + x ) 6 + x − 3 ⋅ − 3 6 + x ⋅ x − 1 2 = e lim x → ∞ 3 6 + x ⋅ 1 − x 2 = e 3 2 \lim_{x\rightarrow \infty}(\frac{3+x}{6+x})^{\frac{x-1}{2}}=\lim_{x\rightarrow \infty}(1+\frac{-3}{6+x})^{\frac{6+x}{-3}\cdot \frac{-3}{6+x} \cdot \frac{x-1}{2}}=e^{\lim_{x\rightarrow \infty}\frac{3}{6+x}\cdot \frac{1-x}{2}}=e^{\frac{3}{2}} limx→∞(6+x3+x)2x−1=limx→∞(1+6+x−3)−36+x⋅6+x−3⋅2x−1=elimx→∞6+x3⋅21−x=e23 - (6)
lim x → 0 1 + t a n x − 1 + s i n x x 1 + s i n 2 x − x = lim x → 0 ( x 1 + s i n 2 x + x ) ( t a n x − s i n x ) ( 1 + t a n x + 1 + s i n x ) ⋅ x 2 s i n 2 x = lim x → 0 ( 1 + s i n 2 x + 1 ) ( s e c x − 1 ) ( 1 + t a n x + 1 + s i n x ) ⋅ x s i n x = lim x → 0 2 s i n 2 x 2 x ⋅ s i n x ⋅ c o s x = 1 2 \lim_{x\rightarrow 0}\frac{\sqrt{1+tanx}-\sqrt{1+sinx}}{x\sqrt{1+sin^2x}-x}=\lim_{x\rightarrow 0}\frac{(x\sqrt{1+sin^2x}+x)(tanx-sinx)}{(\sqrt{1+tanx}+\sqrt{1+sinx})\cdot x^2sin^2x}=\lim_{x\rightarrow 0}\frac{(\sqrt{1+sin^2x}+1)(secx-1)}{(\sqrt{1+tanx}+\sqrt{1+sinx})\cdot xsinx}=\lim_{x\rightarrow 0}\frac{2sin^2\frac{x}{2}}{x\cdot sinx \cdot cosx}=\frac{1}{2} limx→0x1+sin2x−x1+tanx−1+sinx=limx→0(1+tanx+1+sinx)⋅x2sin2x(x1+sin2x+x)(tanx−sinx)=limx→0(1+tanx+1+sinx)⋅xsinx(1+sin2x+1)(secx−1)=limx→0x⋅sinx⋅cosx2sin22x=21
- 设 f ( x ) f(x) f(x) 在 R R R 上连续,且 f ( x ) ≠ 0 f(x)\neq 0 f(x)=0, φ ( x ) \varphi(x) φ(x) 在 R R R 上有定义,且有间断点,则下列陈述中哪些是对的,哪些是错的?如果是对的,说明理由;如果是错的,试给出一个反例.
(1) φ [ f ( x ) ] \varphi[f(x)] φ[f(x)] 必有间断点
(2) [ φ ( x ) ] 2 [\varphi(x)]^2 [φ(x)]2 必有间断点
(3) f [ φ ( x ) ] f[\varphi(x)] f[φ(x)] 未必有间断点
(4) φ ( x ) f ( x ) \frac{\varphi(x)}{f(x)} f(x)φ(x) 必有间断点
-
解答:
-
(1)
错。
如:
f ( x ) = 1 f(x)=1 f(x)=1
φ ( x ) = { x + 1 , x ≥ 0 x − 1 , x < 0 \varphi(x)=\begin{cases}x+1,&x\geq 0\\x-1,&x<0\end{cases} φ(x)={x+1,x−1,x≥0x<0
φ ( x ) = 2 \varphi(x)=2 φ(x)=2 在 R R R上连续,没有间断点. -
(2)
错。
如:
φ ( x ) = { 1 , x ≥ 0 − 1 , x < 0 \varphi(x)=\begin{cases}1,&x\geq 0\\-1,&x<0\end{cases} φ(x)={1,−1,x≥0x<0
[ φ ( x ) ] 2 = 1 [\varphi(x)]^2=1 [φ(x)]2=1 在 R R R 上连续,没有间断点. -
(3)
对。
如 (1) , f [ φ ( x ) ] = 1 f[\varphi(x)]=1 f[φ(x)]=1,在 R R R 上连续,没有间断点. -
(4)
对。
设 F ( x ) = φ ( x ) f ( x ) F(x)=\frac{\varphi(x)}{f(x)} F(x)=f(x)φ(x) 在 R R R 上连续。
φ ( x ) = F ( x ) ⋅ f ( x ) \varphi(x)=F(x)\cdot f(x) φ(x)=F(x)⋅f(x) 在 R R R 上连续,这与题目中给定的条件矛盾
∴ φ ( x ) f ( x ) \therefore \frac{\varphi(x)}{f(x)} ∴f(x)φ(x) 在 R R R 上有间断点.
- 设函数 f ( x ) = { e x , x < 0 a + x , x ≥ 0 f(x)=\begin{cases}e^x,&x<0\\a+x,&x\geq 0\end{cases} f(x)={ex,a+x,x<0x≥0
应当怎样选择数 a a a,使得 f ( x ) f(x) f(x) 成为在 ( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞) 内的连续函数.
- 解答:
lim x → 0 − f ( x ) = lim x → 0 − e x = 1 \lim_{x\rightarrow 0^-}f(x)=\lim_{x\rightarrow 0^-}e^x=1 limx→0−f(x)=limx→0−ex=1
lim x → 0 + f ( x ) = lim x → 0 + ( a + x ) = a \lim_{x\rightarrow 0^+}f(x)=\lim_{x\rightarrow 0^+}(a+x)=a limx→0+f(x)=limx→0+(a+x)=a
当 a = 1 a=1 a=1 时, lim x → 0 − f ( x ) = lim x → 0 + f ( x ) \lim_{x\rightarrow 0^-}f(x)=\lim_{x\rightarrow 0^+}f(x) limx→0−f(x)=limx→0+f(x), f ( x ) f(x) f(x) 在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 内连续.
- 学习资料
1.《高等数学(第六版)》 上册,同济大学数学系 编
作者感言:感谢您的关注,更欢迎您的批评和指正!
相关文章:

【高等数学学习记录】连续函数的运算与初等函数的连续性
一、知识点 (一)连续函数的和、差、积、商的连续性 定理1 设函数 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 在点 x 0 x_0 x0 连续,则它们的和(差) f g f\pm g fg、积 f ⋅ g f\cdot g f⋅g 及商 f g \frac{f…...

【抖音直播间弹幕】protobuf协议分析
将Uint8Array变成 PushFrame格式,里面的payload就存放着弹幕消息 点进去就可以看到其定义的proto结构 headers是一个自定义类型 将测试数据保存一下,等下做对比 先将PushFrame的 payload 内容进行gzip解压 然后再解析为响应 可以看到里面有对应的消…...
)
Swift 开发教程系列 - 第11章:内存管理和 ARC(Automatic Reference Counting)
在 Swift 中,内存管理由 ARC(自动引用计数)机制自动处理。ARC 通过追踪和管理对象的引用计数来确保分配的内存得到有效释放。尽管 ARC 在大多数情况下能够高效地管理内存,但理解其工作原理仍然十分重要,因为不当的引用…...

C#中 layout的用法
在C#中,layout并不是一个直接用于C#语言本身的关键字或特性。然而,layout在与C#紧密相关的某些上下文中确实有其用途,特别是在涉及用户界面(UI)设计和数据展示时。以下是几个常见的与layout相关的用法场景:…...

【编程概念基础知识】
、编程基础 一、面向对象的三大特性 1、封装: 盒子、零件、按钮 隐藏对象 的内部状态,并且只通过对象的方法来访问数据 想象你有一个小盒子(这个盒子就是一个类),里面装着一些零件(这些零件就是数据&a…...

【React】深入理解 JSX语法
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 深入理解 JSX语法1. JSX 简介2. JSX 的基本语法2.1 基本结构2.2 与普通 JavaScr…...

【Linux】从零开始使用多路转接IO --- 理解EPOLL的 LT水平触发模式 与 ET边缘触发模式
当你偶尔发现语言变得无力时, 不妨安静下来, 让沉默替你发声。 --- 里则林 --- 从零开始认识多路转接 1 EPOLL优缺点2 EPOLL工作模式 1 EPOLL优缺点 poll 的优点(和 select 的缺点对应) 接口使用方便:虽然拆分成了三个函数,…...

QtLua
描述 QtLua 库旨在使用 Lua 脚本语言使 Qt4/Qt5 应用程序可编写脚本。它是 QtScript 模块的替代品。 QtLua 不会为 Qt 生成或使用生成的绑定代码。相反,它提供了有用的 C 包装器类,使 C 和 lua 对象都可以从 lua 和 C 访问。它利用 Qt 元对象系统将 QOb…...

c++-有关计数、双变量累加、半衰、阶乘、变量值互换的基础知识
C是一种非常强大和灵活的编程语言,它包含了许多重要的概念和技巧。在本文中,我们将重点讨论五个主题:计数、双变量累加、半衰、阶乘和变量值的互换。我们将介绍这些概念的定义、用法、题目、答案和解释,以帮助读者更好地理解和运用…...
MyBatis3-获取参数值的方式、查询功能及特殊SQL执行
目录 准备工作 获取参数值的方式(重点) 查询功能 查询一个实体类对象 查询一个list集合 查询单个数据 查询一条数据为map集合 查询多条数据为map集合 特殊SQL执行 模糊查询 批量删除 动态设置表名 添加功能获取自增的主键 准备工作 模块My…...
web——[SUCTF 2019]EasySQL1——堆叠注入
这个题主要是讲述了堆叠注入的用法,来复现一下 什么是堆叠注入 堆叠注入:将多条SQL语句放在一起,并用分号;隔开。 1.查看数据库的名称 查看数据库名称 1;show databases; 发现有名称为ctftraining的数据库 2.对表进行查询 1;show tabl…...
【Ubuntu学习】Ubuntu无法使用vim命令编辑
问题 在VMware首次安装Ubuntu,使用vi指令对文件进行编辑,按i键后无法更改文件内容。 原因 由于Ubuntu中预装的是vim-tiny,平时开发中需要使用vim-full。 解决方案 卸载预装vim sudo apt-get remove vim-common安装vim-full sudo apt-get …...
UniAPP u-popup 禁止背景滑动
增加class .NoScroll {overflow: hidden;position: fixed; }在外层div上增加该class判断条件...

F5全新报告揭示AI时代API安全面临严峻挑战
F5 《2024年应用策略现状报告:API安全》揭示了 API 保护中的漏洞以及对全面安全措施的迫切需求 西雅图,2024年11月11日 – F5(NASDAQ: FFIV)日前发布《2024年应用策略现状报告:API 安全》(以下简称为“报告”),揭示了跨行业API安全面临的严峻现状。该报告强调了企业API保护方面…...

使用C语言进行信号处理:从理论到实践的全面指南
1. 引言 在现代操作系统中,信号是一种进程间通信机制,它允许操作系统或其他进程向一个进程发送消息。信号可以用来通知进程发生了一些重要事件,如用户请求终止进程、硬件异常、定时器超时等。掌握信号处理技术对于开发健壮、高效的系统程序至…...
什么是工单管理系统?全面认识指南
在现代企业中,客户服务和支持是业务成功的关键因素之一。为了有效地管理客户请求和问题,许多公司采用了工单管理系统。本文将深入探讨工单管理系统的定义、功能、优势。 一、工单管理系统的定义 工单管理系统是一种软件工具,旨在帮助企业管…...

集群化消息服务解决方案
目录 集群化消息服务解决方案项目概述架构图使用说明服务端通过API接口推送消息给客户端调用方式 请求参数返回参数 客户端推送消息连接websocket或发送消息 接收消息项目地址作者信息 集群化消息服务解决方案 项目概述 集群化消息服务解决方案是一种用于处理大量消息的高可用…...
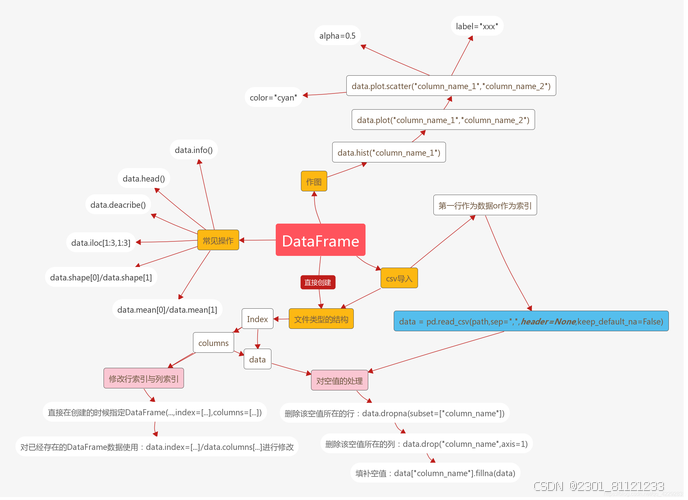
python数据结构操作与可视化的应用
Python具有丰富的数据结构操作和可视化库,可以进行各种数据结构的创建、编辑和分析,并将结果可视化。以下是几个常见的Python数据结构操作和可视化的应用示例: 1. 列表(List)操作和可视化: - 创建列表&a…...

【基于轻量型架构的WEB开发】课程 作业4 AOP
一. 单选题(共7题,38.5分) 1 (单选题)下列选项中,用于通知/增强处理的是( )。 A. Joinpoint B. Pointcut C. Aspect D. Advice 正确答案:D 答案解析:在面向切面编程ÿ…...
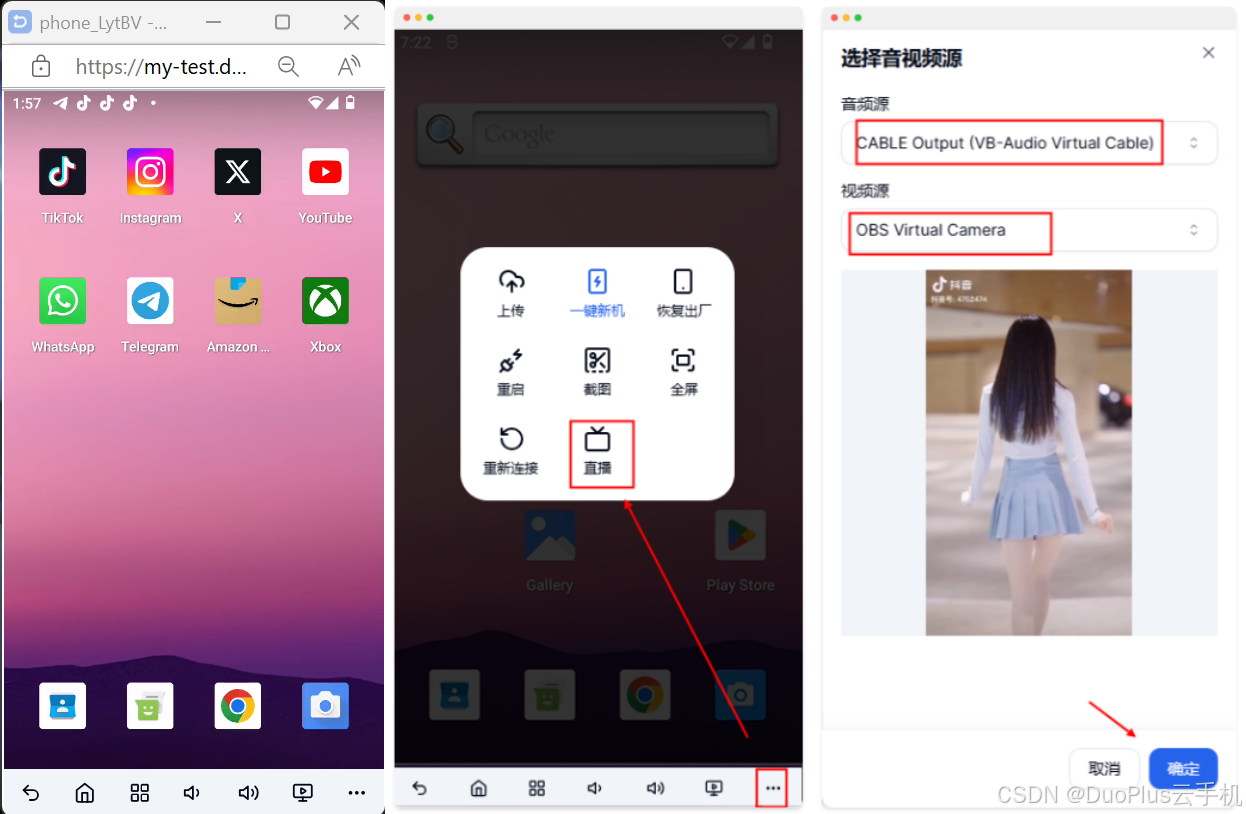
跨境独立站新手,如何用DuoPlus云手机破局海外社媒引流?
独立站作为电商领域的一个重要组成部分,其发展在最近几年里确实令人瞩目,对于想要进入跨境赛道的新手卖家来说,手上握着有优势的货源,建立小型的DTC独立站确实会比入驻第三方平台具有更大的灵活性。本文将给跨境卖家们总结独立站和…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...
