算法——移除元素(leetcode27)
对于移除元素这道题来讲,我首先想到的还是双指针,根据题目要求我们需要在给定的一组数组中找出与目标值不同的元素数量并且将与目标值不同的元素全部移至数组左边右边则不需关注数组元素的大小,我们利用两个指针一个指向数组首部位置(左指针)一个指向末端位置(右指针),如果首部位置所指元素与目标值相同则将右指针所指元素对左指针所指元素进行覆盖接着右指针向左移动如果不同则左指针向右移动重复上述步骤即可直至左指针越过右指针循环结束我们直接返回左指针下标即可(即为与目标值不同的元素数量总和)
这种方法比较正式的称呼是相向双指针法
class Solution {public int removeElement(int[] nums, int val) {int left=0;int right=nums.length-1;int sum=0;while(left<=right){if(nums[left]==val){nums[left]=nums[right];right--;} else{sum++;left++;} }return sum;}
}除此之外还有快慢指针法可以解决这个问题
快慢指针法
通过快指针来寻找与目标值不同的元素
通过慢指针来更新数组即可
class Solution {public int removeElement(int[] nums, int val) {int fastIndex=0;int slowIndex=0;while(fastIndex<=nums.length-1){if(nums[fastIndex]==val){fastIndex++;}else{nums[slowIndex]=nums[fastIndex];slowIndex++;fastIndex++;}}return slowIndex;
}
}相关文章:
)
算法——移除元素(leetcode27)
对于移除元素这道题来讲,我首先想到的还是双指针,根据题目要求我们需要在给定的一组数组中找出与目标值不同的元素数量并且将与目标值不同的元素全部移至数组左边右边则不需关注数组元素的大小,我们利用两个指针一个指向数组首部位置(左指针&…...

『OpenCV-Python』安装以及图像的读取、显示、保存
点赞 + 关注 + 收藏 = 学会了 OpenCV 是一个开源的计算机视觉库,广泛应用于图像处理、机器学习和实时计算机视觉应用。比如图像和视频的滤镜和降噪、物体检测、人脸识别、证件号识别、车牌识别等应用。当然,也有其他工具可以对这些领域做支持,但本专栏是介绍 OpenCV 的,所…...

python开发桌面应用(跨平台) 全流程
前言 之前开发一些软件,亚马逊商品分析相关软件,但是基本上是通过程序猿控制台命令启动,同时在启动之前,还要进行程序依赖包,这对于非开发人员而言,简直是一种灾难, 为了让软件对于小白更加易用, 打算将其封装成应用程序(跨平台), 下面带大家一起完成python开发桌面应用的三步…...

el-table-column prop值根据数组获取
方法一: 可以给el-table-column添加一个属性:formatter,代码如下: 这里是因为多个列都需要同样的计算,所以使用column.property获取属性,不然可以直接row.属性 方法二: 直接在template scope …...

MySQL_聚合函数分组查询
上篇复习: 设计数据库时的三大范式1.第一范式,一行数据中每一列不可再分 关系型数据库必须要满足第一范式,设计表的时候,如果每一列都可以用SQL规定的数据类型描述,就天然满足第一范式. 2.第二范式,在第一…...

PPT 制作神器!Markdown 轻松变幻灯片!
做过幻灯片的朋友们都知道,PPT 的制作常常是费时费力的工作。尤其是需要不断调整布局和设计的时候。 而现在,GitHub 上有一款开源免费的 PPT 制作工具 moffee,能够极大地简化这一过程。你只需通过简单的 Markdown 编写内容,即可快…...

一七八、Node.js PM2使用介绍
PM2 是一个强大的生产级 Node.js 进程管理器,提供了自动重启、负载均衡和进程监控等功能。适用于开发和生产环境,简化了 Node.js 应用程序的管理和维护。 PM2 安装 1. 使用 npm 安装 PM2 npm i -g pm2latest-g:全局安装。latest:…...

基于CSU18M92芯片的蓝牙体重秤方案
传统体重秤只有一个数据的显示功能,将需称重物体放置在体重秤上,体重秤显示当前物体的数据,物体移开,数据消失,体重秤没有数据记录、存储、分析功能。智能体重秤与传统体重秤相比,可通过低功耗蓝牙与手机AP…...

深度学习经典模型之VGGNet
1 VGGNet 1.1 模型介绍 VGGNet是由牛津大学视觉几何小组(Visual Geometry Group, VGG)提出的一种深层卷积网络结构,他们以7.32%的错误率赢得了2014年ILSVRC分类任务的亚军(冠军由GoogLeNet以6.65%的错误率夺得)和…...

Axure网络短剧APP端原型图,竖屏微剧视频模版40页
作品概况 页面数量:共 40 页 使用软件:Axure RP 9 及以上,非软件无源码 适用领域:短剧、微短剧、竖屏视频 作品特色 本作品为网络短剧APP的Axure原型设计图,定位属于免费短剧软件,类似红果短剧、河马剧场…...

ES + SkyWalking + Spring Boot:日志分析与服务监控(三)
目录 一、搭建SkyWalking 1.1 版本选择 1.2 下载安装 1.3 配置启动 1.4 SkyWalking UI介绍 二、Springboot项目使用 2.1 Agent下载 2.2 Agent配置skywalking oap地址 2.3 IDEA配置Agent地址 2.4 生成的ES索引介绍 三、在kibana上查看日志 四、问题和解决 3.1 日志…...

php 如何将数组转成对象数组
1. 使用 (object) 操作符: “php $array [‘name’ > ‘John’, ‘age’ > 25]; $object (object) $array; // 访问对象属性 echo $object->name; // 输出: John echo $object->age; // 输出: 25 “ 2. 使用 (stdClass): “php $array …...
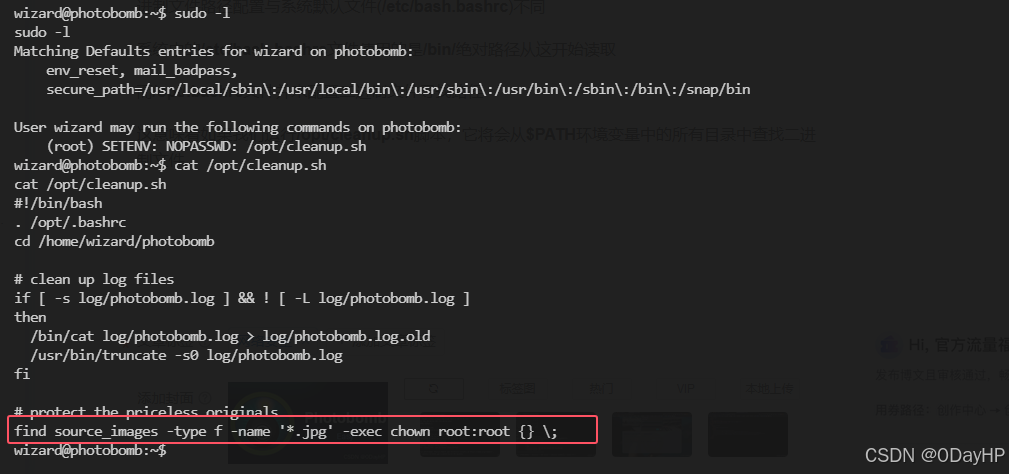
HTB:Photobomb[WriteUP]
目录 连接至HTB服务器并启动靶机 使用nmap对靶机进行端口开放扫描 再次使用nmap对靶机开放端口进行脚本、服务扫描 使用ffuf进行简单的子域名扫描 使用浏览器直接访问该域名 选取一个照片进行下载,使用Yakit进行抓包 USER_FLAG:a9afd9220ae2b5731…...

图文组合-pytorch实现
在图文组合任务中,常见的图文融合方式有多种,比如简单的拼接、加权求和、注意力机制、跨模态Transformer等。为了让图片充分补充文本的语义信息,我们可以使用一种简单且有效的图文融合方法,比如通过注意力机制。 我们可以让文本特…...

CentOS AppStream 8 手动更新 yum源
由于CentOS 8的官方支持已在2021年12月31日结束,官方镜像中的CentOS 8包已被移除。因此,如果您仍然需要运行CentOS 8并更新其yum源,您可以考虑使用以下步骤来配置一个可用的yum源,例如阿里云的镜像源。 https://mirrors.aliyun.co…...

虚拟化环境中香港服务器内存如何分配与管理?
虚拟化技术通过创建抽象层来模拟硬件资源,使得可以在单一硬件上运行多个操作系统实例。这通常涉及两个主要组件:管理程序(Hypervisor)和虚拟机监控器(VMM)。管理程序直接安装在物理硬件上,负责创建和管理虚拟机,而VMM则用于监控和…...

Android源码中如何编译出fastboot.exe和adb.exe程序
1、方案背景说明 在进行android项目开发时,如果通用的fastboot工具无法满足项目的定制话的需求时,就需要对fastboot工具的源码进行自定义修改,并编译成新的fastboot和adb工具。 由于安卓源码的的编译通常使用的是ubuntu系统,默认…...

C++ 参数传递 笔记
目录 1、输入参数的传递方式-选择传值还是传引用? 处理用户信息 处理坐标 处理配置 处理ID 2、对于需要修改的参数,使用非const引用传递 有趣的例外:警惕表象的迷惑 需要警惕的陷阱 “糟糕”的update方法: “完美”的set_name与set…...

【Linux】注释和配置文件的介绍
目录 一、help vim-modes指令 二、vim命令模式下的注释 1、直接注释: 2、快捷键注释(比较麻烦,了解即可) 三、vim的配置文件 .vimrc 四、sudo指令的相关问题 一、help vim-modes指令 在底行模式输入该指令可以用于查看vim的十…...

安卓主板_基于联发科MTK MT8788平台平板电脑方案_安卓核心板开发板定制
联发科MT8788安卓核心板平台介绍: MTK8788设备具有集成的蓝牙、fm、wlan和gps模块,是一个高度集成的基带平台,包括调制解调器和应用处理子系统,启用LTE/LTE-A和C2K智能设备应用程序。该芯片集成了工作在2.0GHz的ARM Cortex-A73、最…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
