AVL树解析
目录
一. AVL的概念
二 AVL树的插入
2.1先按二叉搜索树的规则插入
2.2 AVL的重点:平衡因子更新
3.1 更新后parent的平衡因子等于0。
3.2 更新后parent的平衡因子等于1 或 -1,需要继续往上更新。
3.3 更新后parent的平衡因子等于2 或 -2,需要使用旋转处理。
三.旋转 和 平衡因子等于2 或 -2 的处理
1.右单旋(把左孩子变成爸爸)
2.左单旋(把右孩子变成爸爸)
3.左右双旋(把LR_Child 变为爸爸)
4.左右双旋(把RL_Child 变为爸爸)
总代码:
一. AVL的概念
1.AVL树是最先发明的自平衡二叉查找树,AVL是一颗空树,或者具备下列性质的二叉搜索树:它的
左右子树都是AV树,且 左右子树的高度差的绝对值不超过1 。AVL树是一颗高度平衡搜索二叉树,通过控制高度差去控制平衡!!!
2.AVL树实现这里我们引入一个平衡因子(balance factor)的概念,每个结点都有一个平衡因子,任何结点的平衡因子等于右子树的高度减去左子树的高度,也就是说任何结点的平衡因子等于0/1/-1
AVL树并不是必须要平衡因子,但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡
就像一个风向标一样。
二 AVL树的插入
AVL节点 的大概结构 AVL树 的大概结构


2.1先按二叉搜索树的规则插入
具体可以看这篇
二叉搜索树-CSDN博客
这里是二叉搜索树的,简单的代码总结

2.2 AVL的重点:平衡因子更新
因为:左右子树的高度差的绝对值不超过1 。
这里我们可以规定
1. 平衡因子 = 右子树高度 - 左子树高度 。
2. 插入结点时,会增加高度,如果新增结点 在parent的右子树,parent的平衡因子++,新增结点在parent的左子树,parent平衡因子--,parent的平衡因子初始化为 0.
3. parent的停止更新条件分为3种:
3.1 更新后parent的平衡因子等于0。


3.2 更新后parent的平衡因子等于1 或 -1,需要继续往上更新。


上面的总代码:

3.3 更新后parent的平衡因子等于2 或 -2,需要使用旋转处理。

下面为具体的分析:
三.旋转 和 平衡因子等于2 或 -2 的处理
旋转总共分为四种,左单旋/右单旋/左右双旋/右左双旋。
这里我们规定:
1. 在parent的左边 插入孩子,parent的平衡因子 - 1
2 .在parent的右边 插入孩子,parent的平衡因子 + 1
1.右单旋(把左孩子变成爸爸)
需要 单纯的左边高!!! 才可以使用
比如 if(parent->_bf == -2 && SubR->_bf == -1)
如图:
分析:
因为 左右子树的高度差的绝对值不超过1
我们需要把 a 往上提,把parent往下压 ,让SubL变成爸爸 才可以解决。
总的来说就是,左边高就把左边提上来,把右边压下去。
在这种情况下 他们的平衡因子就会为0.
代码为:

RotateR:

2.左单旋(把右孩子变成爸爸)
需要 单纯的右边高!!! 才可以使用
比如 if(parent->_bf == 2 && SubR->_bf == 1)
如图:

分析:
因为 左右子树的高度差的绝对值不超过1
我们需要把 a 往上提,把parent往下压 ,让SubR变成爸爸 才可以解决。
总的来说就是,右边高就把右边提上来,把左边压下去。
在这种情况下 他们的平衡因子就会为0.
代码为:

RotateL:

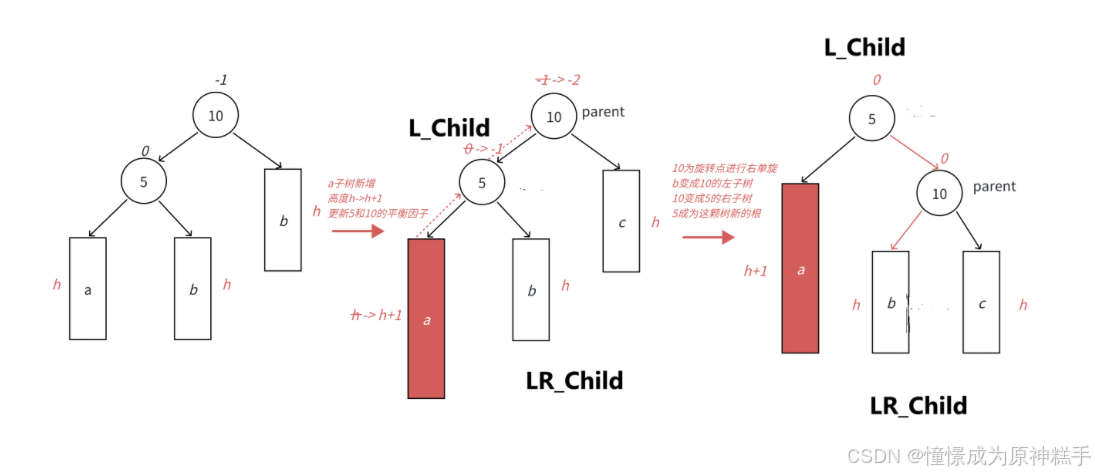
3.左右双旋(把LR_Child 变为爸爸)
需要 左边的右边高!!! 才可以使用
如图所示:

当没插入节点时:

在LR_Child 的左边插入节点:

具体过程
1. 让节点5 左旋转:

2.让节点8 右旋转

平衡因子:
在LR_Child 为空时
平衡因子 都为0.

在LR_Child 的左边插入节点:
LR_Child 平衡因子 为 0
L_Child 平衡因子 为 0
parent 平衡因子为 1
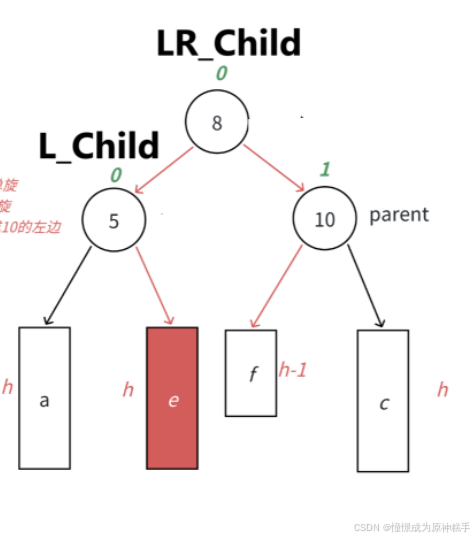
在LR_Child 的右边插入节点:
LR_Child 平衡因子 为 0
L_Child 平衡因子 为 -1
parent 平衡因子为 0

代码:


4.左右双旋(把RL_Child 变为爸爸)
太长了,随便写点了,脑子坏了!!!

在LR_Child 为空时
平衡因子 都为0.

在LR_Child 的右边插入节点:
RL_Child 平衡因子 为 0
R_Child 平衡因子 为 0
parent 平衡因子为 -1

在RL_Child 的左边插入节点:
RL_Child 平衡因子 为 0
R_Child 平衡因子 为 1
parent 平衡因子为 0

代码:


总代码:
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<class T>struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft;AVLTreeNode<T>* _pRight;AVLTreeNode<T>* _pParent;T _data;int _bf; // 节点的平衡因子
};// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:AVLTree(): _pRoot(nullptr){}// 在AVL树中插入值为data的节点bool Insert(const T& data){//如果树为空就建立一个根节点if (_pRoot == nullptr){_pRoot = new Node(data);}//树不为空else{Node* parent = nullptr;Node* tmp = _pRoot;//用cur找位置 while (tmp){//插入值比当前结点小往左走if (tmp->_data < data){parent = tmp;tmp = tmp->_pRight;}//插入值比当前结点大往右走else if (tmp->_data > data){parent = tmp;tmp = tmp->_pLeft;}else{assert(false);}}//在parent的左边或者右边插入插入Node* cur = new Node(data);if (parent->_data < data){parent->_pRight = cur;cur->_pParent = parent;}else if (parent->_data > data){parent->_pLeft = cur;cur->_pParent = parent;}//最困难的平衡因子部分while (parent){//cur插入在右边,平衡因子++if (cur == parent->_pRight)parent->_bf++;//反之亦然elseparent->_bf--;//平衡因子为0 结束if (parent->_bf == 0)break;//平衡因子为1 或 -1,往上更新else if(parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_pParent;}else if(parent->_bf == -2 || parent->_bf == 2){//...// //单纯左边高if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);parent->_bf = 0;cur->_bf = 0;}//单纯右边高else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);parent->_bf = 0;cur->_bf = 0;}//左边的右边高else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//右边的左边高else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}}return true;}// AVL树的验证bool IsAVLTree(){return _Height(_pRoot);}void InOrder(){return _InOrder(_pRoot);}size_t Height(){return _Height(_pRoot);}
private:// 根据AVL树的概念验证pRoot是否为有效的AVL树bool _IsAVLTree(Node* pRoot){if (pRoot == nullptr)return true;int left = _Height(pRoot->_pLeft);int right = _Height(pRoot->_pRight);int differ = right - left;if (differ >= 2 || differ <= -2)return false;if (differ != pRoot->_bf)return false;return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);}void _InOrder(Node* cur){if (cur == nullptr)return;_InOrder(cur->_pLeft);cout << cur->_data << " ";_InOrder(cur->_pRight);}size_t _Height(Node* pRoot){if (pRoot == nullptr)return 0;size_t left = _Height(pRoot->_pLeft);size_t right = _Height(pRoot->_pRight);return right > left ? right + 1 : left + 1;}// 右单旋void RotateR(Node* pParent){Node* L_Child = pParent->_pLeft;Node* LR_Child = L_Child->_pRight;//左边孩子的 右边的孩子 和parent相互连接if (LR_Child)LR_Child->_pParent = pParent;pParent->_pLeft = LR_Child;//左孩子变在上面 右边连接parent ,grandfather 相互连接Node* grandfather = pParent->_pParent;pParent->_pParent = L_Child;L_Child->_pRight = pParent;L_Child->_pParent = grandfather;if (grandfather == nullptr){_pRoot = L_Child;}else{if (grandfather->_pLeft == pParent)grandfather->_pLeft = L_Child;elsegrandfather->_pRight = L_Child;}}// 左单旋void RotateL(Node* pParent){Node* R_Child = pParent->_pRight;Node* RL_Child = R_Child->_pLeft;//if(RL_Child)RL_Child->_pParent = pParent;pParent->_pRight = RL_Child;Node* grandfather = pParent->_pParent;pParent->_pParent = R_Child;R_Child->_pLeft = pParent;R_Child->_pParent = grandfather;if (grandfather == nullptr){_pRoot = R_Child;}else{if (grandfather->_pLeft == pParent)grandfather->_pLeft = R_Child;elsegrandfather->_pRight = R_Child;}}// 右左双旋void RotateRL(Node* pParent){Node* RChild = pParent->_pRight;Node* RLChild = RChild->_pLeft;//旋转完之后再用bf来判断平衡因子int bf = RLChild->_bf;RotateR(RChild);RotateL(pParent);if (bf == 0){pParent->_bf = 0;RChild->_bf = 0;RLChild->_bf = 0;}else if (bf == 1){RLChild->_bf = 0;RChild->_bf = 0;pParent->_bf = -1;}else if (bf == -1){RLChild->_bf = 0;RChild->_bf = 1;pParent->_bf = 0;}elseassert(false);}// 左右双旋void RotateLR(Node* pParent){Node* LChild = pParent->_pLeft;Node* LRChild = LChild->_pRight;int bf = LRChild->_bf;RotateL(LChild);RotateR(pParent);if (bf == 0){LRChild->_bf = 0;pParent->_bf = 0;LChild->_bf = 0;}else if (bf == 1){LRChild->_bf = 0;LChild->_bf = -1;pParent->_bf = 0;}else if (bf == -1){LRChild->_bf = 0;LChild->_bf = 0;pParent->_bf = 1;}elseassert(false);}private:Node* _pRoot;};相关文章:

AVL树解析
目录 一. AVL的概念 二 AVL树的插入 2.1先按二叉搜索树的规则插入 2.2 AVL的重点:平衡因子更新 3.1 更新后parent的平衡因子等于0。 3.2 更新后parent的平衡因子等于1 或 -1,需要继续往上更新。 3.3 更新后parent的平衡因子等于2 或 -2,需…...
栈和队列(Java)
一.栈(Stack) 1.定义 栈是限定仅在表尾进行插入或删除操作的线性表 一般的表尾称为栈顶 表头称为栈底 栈具有“后进先出”的特点 2.对栈的模拟 栈主要具有以下功能: push(Object item):将元素item压入栈顶。 pop()&am…...

C#设计原则
文章目录 项目地址一、开放封闭原则1.1 不好的版本1.2 将BankProcess的实现改为接口1.3 修改BankStuff类和IBankClient类二、依赖倒置原则2.1 高层不应该依赖于低层模块2.1.1 不好的例子2.1.2 修改:将各个国家的歌曲抽象2.2 抽象不应该依于细节2.2.1 不同的人开不同的车(接口…...

easyfs 简易文件系统
easyfs easyfs 简易文件系统文件系统虚拟文件系统 VFS简易文件系统 easyfs磁盘布局超级块 easyfs 文件系统结构磁盘上的索引结构索引节点Inode 和 DiskInode 之间的关系举例说明读取文件的过程( /hello ) 参考文档 easyfs 简易文件系统 文件系统 常规文…...
)
【架构论文-1】面向服务架构(SOA)
【摘要】 本文以我参加公司的“生产线数字孪生”项目为例,论述了“面向服务架构设计及其应用”。该项目的目标是构建某车企的数字孪生平台,在虚拟场景中能够仿真还原真实产线的动作和节拍,实现虚实联动,从而提前规避问题ÿ…...
刚刚!更新宁德时代社招Verify测评语言理解数字推理SHL题库、网盘资料、高分答案
宁德时代社招入职的Verify测评主要分为两大块:语言理解和数字推理。语言理解部分包括阅读理解、逻辑填空和语句排序,要求在17分钟内完成30题。数字推理部分包括数字序列、数学问题解决和图表分析,同样要求在17分钟内完成18题。这些测评题目旨…...

C++笔记---智能指针
1. 什么是智能指针 1.1 RALL设计思想 RAII(Resource Acquisition Is Initialization,资源获取即初始化)是一种资源管理类的设计思想,广泛应用于C等支持对象导向编程的语言中。它的核心思想是将资源的管理与对象的生命周期紧密绑定…...

CentOS 7系统中更改YUM源为阿里云的镜像源
引言 更换阿里的镜像源可以带来诸多好处,包括提高下载速度、提升稳定性、同步更新、简化配置、节省带宽资源以及增强系统安全性等。因此,对于使用CentOS系统的用户来说,更换阿里的镜像源是一个值得考虑的选择。 1.备份yum源 mv /etc/yum.r…...

Python酷库之旅-第三方库Pandas(206)
目录 一、用法精讲 961、pandas.IntervalIndex.mid属性 961-1、语法 961-2、参数 961-3、功能 961-4、返回值 961-5、说明 961-6、用法 961-6-1、数据准备 961-6-2、代码示例 961-6-3、结果输出 962、pandas.IntervalIndex.length属性 962-1、语法 962-2、参数 …...

3.4CQU数学实验???
meshgrid 是一个用于生成网格点坐标的函数。它常用于在二维或三维空间中创建坐标网格,用于可视化和数据处理。 在二维情况下,meshgrid 函数接受两个一维数组作为输入,并返回两个二维数组,这两个数组中的元素分别表示了所有可能的…...
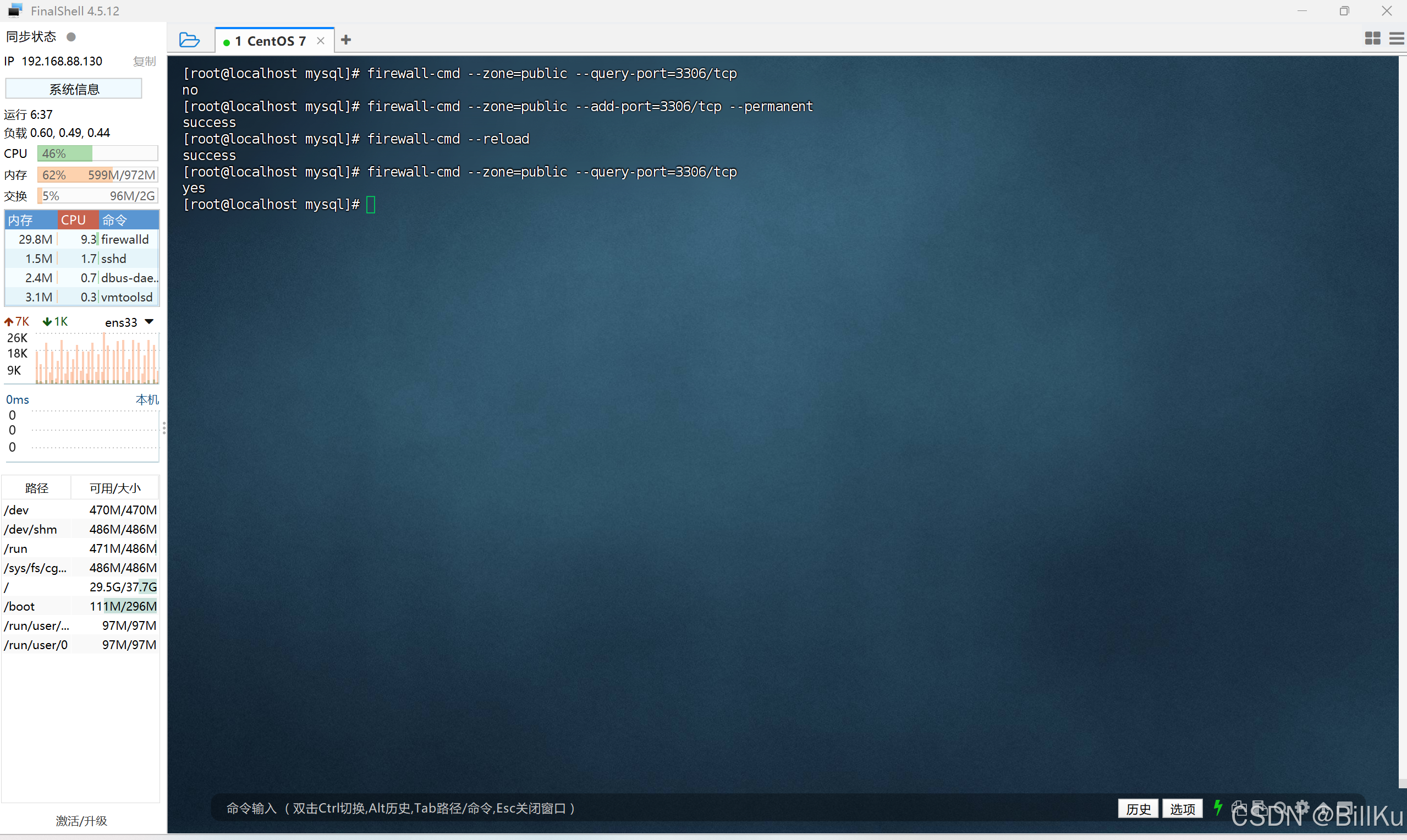
Linux(CentOS)开放端口/关闭端口
一、普通用户使用 sudo 操作,开放/关闭端口,80 1、检查端口是否开放 sudo firewall-cmd --zonepublic --query-port80/tcp 2、开放端口 sudo firewall-cmd --zonepublic --add-port80/tcp --permanent 3、重新加载(开放或关闭端口后都需…...

GreenDao适配AGP8.7+
升级配置 工具版本Android StudioLadybug 2024.2.1 Path2AGP8.7.2KPG1.8.21GGP3.3.1明细 classpath "com.android.tools.build:gradle:$agp_version"classpath "org.jetbrains.kotlin:kotlin-gradle-plugin:$kgp_version"classpath "org.greenrobot:g…...

【前端】Typescript从入门到进阶
以下是 TypeScript 的常用知识点总结,涵盖了从基础到入门的内容,并配有代码示例: 1. TypeScript 基础 1.1 安装和配置 安装 TypeScript 并初始化配置文件: npm install -g typescript tsc --init 1.2 基本类型 TypeScript 提供…...

在 RHEL 8 | CentOS Linux release 8.5.2111上安装 Zabbix 6
1. 备份YUM源文件 cd /etc/yum.repos.d/ mkdir bak mv C* ./bak/ wget -O /etc/yum.repos.d/CentOS-Linux-BaseOS.repo https://mirrors.aliyun.com/repo/Centos-vault-8.5.2111.repo yum clean all yum makecache2. 将 SELinux 设置为宽容模式,如下所示。 sudo s…...

光纤HDMI线怎么连接回音壁?
第一步:准备HDMI线、光纤线(TOSLINK线)、视频源设备、回音壁 第二步:连接HDMI线,找到视频源设备上的HDMI输出口,将HDMI线的一端插入这个接口,再把HDMI线的另一端插入回音壁的HDMI输入口。注意检…...

屏幕后期处理
1、屏幕后期处理效果 屏幕后期处理效果( Screen Post-Processing Effects)是一种在渲染管线的最后阶段应用的视觉效果,允许在场景渲染完成后对最终图像进行各种调整和效果处理,从而增强视觉体验 常见的屏幕后期处理效果有&#x…...

K8资源之endpoint资源EP资源
1 endpoint资源概述 endpoint资源在K8S中用来表s示vc与后端 Pod 之间的连接关系的对象。当创建svc时,svc根据标签是否相同或svc名字是否和ep名字相同,把svc和ip关联上。 删除svc时,会自动的删除同名的ep资源。 2 ep资源和svc的关联测试 […...

微软日志丢失事件敲响安全警钟
NEWS | 事件回顾 最近,全球最大的软件公司之一——微软,遭遇了一场罕见的日志丢失危机。据报告,从9月2日至9月19日,持续长达两周的时间里,微软的多项核心云服务,包括身份验证平台Microsoft Entra、安全信息…...

Qt生成应用程序exe
1. 将工程用MinGW编译器在release模式下编译,生成可执行文件XXX.exe,新建一个文件夹如:F:\Setup\minGW,把exe文件放到这个目录下。 2. 将该编译器的bin文件添加到PATH环境变量里:bin文件路径为:D:\Qt\Qt5.…...

C#中的HttpContent、HttpClientHandle、HttpWebRequest
C#中的HttpContent 在C#中,HttpContent 是 System.Net.Http 命名空间下的一个类,它是 HttpClient 类用来发送和接收HTTP内容的基础。HttpContent 表示HTTP请求或响应的正文内容,并且可以序列化和反序列化数据。 HttpContent 是一个抽象类&a…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
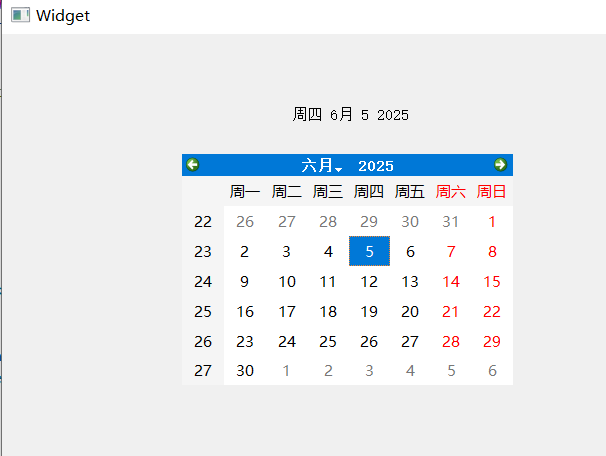
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
