动态规划 之 简单多状态 dp 问题 算法专题
一. 按摩师
按摩师
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到i位置时, 此时的最长预约时长
但是根据题目又分成两种情况:
f[i] : 选择到 i 位置的时候, nums[i] 必选, 此时的最长预约时长
g[i] : 选择到 i 位置的时候, nums[i] 不选, 此时的最长预约时长 - 状态转移方程
f[i] 如果i 位置必选, 那么f[i - 1] 位置必不选, 就等于g[i - 1] + nums[i]
g[i] 如果i位置不选, 那么g[i - 1] 位置有两种情况, 如果[i - 1] 选, 那么就=f[i - 1] ,如果[i - 1] 不选, 那么就=g[i - 1] , 但是我们要的是最长时长, 所以
- f[i] = g[i - 1] + nums[i]
- g[i] = max(f[i - 1], g[i - 1])
- 初始化
f[0] = nums[0] g[0] = 0; - 填表顺序
从左往右 两个表一起填 - 返回值
返回max(f[n], g[n])
class Solution {public int massage(int[] nums) {//1. 建表//2. 初始化//3. 填表//4. 返回值int n = nums.length;if(n == 0) return 0;int[] f = new int[n];int[] g = new int[n];f[0] = nums[0];for(int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = Math.max(f[i - 1], g[i - 1]);}return Math.max(f[n - 1], g[n - 1]);}
}
二. 打家劫舍II
打家劫舍II
分析: 通过分类讨论, 可以将环形的问题转化为线性问题
1.如果第0家偷, 那么第一家和最后一家就不能偷, 所以第二家和倒数第二家之间就可以按照正常的情况考虑
2.如果第0家不偷, 那么剩下的都可以正常进行了
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到i位置时, 此时偷的最大金额
但是根据题目又分成两种情况:
f[i] : 选择到 i 位置的时候, nums[i] 必选, 此时偷的最大金额
g[i] : 选择到 i 位置的时候, nums[i] 不选, 此时偷的最大金额 - 状态转移方程
f[i] 如果i 位置必选, 那么f[i - 1] 位置必不选, 就等于g[i - 1] + nums[i]
g[i] 如果i位置不选, 那么g[i - 1] 位置有两种情况, 如果[i - 1] 选, 那么就=f[i - 1] ,如果[i - 1] 不选, 那么就=g[i - 1] , 但是我们要的是偷的最大金额, 所以
- f[i] = g[i - 1] + nums[i]
- g[i] = max(f[i - 1], g[i - 1])
- 初始化
f[0] = nums[0] g[0] = 0; - 填表顺序
从左往右 两个表一起填 - 返回值
返回第0家偷和不偷的最大值
class Solution {int[] f;int[] g;int[] nums;public int rob(int[] _nums) {// 1. 建表// 2. 初始化// 3. 填表// 4. 返回值nums = _nums;int n = _nums.length;int x = rob1(2, n - 2) + nums[0];int y = rob1(1, n - 1);return Math.max(x, y);}public int rob1(int left, int right) {if(left > right) return 0;int n = nums.length;f = new int[n];g = new int[n];f[left] = nums[left];for (int i = left; i <= right; i++) {f[i] = g[i - 1] + nums[i];g[i] = Math.max(g[i - 1], f[i - 1]);}return Math.max(f[right], g[right]);}}
三. 删除并获得点数
删除并获得点数
分析: 由于是删除大于或和小于的数, 也就是说相邻的数是不能再选的, 那么和打家劫舍问题是类似的
但是这些数并不是相邻的并且无序, 所以我们需要重新定义一个数组arr来存储
点数代表下标, 对应的值就是该点数的总和
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到i位置时, 此时获得的最大点数
但是根据题目又分成两种情况:
f[i] : 选择到 i 位置的时候, nums[i] 必选, 此时获得的最大点数
g[i] : 选择到 i 位置的时候, nums[i] 不选, 此时获得的最大点数 - 状态转移方程
f[i] 如果i 位置必选, 那么f[i - 1] 位置必不选, 就等于g[i - 1] + arr[i]
g[i] 如果i位置不选, 那么g[i - 1] 位置有两种情况, 如果[i - 1] 选, 那么就=f[i - 1] ,如果[i - 1] 不选, 那么就=g[i - 1] , 但是我们要的是获得的最大点数, 所以
- f[i] = g[i - 1] + nums[i]
- g[i] = max(f[i - 1], g[i - 1])
- 初始化
f[0] = arr[0] g[0] = 0; - 填表顺序
从左往右 两个表一起填 - 返回值
返回max(f[n - 1], g[n - 1])
class Solution {public int deleteAndEarn(int[] nums) {//预处理int n = 10001;int[] arr = new int[n];for(int x: nums) arr[x] += x;//建表//初始化//填表//返回值int[] f = new int[n];int[] g = new int[n];f[0] = arr[0];for(int i = 1; i < n; i++){f[i] = g[i - 1] + arr[i];g[i] = Math.max(f[i - 1], g[i - 1]);}return Math.max(f[n - 1], g[n - 1]);}
}
四, 粉刷房子
粉刷房子
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到i位置时, 此时粉刷的最小花费
但是根据题目又分成两种情况:
如果第i个房子, 粉刷的是红色的, 那么前一个房子只能是蓝色或绿色, 同理其他情况
所以dp可以弄成二维数组, dp[i][j] 表示最小费用, j表示颜色 0红色,1蓝色,2绿色 - 状态转移方程
1.如果i选择红色, dp[i][0], 那么dp[i - 1]只能选择[1][2], 要的是最小花费, 所以
- dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0]
2.如果i选择蓝色, dp[i][0], 那么dp[i - 1]只能选择[1][2], 要的是最小花费, 所以
- dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1]
3.如果i选择红色, dp[i][0], 那么dp[i - 1]只能选择[1][2], 要的是最小花费, 所以
- dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2]
- 初始化
本道题初始化较为复杂, 所以使用虚拟节点来帮助我们初始化, 要注意两个注意事项: 初始化与对应关系
最开始是0的位置最小花费应该初始化为0, 因为还没有花费 - 填表顺序
从左往右 两个表一起填 - 返回值
返回min(dp[n][0], dp[n][1], dp[n][2])
class Solution {public int minCost(int[][] costs) {int n = costs.length;int[][] dp = new int[n + 1][3];for(int i = 1; i <= n; i++){//i遍历的是行dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2];}return Math.min(Math.min(dp[n][0], dp[n][1]), dp[n][2]);}
}
五. 买卖股票的最佳时机含冷冻期
买卖股票的最佳时机含冷冻期
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到第i天位置时, 此时的最大利润
但是到第i天又分成三种情况:
可能处于"买入"状态, "可交易"状态, "冷冻期"状态
所以用二维数组[i][j]状态表示 0"买入"状态, 1"可交易"状态, 2"冷冻期"状态 - 状态转移方程
1.如果处于"买入"状态, 那么第i - 1天, 可能处于"买入"状态(i - 1天买完后第i天没卖, 等于啥也没干), 可能处于"可交易"状态(i - 1天不是冷冻期, 可以进行购买), 此时是需要-价格, 进行购买, 由于要最大利润, 对两次状态的结果取最大值
- dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
2.如果处于"可交易"状态, 那么第i - 1天, 可能处于"可交易"状态(i - 1天之前就卖了, 第i天还没买, 等于啥也没干), 可能处于"冷冻期"状态(i - 1天卖了, 第i天还没买, 等于啥也没干), 由于要最大利润, 对两次状态的结果取最大值
- dp[i][1] = max(dp[i - 1][1], dp[i - 1][2])
3.如果处于"冷冻期"状态, 那么第i - 1天, 可能处于"买入"状态(i - 1天买了, 第i天卖了), , 此时是需要+价格, 进行购买,
- dp[i][2] =dp[i - 1][0] + price[i]
- 初始化
只需对0位置进行初始化
dp[0][0] 说明买了股票, 利润为-prices[0]
dp[0][1] 说明可以买, 利润为0
dp[0][2] 说明冷冻期, 利润为0 - 填表顺序
从左往右 三个表一起填 - 返回值
返回max(dp[n - 1][0], dp[n - 1][1], dp[n - 1][2])
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][3];dp[0][0] = -prices[0];for(int i = 1; i < n; i++){dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] =dp[i - 1][0] + prices[i];}return Math.max(Math.max(dp[n - 1][0], dp[n - 1][1]), dp[n - 1][2]);}
}
六. 买卖股票的最佳时机含手续费
买卖股票的最佳时机含手续费
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到第i天位置时, 此时的最大利润 - 状态转移方程
第i天位置时, 有两种情况
1.可能处于"买入"状态
那么i - 1 位置可能是"买入"状态(啥也不干), 可能是"可交易"状态(买股票)
f[i] = max(f[i - 1], g[i - 1] - p[i])
2.可能处于"可交易"状态
那么i - 1 位置可能是"买入"状态(卖股票, 再加上手续费), 可能是"可交易"状态(啥也不干)
g[i] = max(f[i - 1] + p[i] - fee, g[i - 1]) - 初始化
f[0] = -p[0] g[0] = 0 - 填表顺序
从左往右 两个表一起填 - 返回值
max(g[n - 1], f[n - 1])
class Solution {public int maxProfit(int[] prices, int fee) {int n = prices.length;int[] f = new int[n];int[] g = new int[n];f[0] = -prices[0];for(int i = 1; i < n; i++){f[i] = Math.max(f[i - 1], g[i - 1] - prices[i]);g[i] = Math.max(f[i - 1] + prices[i] - fee, g[i - 1]);}return Math.max(g[n - 1], f[n - 1]);}
}
七. 买卖股票的最佳时机III
买卖股票的最佳时机III
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到第i天结束之后, 此时的最大利润
第i天位置时, 有两种情况, "买入"状态 和 "可交易"状态, 但是还要记录交易次数, 所以我们要使用二维数组 - 状态转移方程
1.第i天可能处于"买入"状态, 此时完成了j次交易, i为最大利润
那么i - 1 位置可能是"买入"状态(啥也不干), 可能是"可交易"状态(买股票)
f[i][j] = max(f[i - 1][j], g[i - 1][j] - p[i])
2.第i天可能处于"可交易"状态, 此时完成了j次交易, i为最大利润
那么i - 1 位置可能是"买入"状态(卖股票, 交易次数 + 1), 可能是"可交易"状态(啥也不干)
g[i][j] = max(f[i - 1][j - 1] + p[i], g[i - 1][j]) - 初始化
f需要初始化第一行, g需要初始化第一行第一列
所以我们可以修改一下状态转移方程, 只初始化第一行即可
g[i][j] = g[i - 1][j];
if(j - 1 >= 0) max(f[i - 1][j - 1] + p[i], g[i][j])
f[0][0] = -p[0] 第0天不可能完成多笔交易, 所以第一行其余填-0x3f3f3f3f (INT_MIN的一半, 不初始化为INT_MIN, 防止溢出
g[0][0] = 0 第一行其余填-0x3f3f3f3f
4. 填表顺序
从左往右 从上往下 两个表一起填
5. 返回值
返回可交易表最后一行的最大值
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int INF = 0x3f3f3f3f;int[][] f = new int[n][3];int[][] g = new int[n][3];for(int j = 0; j < 3; j++){f[0][j] = g[0][j] = -INF;}f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1; i < n; i++){for(int j = 0; j < 3; j++){f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j - 1 >= 0) g[i][j] = Math.max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for(int j = 0; j < 3; j++){ret = Math.max(ret, g[n - 1][j]);}return ret;}
}
八. 买卖股票的最佳时机IV
买卖股票的最佳时机IV
- 状态表示
根据经验 + 题目要求
dp[i] 表示: 选择到第i天结束之后, 此时的最大利润
第i天位置时, 有两种情况, "买入"状态 和 "可交易"状态, 但是还要记录交易次数, 所以我们要使用二维数组 - 状态转移方程
1.第i天可能处于"买入"状态, 此时完成了j次交易, i为最大利润
那么i - 1 位置可能是"买入"状态(啥也不干), 可能是"可交易"状态(买股票)
f[i][j] = max(f[i - 1][j], g[i - 1][j] - p[i])
2.第i天可能处于"可交易"状态, 此时完成了j次交易, i为最大利润
那么i - 1 位置可能是"买入"状态(卖股票, 交易次数 + 1), 可能是"可交易"状态(啥也不干)
g[i][j] = max(f[i - 1][j - 1] + p[i], g[i - 1][j]) - 初始化
f需要初始化第一行, g需要初始化第一行第一列
所以我们可以修改一下状态转移方程, 只初始化第一行即可
g[i][j] = g[i - 1][j];
if(j - 1 >= 0) max(f[i - 1][j - 1] + p[i], g[i][j])
f[0][0] = -p[0] 第0天不可能完成多笔交易, 所以第一行其余填-0x3f3f3f3f (INT_MIN的一半, 不初始化为INT_MIN, 防止溢出
g[0][0] = 0 第一行其余填-0x3f3f3f3f
4. 填表顺序
从左往右 从上往下 两个表一起填
5. 返回值
返回可交易表最后一行的最大值
class Solution {public int maxProfit(int k, int[] prices) {int n = prices.length;k = Math.min(k, n / 2);int INF = 0x3f3f3f3f;int[][] f = new int[n][k + 1];int[][] g = new int[n][k + 1];for(int j = 0; j <= k; j++){f[0][j] = g[0][j] = -INF;}f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1; i < n; i++){for(int j = 0; j <= k; j++){f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j - 1 >= 0) g[i][j] = Math.max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for(int j = 0; j <= k; j++){ret = Math.max(ret, g[n - 1][j]);}return ret;}
}
相关文章:

动态规划 之 简单多状态 dp 问题 算法专题
一. 按摩师 按摩师 状态表示 根据经验 题目要求 dp[i] 表示: 选择到i位置时, 此时的最长预约时长 但是根据题目又分成两种情况: f[i] : 选择到 i 位置的时候, nums[i] 必选, 此时的最长预约时长 g[i] : 选择到 i 位置的时候, nums[i] 不选, 此时的最长预约时长状态转移方程 …...

qt QPixmapCache详解
1、概述 QPixmapCache是Qt框架中提供的一个功能强大的图像缓存管理工具类。它允许开发者在全局范围内缓存QPixmap对象,从而有效减少图像的重复加载,提高图像加载和显示的效率。这对于需要频繁加载和显示图像的用户界面应用来说尤为重要,能够…...

Redis中的持久化
什么是 Redis 持久化? Redis 是一个内存数据库,也就是说它主要把数据存储在内存中,这样可以实现非常高的读写速度。通常,内存数据库是非常快速且高效的,但它也有一个很大的问题:数据丢失的风险。因为当 Red…...

Unity 如何优雅的限定文本长度, 包含对特殊字符,汉字,数字的处理。实际的案例包括 用户昵称
常规限定文本长度 ( 通过 UntiyEngine.UI.Inputfiled 附带的长度限定 ) 痛点1 无法对中文,数字,英文进行识别,同样数量的汉字和同样数量的英文像素长度是不一样的,当我们限定固定长度后,在界面上的排版不够美观 痛点2…...
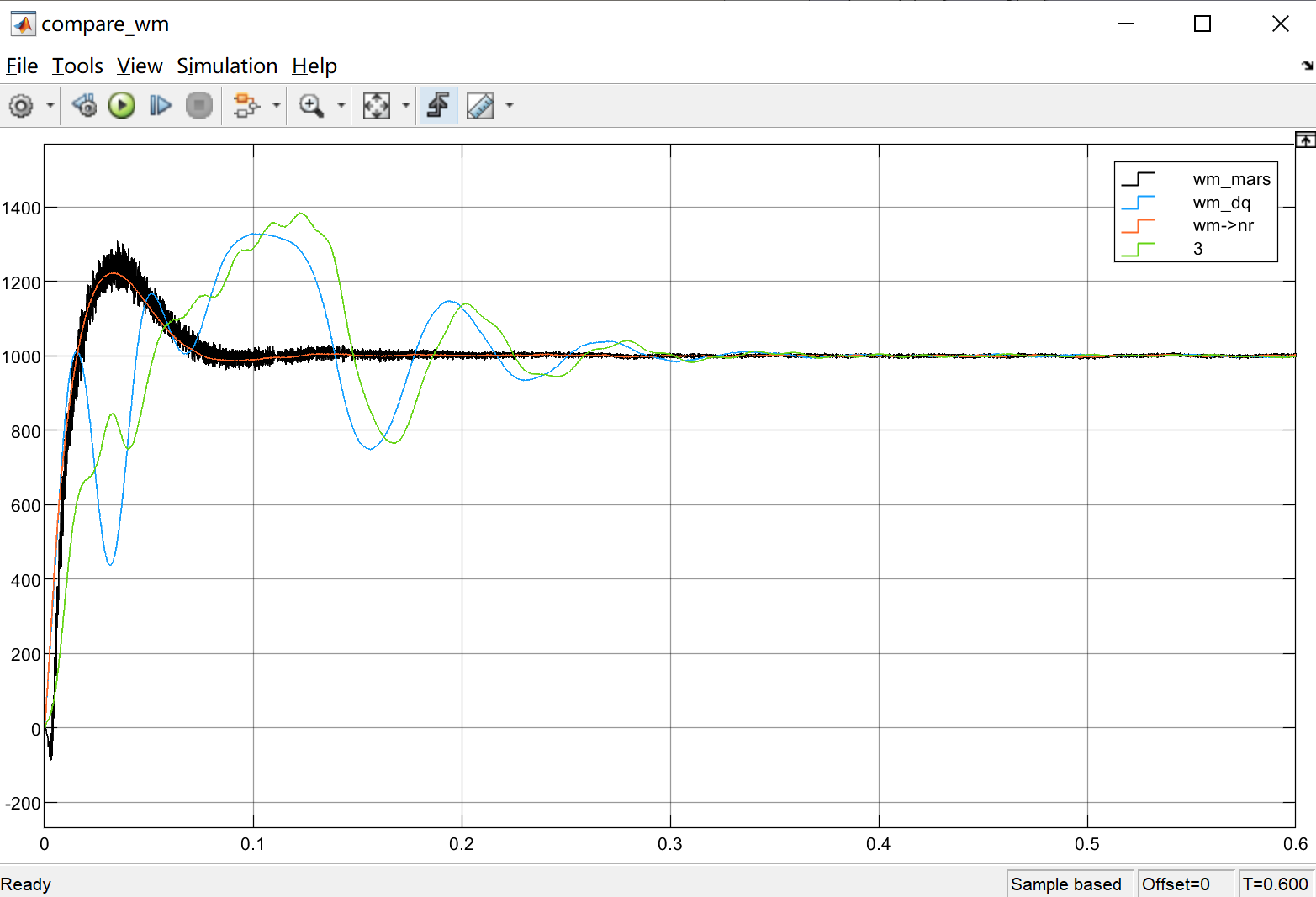
SMO+PLL滑膜观测器、MARS模型参考自适应观测器simulink仿真
模型内容介绍: (1)SMOPLL滑膜观测器通过SMO估计电机的转速和位置信息,并利用PLL技术对这些信息进行跟踪和校正,以实现高精度的电机控制; (2)MARS是一种基于模型参考自适应控制理论…...
找出单独的数)
例题解析:利用异或运算(XOR)找出单独的数
异或运算(XOR) 异或运算是一种位运算,通常用符号 ^ 表示。它的运算规则如下: 如果两个二进制位相同,结果为 0。如果两个二进制位不同,结果为 1。 具体来说,对于两个二进制位 a 和 bÿ…...
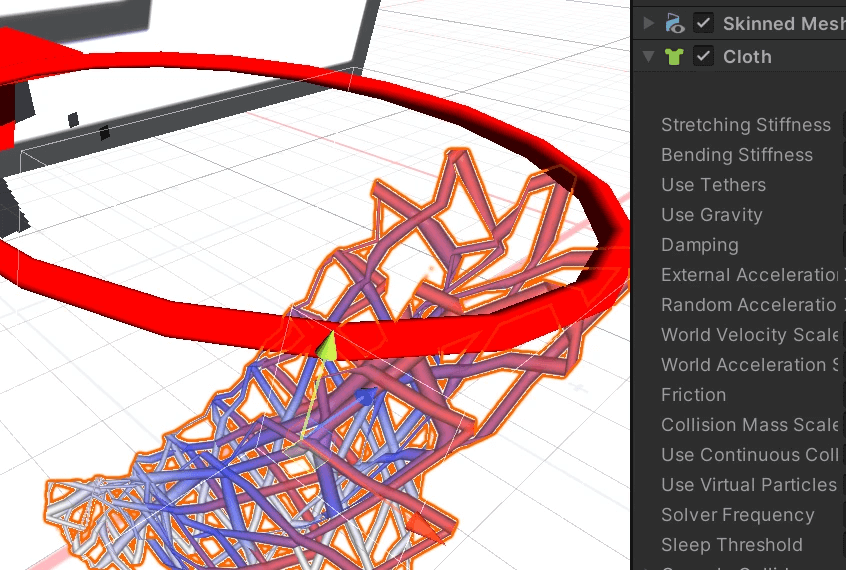
如何处理微信小程序大量未捕获的异常
1)如何处理微信小程序大量未捕获的异常 2)如何关闭代码创建的纹理的读写,或者创建不带读写的图片 3)回收带有贴图和Collider的Mesh,如何正确用对象池维护 4)Cloth组件使用在一个篮筐上,运行后篮…...

C#-StringBuilder
string:特殊的引用 每次重新赋值或者拼接时会分配新的内存空间,如果一个字符串经常改变会非常浪费空间。 StringBuilder:C#提供的一个用于处理字符串的公共类 修改字符串而不创建新的对象,需要频繁修改和拼接的字符串可以使用它…...

SQLI LABS | Less-39 GET-Stacked Query Injection-Intiger Based
关注这个靶场的其它相关笔记:SQLI LABS —— 靶场笔记合集-CSDN博客 0x01:过关流程 输入下面的链接进入靶场(如果你的地址和我不一样,按照你本地的环境来): http://localhost/sqli-labs/Less-39/ 本关是堆…...

linux安装zookeeper和kafka集群
linux安装zookeeper和kafka集群 一、Zookeeper集群部署安装zookeeper1. 下载2. 上传, 解压3. 配置 Zookeeper 节点4. 创建 myid 文件5. 启动参数更改6. sh文件授权7. 启动集群8. 防火墙开启端口 验证集群 二、kafka集群安装安装Kafka1. 下载Kafka安装包2. 上传到服务器…...

洞悉 Linux 系统运行细节,使用 atop 监测和回看系统负载状态
Linux系统的资源使用情况,你可以通过使用命令如free、top和netstat来实时监控内存、CPU及端口的使用状态。对于需要追踪历史资源消耗动态的场景,atop命令则能有效帮助用户查看过去的系统负载情况。 本篇教程的灵感源自一位小伙伴的真实经历:…...
“双十一”电商狂欢进行时,在AI的加持下看网易云信IM、RTC如何助力商家!
作为一年一度的消费盛会,2024年“双十一”购物狂欢节早已拉开帷幕。蹲守直播间、在主播热情介绍中点开链接并加购,也已成为大多数人打开“双11”的重要方式。然而,在这火热的购物氛围背后,主播频频“翻车”、优质主播稀缺、客服响…...

Python调用企业微信的扫一扫
在企业微信里面新建了一个应用,指向了搭建服务器上Django写的web应用。 web应用需要使用扫描二维码的功能,就使用了大家都评价效果好的微信的扫一扫,事实也证明微信的扫一扫很好,但实现这个功能还是花了自己不少时间,很…...

速盾:CDN和OBS能共用流量包吗?
CDN和OBS是两种不同的云服务,它们在内容分发和存储方面有着不同的功能和优势。虽然它们都可以用于提供高效的内容分发和存储服务,但是它们的流量包是不能共用的。 CDN,即内容分发网络,是一种通过将内容存储在全球分布的服务器上&…...

第8章 利用CSS制作导航菜单
8.1 水平顶部导航栏 水平莱单导航栏是网站设计中应用范围最广的导航设计,一般放置在页面的顶部。水平 导航适用性强,几乎所有类型的网站都可以使用,设计难度较低。 如果导航过于普通,无法容纳复杂的信息结构,就需要在…...

C# 集合与泛型
文章目录 前言1.什么是集合?2.非泛型集合(了解即可)2.1常见的非泛型集合 3.泛型的概念4.常用的泛型集合4.1 List < T > <T> <T>4.2 Dictionary<TKey, TValue>4.3 Queue < T > <T> <T>4.4 S t a c…...

el-date-picker 设置开始时间和结束时间
<el-date-picker v-model"ruleForm.RECORDDATE" type"date" placeholder"日期" format"YYYY/M/D" value-format"YYYY/M/D" style"width: 100%;" :disabled-date"publishDateAfter" > </el-dat…...

【Docker】 常用命令
文章目录 介绍Docker和容器化技术什么是Docker?Docker的优势和应用场景Docker的应用场景包括但不限于: 安装和配置Docker安装Docker引擎配置Docker环境 Docker镜像命令搜索镜像拉取镜像查看本地镜像删除本地镜像 Docker容器命令创建容器启动容器停止容器…...

docker compose - 设置名字
只使用 docker compose up 启动容器,默认名字为当前文件夹的名字 设置 project-name,docker 客户端会显示设置的名字,方便区分 docker compose --project-name webtest up错误: docker compose up --project-name webtest 效果…...

工业拍卖平台、信息发布、租赁商城平台系统适用于全行业解决方案。
工业拍卖平台系统是为工业领域的资产交易、设备处置等提供线上拍卖服务的数字化平台。 主要功能: 拍卖信息发布:平台会展示待拍卖的工业资产详细信息,包括设备的名称、型号、规格、使用年限、生产厂家等基本信息,以及资产的图片…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
