算法基础 -- 红黑树原理与插入伪代码
红黑树原理与插入伪代码
红黑树的原理
红黑树是一种自平衡的二叉搜索树,通过对节点的颜色(红色或黑色)以及结构的约束条件来保持树的平衡。红黑树的原理可以通过以下五个特性描述:
- 节点是红色或黑色。
- 根节点必须是黑色。
- 所有叶节点(即
NULL节点)都是黑色的。 - 红色节点的子节点必须是黑色,即红色节点不能有红色的父节点或子节点(无双红特性)。
- 从任一节点到其所有后代叶节点的所有路径上,必须包含相同数目的黑色节点。
这些特性使红黑树能够在最坏情况下保证查找、插入和删除操作的时间复杂度为 O(log n),从而保持较好的性能。
红黑树的插入操作
红黑树的插入操作相对复杂,因为在每次插入新节点时,可能会破坏树的平衡。因此,需要进行颜色修正和旋转操作来重新平衡树。插入过程可以分为两个阶段:
- 插入节点:将新节点插入到树中,类似于普通的二叉搜索树插入。
- 修复树:修复因插入而可能破坏的红黑树特性。
插入节点的伪代码
function RB_INSERT(tree, value):new_node = Node(value)new_node.color = RED # 新插入的节点初始为红色new_node.left = NULL # 左子节点为空new_node.right = NULL # 右子节点为空# 1. 查找插入位置current = tree.rootparent = NULLwhile current is not NULL:parent = currentif new_node.value < current.value:current = current.leftelse:current = current.right# 2. 插入节点并设置父节点new_node.parent = parentif parent is NULL:tree.root = new_node # 树为空,新节点为根else if new_node.value < parent.value:parent.left = new_node # 新节点为左子节点else:parent.right = new_node # 新节点为右子节点# 3. 修复红黑树的平衡性RB_INSERT_FIXUP(tree, new_node)
修复树的伪代码
插入后,红黑树的性质可能被破坏,特别是双红问题(即父节点和子节点都是红色)。需要通过旋转和重新着色来修复树的平衡。
function RB_INSERT_FIXUP(tree, node):while node.parent is not NULL and node.parent.color == RED:if node.parent == node.parent.parent.left: # 父节点是祖父的左子节点uncle = node.parent.parent.right # 叔叔节点if uncle is not NULL and uncle.color == RED: # 情况 1:叔叔节点是红色node.parent.color = BLACK # 将父节点设为黑色uncle.color = BLACK # 将叔叔节点设为黑色node.parent.parent.color = RED # 将祖父节点设为红色node = node.parent.parent # 将祖父节点作为新的当前节点继续检查else:if node == node.parent.right: # 情况 2:叔叔是黑色,且当前节点是右子节点node = node.parentLEFT_ROTATE(tree, node) # 左旋父节点node.parent.color = BLACK # 情况 3:叔叔是黑色,且当前节点是左子节点node.parent.parent.color = REDRIGHT_ROTATE(tree, node.parent.parent) # 右旋祖父节点else: # 父节点是祖父的右子节点(对称情况)uncle = node.parent.parent.left # 叔叔节点if uncle is not NULL and uncle.color == RED: # 情况 1:叔叔节点是红色node.parent.color = BLACKuncle.color = BLACKnode.parent.parent.color = REDnode = node.parent.parentelse:if node == node.parent.left: # 情况 2:叔叔是黑色,且当前节点是左子节点node = node.parentRIGHT_ROTATE(tree, node) # 右旋父节点node.parent.color = BLACK # 情况 3:叔叔是黑色,且当前节点是右子节点node.parent.parent.color = REDLEFT_ROTATE(tree, node.parent.parent) # 左旋祖父节点# 保证根节点为黑色tree.root.color = BLACK
左旋和右旋的伪代码
红黑树的平衡性是通过旋转来实现的。左旋和右旋操作用于在插入或删除节点时调整树的结构。
左旋的伪代码
function LEFT_ROTATE(tree, node):right_child = node.right # 当前节点的右子节点node.right = right_child.left # 右子节点的左子树变为当前节点的右子树if right_child.left is not NULL:right_child.left.parent = noderight_child.parent = node.parent # 右子节点的父节点更新为当前节点的父节点if node.parent is NULL:tree.root = right_child # 当前节点是根节点,更新根节点else if node == node.parent.left:node.parent.left = right_childelse:node.parent.right = right_childright_child.left = node # 当前节点变为右子节点的左子节点node.parent = right_child
右旋的伪代码
function RIGHT_ROTATE(tree, node):left_child = node.left # 当前节点的左子节点node.left = left_child.right # 左子节点的右子树变为当前节点的左子树if left_child.right is not NULL:left_child.right.parent = nodeleft_child.parent = node.parent # 左子节点的父节点更新为当前节点的父节点if node.parent is NULL:tree.root = left_child # 当前节点是根节点,更新根节点else if node == node.parent.left:node.parent.left = left_childelse:node.parent.right = left_childleft_child.right = node # 当前节点变为左子节点的右子节点node.parent = left_child
总结
红黑树的插入操作通过节点插入、颜色修正以及旋转操作来保持树的平衡,确保了最坏情况下的时间复杂度为 O(log n)。插入伪代码的核心在于将新节点插入树中,然后通过颜色修正和旋转操作来保持红黑树的平衡特性。这使得红黑树能够在多次插入和删除操作后,依旧保持良好的查找性能。
相关文章:

算法基础 -- 红黑树原理与插入伪代码
红黑树原理与插入伪代码 红黑树的原理 红黑树是一种自平衡的二叉搜索树,通过对节点的颜色(红色或黑色)以及结构的约束条件来保持树的平衡。红黑树的原理可以通过以下五个特性描述: 节点是红色或黑色。根节点必须是黑色。所有叶…...

力扣 LeetCode 27. 移除元素(Day1:数组)
解题思路: 注意:数组只能覆盖,不能删除 erase方法的复杂度为O( n )而不是O( 1 ),因为需要把删除后后面的数组向前移动 方法一:双层for循环暴力 方法二:快慢指针 fast表示新数组的元素 slow表示新数组元…...

微服务链路追踪skywalking安装
SkyWalking是一个开源的分布式追踪系统,主要用于监控和分析微服务架构下的应用性能。 它提供了分布式追踪、服务网格遥测分析、度量聚合和可视化一体化解决方案,特别适用于微服务、云原生架构和基于容器的环境(如Docker、K8s、Mesos&…...
)
mqtt学习笔记(一)
以解决问题方式逐步学习探索 mqtt使用场景mqtt可能缺点mqtt学习疑问探索1、mqtt主题发布过的历史消息,全新连接的client能消费到吗?2、mqtt的client掉线如何重连,重连后订阅的topic配置还在不?3、mqtt的client掉线重连后ÿ…...

Kafka Eagle 安装教程
目录 前言 一、安装前的准备 1. 系统要求 2. 安装 JDK 3. 安装 Kafka 和 Zookeeper 4. MySQL 环境准备 二、下载并安装 Kafka Eagle 三、配置 Kafka Eagle 1. 编辑配置文件 2. 配置 Kafka 和 Zookeeper 信息 四、启动 Kafka Eagle 五、访问 Kafka Eagle 六、测试功…...

Ajax 获取进度和中断请求
HTML加入一些内容方便看效果和做交互: <div><p>当前传输进度:<span id"progress">0%</span></p><button id"send">发送</button><button id"btn">中断</button> …...

实验5:网络设备发现、管理和维护
实验5:网络设备发现、管理和维护 实验目的及要求: 通过实验,掌握Cisco 路由器和交换机的IOS配置管理。自动从NTP服务器获取时间信息。能够利用TFTP服务器实现路由器和交换机配置文件的备份和恢复。同时验证CDP协议和LLDP协议的网络参数。完…...

kafka 生产经验——数据积压(消费者如何提高吞吐量)
bit --> byte --> kb -->mb -->gb --> tb --> pb --> eb -> zb -->yb...
介绍)
对等同步身份认证(Simultaneous Authentication of Equals,简称SAE)介绍
对等同步身份认证(Simultaneous Authentication of Equals,简称SAE)介绍 对等同步身份认证(Simultaneous Authentication of Equals,简称SAE)是一种基于密码的身份验证方法,用于安全地交换密钥…...
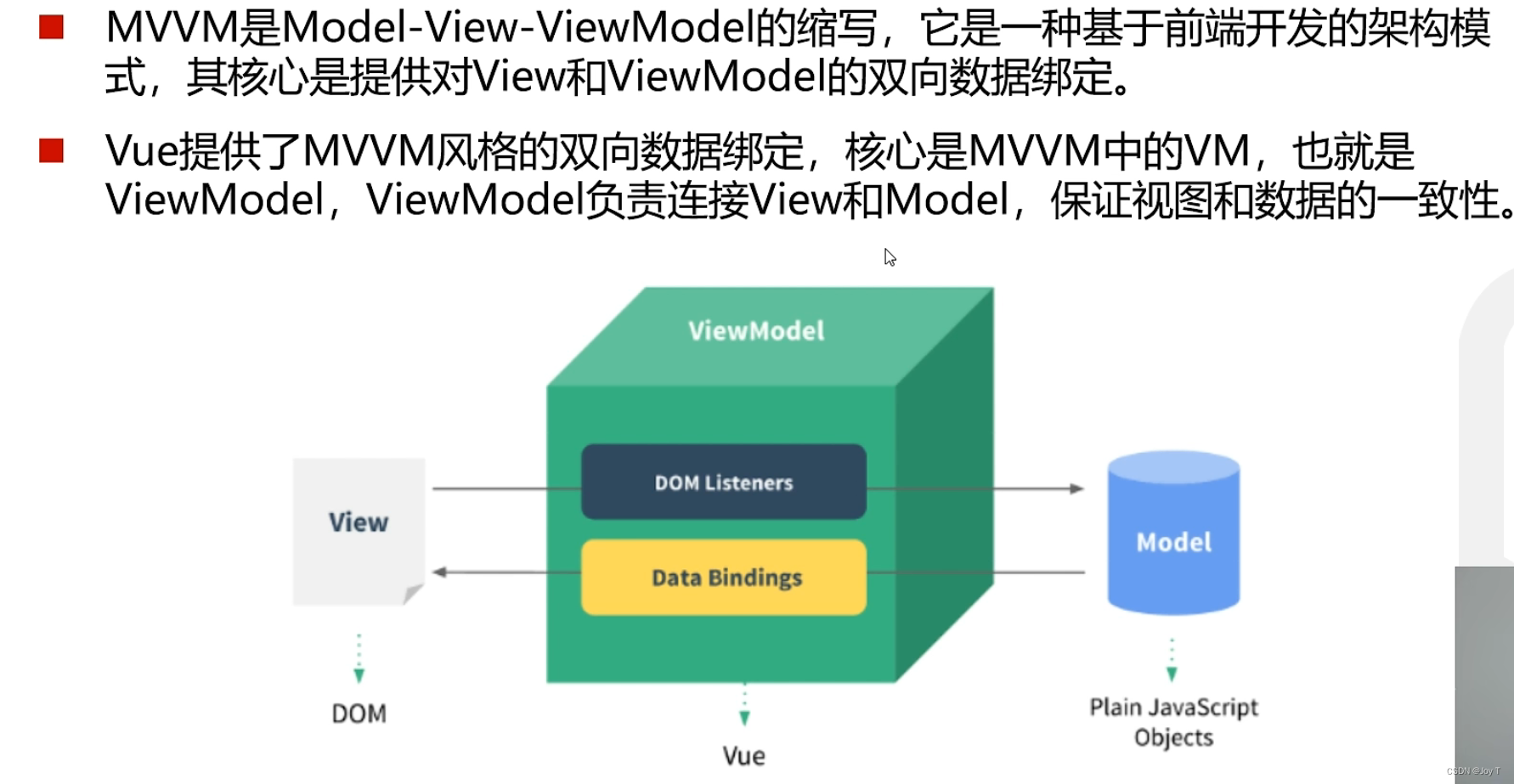
Ajax 与 Vue 框架应用点——随笔谈
老式 在老式的技术中,一个网页通常由前端工程师直接使用 HTML、CSS、JavaScript 编写而成 这种方式的优点很明显:简单粗暴,方便工程师以简单的思维完成工作 当然,缺点也很明显,包括但不限于: 直接原生开发…...

The Internals of PostgreSQL 翻译版 持续更新...
为了方便自己快速学习,整理了翻译版本,目前翻译的还不完善,后续会边学习边完善。 文档用于自己快速参考,会持续修正,能力有限,无法确保正确!!! 《The Internals of PostgreSQL 》 不是 《 PostgreSQL14 Internals 》…...

redis 原理篇 31 redis内存回收 内存淘汰策略
哦哦, 内存满了咋搞 就算过期key 删除,还是不够用, 这种问题没办法,只能了解一下啥解决方案了, 内存是有限的,一直存,肯定会满,这时,咋处理? 首先ÿ…...

微信小程序——实现二维码扫描功能(含代码)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

【go从零单排】HTTP客户端和服务端
🌈Don’t worry , just coding! 内耗与overthinking只会削弱你的精力,虚度你的光阴,每天迈出一小步,回头时发现已经走了很远。 📗概念 在 Go 语言中,net/http 包提供了强大的 HTTP 客户端和服务器功能。 &…...

Android 配置默认输入法
1.背景 最近有个国内的项目,预制了输入法apk,但是无法调出软键盘。原因是没有配置默认输入法,本文主要记录下如何配置默认输入法。 2.代码设置 设置默认输入法需要配置Settings.Secure.ENABLED_INPUT_METHODS和Settings.Secure.DEFAULT_IN…...
)
交易术语汇总(Technical Trading Dictionary)
Arbitrage (套利) --- 一种利用交易所之间的差价获利的方法。 Accumulation (累积) --- 在一种资产中建立头寸的过程。 Ask/Bid (询价/竞价) --- 卖出订单是询价(Ask),买入订单是出价(Bid)。 ATH(历史最高价) --- All-time high 全时高。 Bearish MS…...

【Docker】Docker基础及docker-compose
一、Docker下载 更新yum包 yum update 安装需要的软件包( yum-util 提供yum-config-manager功能,后两个是devicemapper驱动依赖) yum install -y yum-utils device-mapper-persistent-data lvm2 设置stable镜像仓库(使用阿里…...

从零开始的 Hugging Face 项目:我的首个在线 SQL 查询工具之旅20241111
从零开始的 Hugging Face 项目:我的首个在线 SQL 查询工具之旅 作为一名 AI 初学者,我最近完成了一个意义非凡的项目:在 Hugging Face Spaces 上构建了一个简单却实用的在线 SQL 查询工具。这个项目不仅让我了解了 Hugging Face 平台的核心功…...
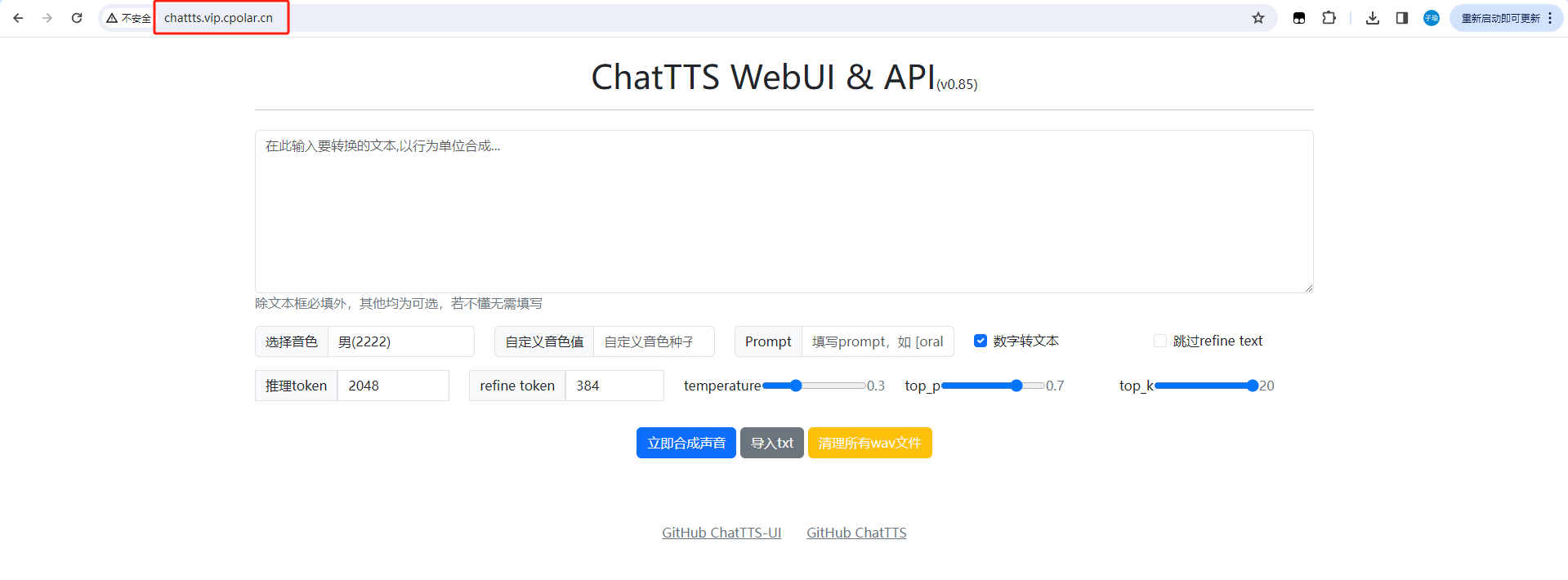
让AI为你发声!Windows电脑快速部署ChatTTS文本转语音神器
文章目录 前言1. 下载运行ChatTTS模型2. 安装Cpolar工具3. 实现公网访问4. 配置ChatTTS固定公网地址 前言 嘿,朋友们!今天我们来聊聊如何在Windows系统上快速搭建ChatTTS,一个超酷的开源文本转语音项目。更棒的是,我们还可以用Cp…...

【AI换脸整合包及教程】FaceFusion 3.0.0:AI换脸技术的革新之旅
在人工智能技术的飞速发展中,AI换脸技术成为了近年来备受瞩目的焦点之一。FaceFusion 3.0.0,作为这一领域的最新力作,不仅继承了前代产品的优点,还在功能和用户体验上进行了全面升级和优化,为用户带来了前所未有的换脸…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
