【数据结构与算法】单调队列 | 单调栈
🌠作者:@阿亮joy.
🎆专栏:《数据结构与算法要啸着学》
🎇座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根
目录
- 👉滑动窗口的最大值👈
- 👉单调队列的实现👈
- 👉单调栈的实现👈
- 数组无重复值版本的单调栈
- 每日温度
- 数组有重复值版本的单调栈
- 指标A的最大值
- 👉总结👈
👉滑动窗口的最大值👈
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
这是一道可以使用单调队列的经典题。如果使用暴力方法的话,就是遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是 O(k × N) 的算法。而使用单调队列来解这道题目,时间复杂度是 O(N)。
那什么是单调队列呢?单调队列是具有单调性的队列,其里面存储的元素单增或者单减。单调队列需要保证的一个功能就是:每次插入元素或者删除元素,其队头的元素都是最大值或者最小值。为了实现这个功能,我们需要用双端队列 deque 来做适配器。
为了说明单调队列的功能,假设数组中的元素是 6 4 2 5 3。注:一下过程假设队头数据是最大值,队头数据是最小值同理。窗口的右边界往右移动,则说明要插入新数据。如果新插入的数据比队尾的数据小,则直接将数据从队尾插入;而如果新插入的数据对队尾的数据大,则需要将队尾数据弹出直至队尾数据大于新插入的数据或队列为空。窗口的左边界往右移动,则说明可能要弹出队头数据。如果从窗口出来的数据就是队头数据,则说明队头数据已过期,需要将队头数据弹出;而如果从窗口出来的数据不是队头数据,则不需要弹出队头数据。

为什么单调队列就能够保证它里面存储的就是窗口内的最大值呢?其实它是通过新加入的值是否会比前面的值大,如果是,就将前面的元素从尾部弹出。因为新加入的元素肯定比它们晚离开窗口,而且值有比它们大,所以只需要保留新加入元素就可以保证窗口内的最大值在队列中。
那如何估计单调队列解决滑动窗口最大值的时间复杂度呢?数组中的每个元素最多进队列一次,出队列一次,没有多余的操作,所以整体的时间复杂度为 O(N),每次操作的平均复杂度为 O(1)。
👉单调队列的实现👈
// MyQueue.h
#pragma once
#include <deque>
#include <iostream>
#include <vector>
#include <assert.h>
using namespace std;class MyQueue
{
public:// 因为范围是左必右开的,所以_left初始为-1,_right初始为0// [_left, _right)MyQueue(const vector<int>& arr): _arr(arr), _left(-1), _right(0){}void push(){// 数组中的元素都进入过单调队列中了if (_right == _arr.size())return;// 加入新元素时,将队尾元素弹出至队列为空或队尾元素大于新加入的元素while (!_q.empty() && _arr[_q.back()] <= _arr[_right]){_q.pop_back();}_q.push_back(_right);++_right;}// _arr [_left, _right)void pop(){// 左边界大于等于右边界,说明窗口内没有数据了,// 直接返回即可if (_left >= _right - 1)return;// 因为_left初始值是-1,所以需要先加加_left++_left;if (_q.front() == _left){_q.pop_front();}}int front(){// 如果队列为空,直接断言报错assert(!_q.empty()); return _arr[_q.front()];}private:int _left; // 窗口的左边界int _right; // 窗口的右边界的再右一个位置deque<int> _q; // 使用双端队列来实现单调队列,双端队列中存的是下标vector<int> _arr;
};
MyQueue 类使用说明:
- 申请一个滑动窗口对象时,需要传入一个 vector 对象。
- 上面的滑动窗口类可以自己手动控制滑动窗口的大小。使用一次 push 接口,就表明滑动窗口的右边界向右移动;而使用一次 pop 接口,就表明滑动窗口的左边界向右移动。滑动窗口左右边界向右移动,双端队列中存储的数据会是否需要弹出,见上文讲解!
知道如何使用 MyQueue 类后,我们就可以轻松地解决最开始的题目了。
注:需要将 MyQueue 类拷贝到 LeetCode 上
class Solution
{
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue q(nums);// 形成大小为k的窗口for(int i = 0; i < k; ++i){q.push();}vector<int> ret;ret.push_back(q.front()); // 将当前窗口中的最大值尾插到ret中for(int i = k; i < nums.size(); ++i){// 左右边界同时向右移动一次即可保存滑动窗口的大小为kq.push();q.pop();ret.push_back(q.front()); // 记录滑动窗口的最大值}return ret;}
};

注:单调队列的实现方式有很多,需要根据具体的题目来定制相应的单调队列,不能死板地认为单调队列只有一种实现方式。
👉单调栈的实现👈
单调栈也是具有单调性的栈,其存储的元素是单增或者单剪。单调栈通常用于寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置。
给定数组 arr = { 5 4 3 6 1 2 0 7 },请你求出数组中每个元素的左边和右边第一个比自己大的元素。暴力的方法,来到 i 位置,向左向右遍历找出第一个比 i 位置上元素大的元素。很明显,这种方式的时间复杂度为 O(N^2)。
如果采用单调栈呢,解决上面问题的时间复杂度为 O(N)。过程如下图:

为什么上面的过程就能够求出每个元素左边和右边第一个比自己大的元素呢?证明如下图:

如果数组中有重复的元素,那么栈中里面放的就不再是下标了,而是存储下标的 list 或者 vector。当新加入的元素比栈顶元素大时,那么就生成信息了。那如何生成呢?新加入的元素就是第一个比栈顶元素大的元素,栈顶元素下面压着的链表尾部的元素就是左边第一个比栈顶元素大的元素。如果新加入的元素和栈顶元素相等,那么新加入元素的下标尾插到 list 或 vector 中。
单调栈的实现,在这里我就不实现成一个类了,而将其实现出一个函数。如果大家想将其实现成一个类,可以参考下面的代码来实现。
数组无重复值版本的单调栈
vector<vector<int>> getNearBiggerNoRepeat1(const vector<int> arr)
{// ret[i][0]存的值是左边第一个比arr[i]大的值的下标// ret[i][1]存的值是右边第一个比arr[i]大的值的下标vector<vector<int>> ret(arr.size(), vector<int>(2));stack<int> st;for (int i = 0; i < arr.size(); ++i){// arr[i]为新插入的元素while (!st.empty() && arr[st.top()] < arr[i]){int popIndex = st.top();st.pop();// 如果左边没有比自己大的数,左边界的下标设置为-1int leftBiggerIndex = st.empty() ? -1 : st.top();ret[popIndex][0] = leftBiggerIndex;// 如果新插入元素比栈顶元素大,那么新插入元素就是// 右边第一个比栈顶元素大的元素ret[popIndex][1] = i;}// 添加元素操作不要忘了st.push(i);}// 生成栈中元素的信息while (!st.empty()){int popIndex = st.top();st.pop();// 如果左边没有比自己大的数,左边界的下标设置为-1int leftBiggerIndex = st.empty() ? -1 : st.top();ret[popIndex][0] = leftBiggerIndex;// 如果新插入元素比栈顶元素大,那么新插入元素就是// 右边第一个比栈顶元素大的元素ret[popIndex][1] = -1;}return ret;
}
现在数组无重复值版本的单调栈就实现好了,我们找到题目来验证一下写得对不对吧!
每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
很明显,每日温度这道题目就可以通过单调栈来解决。而且这道题目只要求求出右边第一个比自己大的值就行了,并不需要求左边第一个比自己大的值。那么就把上面的实现的单调栈代码拷贝到 LeetCode 去,再实现下面的代码就行了。
vector<vector<int>> getNearBiggerNoRepeat(const vector<int>& arr)
{// ret[i][0]存的值是左边第一个比arr[i]大的值的下标// ret[i][1]存的值是右边第一个比arr[i]大的值的下标vector<vector<int>> ret(arr.size(), vector<int>(2));stack<int> st;for (int i = 0; i < arr.size(); ++i){// arr[i]为新插入的元素while (!st.empty() && arr[st.top()] < arr[i]){int popIndex = st.top();st.pop();// 如果左边没有比自己大的数,左边界的下标设置为-1int leftBiggerIndex = st.empty() ? -1 : st.top();ret[popIndex][0] = leftBiggerIndex;ret[popIndex][1] = i;}// 添加元素操作不要忘了st.push(i);}// 生成栈中元素的信息while (!st.empty()){int popIndex = st.top();st.pop();int leftBiggerIndex = st.empty() ? -1 : st.top();ret[popIndex][0] = leftBiggerIndex;ret[popIndex][1] = -1;}return ret;
}class Solution
{
public:vector<int> dailyTemperatures(vector<int>& temperatures) {vector<vector<int>> info = getNearBiggerNoRepeat(temperatures);vector<int> ret(temperatures.size());for(size_t i = 0; i < temperatures.size(); ++i){// info[i][1] 等于 -1 表示 temperature[i] 右边没有比它更高的温度了// info[i][0] 不等于 -1 表示 temperature[i] 右边有比它更高的温度// 最近的一天是在 info[i][1] - i 天后if(info[i][1] != -1)ret[i] = info[i][1] - i;elseret[i] = 0;}return ret;}
};

用我们上面实现的单调栈来解决这道题目,简直就是杀鸡用牛刀。解决这道题目,我们只需要实现单调栈的主要逻辑就行了,如下方代码所示:
class Solution
{
public:vector<int> dailyTemperatures(vector<int>& temperatures) {vector<int> ret(temperatures.size());stack<int> st;st.push(0); // 数组第一个元素先入栈for(int i = 1; i < temperatures.size(); ++i){// 栈顶元素比新加入元素temperatures[i]小// 就要生成栈顶元素的信息while(!st.empty() && temperatures[st.top()] < temperatures[i]){int popIndex = st.top();st.pop();ret[popIndex] = i - popIndex;}st.push(i);}// 循环结束,栈中的元素也要生成信息while(!st.empty()){int popIndex = st.top();st.pop();ret[popIndex] = 0;}return ret;}
};

数组有重复值版本的单调栈
vector<vector<int>> getNearBiggerRepeat(const vector<int>& arr)
{// ret[i][0]存的值是左边第一个比arr[i]大的值的下标// ret[i][1]存的值是右边第一个比arr[i]大的值的下标vector<vector<int>> ret(arr.size(), vector<int>(2));stack<vector<int>> st;for (int i = 0; i < arr.size(); ++i){while (!st.empty() && arr[st.top()[0]] < arr[i]){vector<int> popVector = st.top();st.pop();int leftBiggerIndex = st.empty() ? -1 : st.top()[st.top().size() - 1];for (int popIndex : popVector){ret[popIndex][0] = leftBiggerIndex;ret[popIndex][1] = i;}}// 添加操作if (!st.empty() && arr[st.top()[0]] == arr[i]){st.top().push_back(i);}else{vector<int> v;v.push_back(i);st.push(v);}}while (!st.empty()){vector<int> popVector = st.top();st.pop();int leftBiggerIndex = st.empty() ? -1 : st.top()[st.top().size() - 1];for (int popIndex : popVector){ret[popIndex][0] = leftBiggerIndex;ret[popIndex][1] = -1;}}return ret;
}void Test()
{vector<int> arr = { 2, 3, 2, 5,6,7,3,3,3,5,8 };vector<vector<int>> ret = getNearBiggerRepeat(arr);for (int i = 0; i < ret.size(); ++i){cout << ret[i][0] << " : " << ret[i][1] << endl;}
}

指标A的最大值
数组中所有数都是正数,数组中累加和与最小值的乘积, 假设叫做指标 A。给定一个数组, 请返回子数组中, 指标 A 最大的值。
思路:求出数组中每个元素作为最小值时的指标 A,要使子数组的指标 A 最大,那么就要使子数组的累加和最大。那怎么才能让子数组的累加和最大呢?就是找到左边和右边第一个比自己小的元素,这样就能让子数组的累加和最大了。很明显,这就需要用到单调栈了。
class Solution
{
public:int max(vector<int>& arr){int max = -1;stack<int> st;st.push(0);for (int i = 1; i < arr.size(); ++i){// 该单调栈栈底元素是最大的,栈底元素是最小的while (!st.empty() && arr[st.top()] >= arr[i]){int popIndex = st.top();st.pop();// 栈为空时,说明从0到i-1的数中arr[popIndex]是最小的// 栈不为空时,说明从st.top()+1到i-1的数中arr[popIndex]是最小的int leftSmallerIndex = !st.empty() ? st.top() + 1 : 0;int sum = 0;for (int j = leftSmallerIndex; j < i; ++j){sum += arr[j];}max = sum * arr[popIndex] > max ? sum * arr[popIndex] : max;}st.push(i);}// 循环结束,栈中的元素右边全是比自己大的数while (!st.empty()){int popIndex = st.top();st.pop();// 栈为空时,说明从0到i-1的数中arr[popIndex]是最小的// 栈不为空时,说明从st.top()+1到i-1的数中arr[popIndex]是最小的int leftSmallerIndex = !st.empty() ? st.top() + 1 : 0;int sum = 0;for (int j = leftSmallerIndex; j < arr.size(); ++j){sum += arr[j];}max = sum * arr[popIndex] > max ? sum * arr[popIndex] : max;}return max;}
};

上面的代码还有可以优化的地方,就是先把前缀和存到一个数组中,需要累加和的时候直接取即可。
class Solution
{
public:int max(vector<int>& arr){int size = arr.size();vector<int> sum(size);sum[0] = arr[0];// 求前缀和for(int i = 1; i < size; ++i){sum[i] = sum[i - 1] + arr[i];}int ret = -1;stack<int> st;st.push(0);for(int i = 1; i < size; ++i){while(!st.empty() && arr[st.top()] >= arr[i]){int popIndex = st.top();st.pop();// 栈为空,说明popIndex左边没有比它小的数,累加和为sum[i-1]// 栈不为空,说明popIndex左边有比它小的数,累加和为sum[i-1] - sum[st.top()]int Sum = st.empty() ? sum[i - 1] : (sum[i - 1] - sum[st.top()]);ret = ret > (Sum * arr[popIndex]) ? ret : (Sum * arr[popIndex]);}st.push(i);}while(!st.empty()){int popIndex = st.top();st.pop();// 在栈中的元素,右边没有比它们小的元素了// 栈为空,说明popIndex左边没有比它小的数,累加和为sum[size-1]// 栈不为空,说明popIndex左边有比它小的数,累加和为sum[size-1] - sum[st.top()]int Sum = st.empty() ? sum[size - 1] : (sum[size - 1] - sum[st.top()]);ret = ret > (Sum * arr[popIndex]) ? ret : (Sum * arr[popIndex]);}return ret;}
};

👉总结👈
本篇博客主要讲解了两个非常实用的数据结构:单调队列和单调栈、用单调队列解决 LeetCode 中的滑动窗口最大值问题、用单调栈解决 LeetCode 中的每日问题和牛客网中的指标 A 的最大值问题等。那么以上就是本篇博客的全部内容了,如果大家觉得有收获的话,可以点个三连支持一下!谢谢大家!💖💝❣️
相关文章:

【数据结构与算法】单调队列 | 单调栈
🌠作者:阿亮joy. 🎆专栏:《数据结构与算法要啸着学》 🎇座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉…...

openh264解码h264视频帧主流程
一 解析一帧的入口int32_t WelsDecodeSlice (PWelsDecoderContext pCtx, bool bFirstSliceInLayer, PNalUnit pNalCur) {// 解码slicePDqLayer pCurDqLayer pCtx->pCurDqLayer;PFmo pFmo pCtx->pFmo;int32_t iRet;int32_t iNextMbXyIndex, iSliceIdc;PSlice pSlice &a…...

【个人笔记】C语言位域
一句话解释位域:指定结构体内变量的的位宽,从而节省空间 例子: #include <stdio.h> struct _test {int bit1:3; // 第一个字节0 ~ 2位 int :0; // 空域:表示第一个字节 3~7都为0int bit2:1; // 第二个字节第0位int :3;…...
——ROS的核心概念)
ROS笔记(1)——ROS的核心概念
目录 节点与管理器 话题通信 服务通信 参数——全局共享字典 节点与管理器 节点——执行单元 (1)执行具体任务的进程、独立运行的可执行文件 (2)不同节点可使用不同的编程语言,可分布式运行在不同的主机 ÿ…...
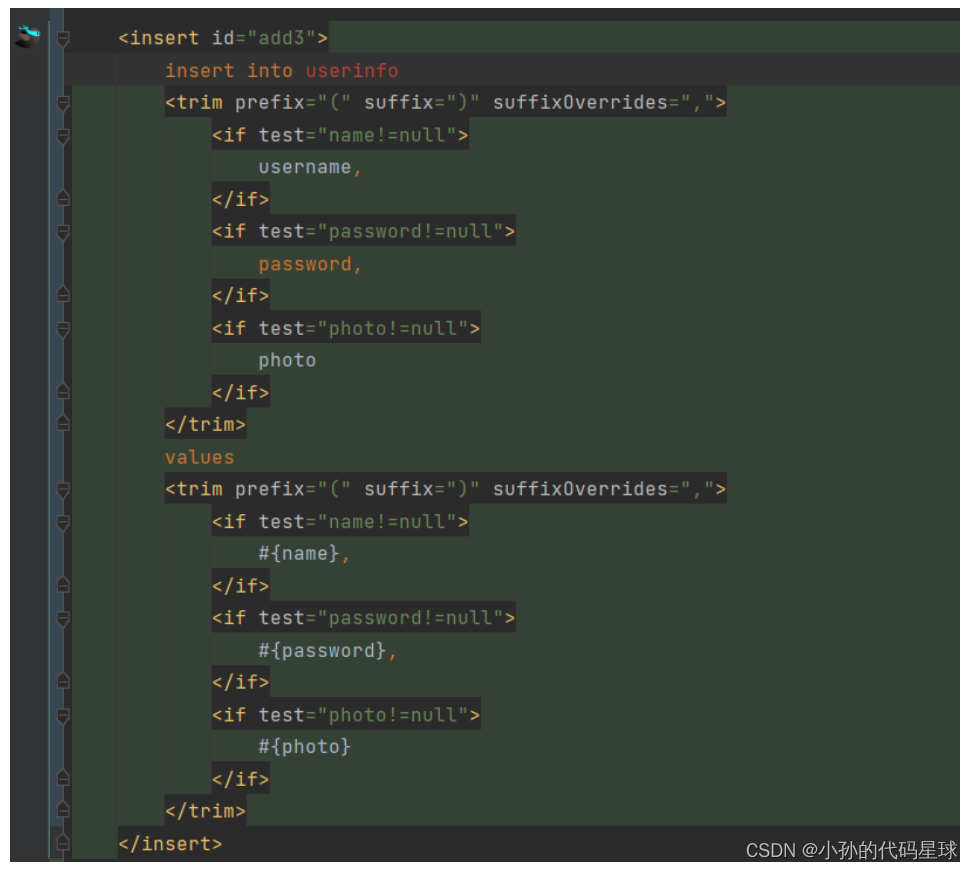
动态SQL使用【JavaEE】
动态SQL使用 1. if 标签 判断一个参数是否有值,如果没值,那么就会隐藏 if 中的 sql 语法: <if test"username!null">username#{username} </if>表达式:username 的参数是否为空 如果结果为 true,…...

leetcode刷题
1、stack栈相关 top():返回一个栈顶元素的引用,类型为 T&。如果栈为空,返回值未定义。 push(const T& obj):可以将对象副本压入栈顶。这是通过调用底层容器的 push_back() 函数完成的。 push(T&& obj)࿱…...

移动设备安全管理基础指南
什么是移动安全管理 (MSM) 移动安全管理是指为保护企业中的移动设备和企业数据而采取的行动。这些操作可以进一步被归类为反应性的或主动的,基于该操作是在数据和设备被破坏之前还是之后执行的。除了管理移动设备外,大多数MDM解决…...

【Java|多线程与高并发】 使用Thread 类创建线程的5种方法如何查看程序中的线程
文章目录前言线程创建1.继承Thread类重写run()方法如何查看程序中的线程?2.实现Runnable接口3.使用匿名内部类,继承Thread4.使用匿名内部类,实现Runnable5.⭐使用Lambda表达式,创建线程(重要)Thread 的常见构造方法总结前言 在这里主要补充说明一些问题,方便更好地理解下面的…...
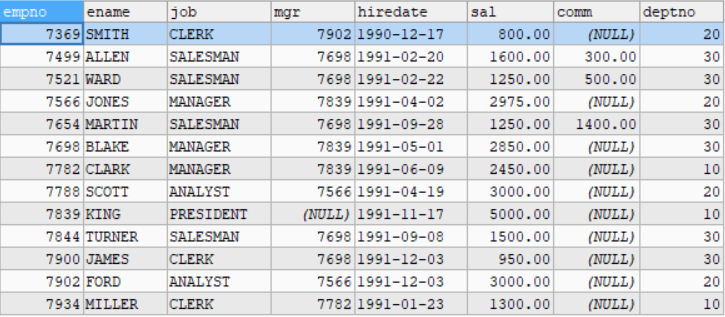
零基础学MySQL(五)-- 详细讲解数据库中的常用函数
目录🎇一、聚合函数1️⃣count 函数(1)基本语法(2)基本练习(3)注意细节2️⃣sum 函数(1)基本语法(2)基本练习(3)注意细节3…...

第4章 流程控制-if-else,Switch,For循环(循环守卫,循环步长,倒叙打印),While循环,多重循环...
第 4 章 流程控制-if-else,Switch,For循环(循环守卫,循环步长,倒叙打印),While循环,多重循环 4.1 分支控制 if-else 让程序有选择的的执行,分支控制有三种:单分支、双分支、多分支 4.1.1 单分支 1)基本语法…...
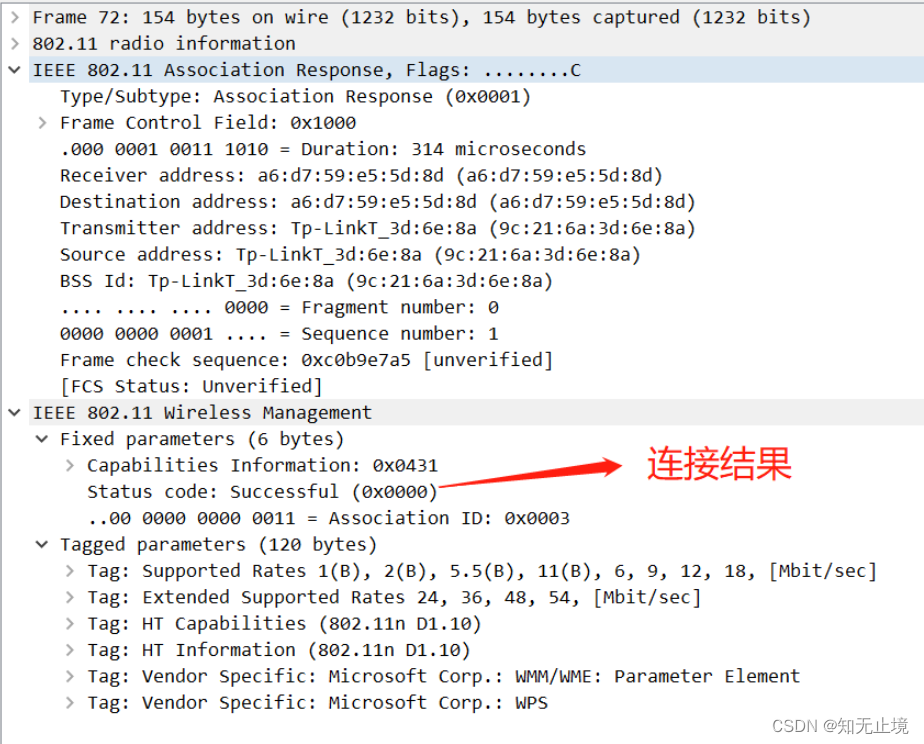
2.4G-WiFi连接路由器过程
一、概述 WiFi的数据通信基于802.11协议进行,无线AP在工作时会定时向空中发送beacon数据包,基站(STA)从beacon中解析出AP的名称、加密方式等信息,从而发起连接。 二、WiFi连接路由器的详细过程 WiFi连接过程主要可以…...
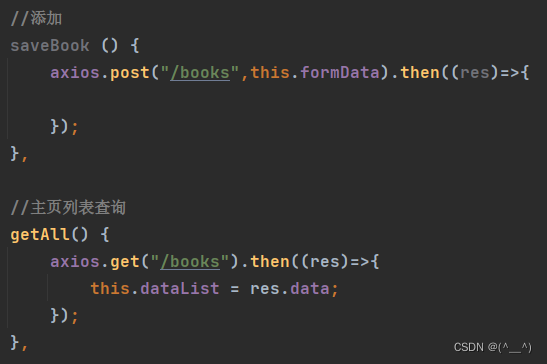
3. SpringMVC Rest 风格
1. REST 简介 REST(Representational State Transfer),表现形式状态转换,它是一种软件架构风格。 当要表示一个网络资源的时候,可以使用两种方式: 传统风格资源描述形式 http://localhost/user/getById?…...

Python3简介
Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python 的设计具有很强的可读性,相比其他语言经常使用英文关键字,其他语言的一些标点符号,它具有比其他语言更有特色语法结构。 Python 是面向对象语言: 这意味着P…...

如何学习PMP?
★基础要打牢 方法:“基础不牢,地动山摇”,如果基础不牢那么就很难拿高分,因为连最基础的题目分都不一定能拿到。 可以在针对基础知识,把PMBOK看一两遍,再次加深印象,再把平时做章节练习、每日5…...
【DSP视频教程】第11期:插补算法,曲线拟合丝滑顺畅,统计函数和基础函数加速实现,汇集SIMD,饱和和MAC乘累加应用实战(2023-02-12)
视频教程汇总帖:https://www.armbbs.cn/forum.php?modviewthread&tid110519 DSP视频教程有段时间没有更新了。 当前DSP库从CMSIS软件包里面独立出来,并且更新非常频繁,所以本期视频教程优先给大家简单介绍下新版DSP, 然后为…...

分类模型评估:混淆矩阵、准确率、召回率、ROC
1. 混淆矩阵 在二分类问题中,混淆矩阵被用来度量模型的准确率。因为在二分类问题中单一样本的预测结果只有Yes or No,即:真或者假两种结果,所以全体样本的经二分类模型处理后,处理结果不外乎四种情况,每种…...
算法 ——世界 一
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。个人爱好: 编程,打篮球,计算机知识个人名言:海不辞水,故能成其大;山不辞石…...

2023年3月AMA-CDGA/CDGP数据治理认证考试这些城市可以报名
目前2023年3月5日CDGA&CDGP开放报名的城市有:北京、上海、广州、深圳、杭州、重庆,西安,成都,长沙,济南,更多考场正在增加中… DAMA认证为数据管理专业人士提供职业目标晋升规划,彰显了职业…...

Java变量和数据类型,超详细整理,适合新手入门
目录 一、什么是变量? 二、变量 变量值互换 三、基本数据类型 1、八种基本数据类型 2、布尔值 3、字符串 四、从控制台输入 一、什么是变量? 变量是一种存储值的容器,它可以在程序的不同部分之间共享;变量可以存储数字、字…...

Echarts 设置折线图拐点的颜色,边框等样式,hover时改变颜色
第014个点击查看专栏目录上一篇文章我们讲到了如何设置拐点大小,图形类型,旋转角度,缩放同比,位置偏移等,这篇文章介绍如何设置拐点的颜色、边框大小颜色等样式。hover轴线时候,拐点的填充颜色改变文章目录示例效果示例…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...




