【Fermat】费马小定理

定理
若存在整数 a , p 且g c d ( a , p ) = 1 gcd(a,p)=1gcd(a,p)=1,即二者互为质数,则有
a ( p − 1 ) ≡ 1 ( m o d p ) a^{(p-1)}≡ 1(mod p)
a
(p−1)
≡1(modp)
目录
定理
引理
引理一
引理二
证明
应用
代码
引理
引理一
若a,b,c为任意3个整数,m为正整数,且g c d ( m , c ) = 1 gcd(m,c)=1gcd(m,c)=1,则当a ∗ c ≡ b ∗ c ( m o d m ) a*c\equiv b*c(mod\ m)a∗c≡b∗c(mod m)时,有a ≡ b ( m o d m ) a\equiv b(mod\ m)a≡b(mod m)。
引理二
设m是一个整数且m>1,b是一个整数且(m,b)=1。如果a[1],a[2],a[3],a[4],…a[m]是模m的一个完全剩余系,则b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也构成模m的一个完全剩余系。
证明
若存在2个整数b·a[i]和b·a[j]同余即b·a[i]≡b·a[j](mod m)…(i>=1 && j>=1),根据引理1则有a[i]≡a[j](mod m)。根据完全剩余系的定义可知这是不可能的,因此不存在2个整数b·a[i]和b·a[j]同余。
所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]构成模m的一个完全剩余系。
构造素数 的完全剩余系
p={1,2,3,…,p-1}.
因为 ,由引理2可得
A={a,2a,3a,…,(p-1)a}.
也是p的一个完全剩余系。由完全剩余系的性质,
123*…(p-1)≡a2a3a…*(p-1)a(mod p).
即
( p − 1 ) ! ≡ ( p − 1 ) ! ∗ a ( p − 1 ) ( m o d p ) (p-1)!≡(p-1)!*a^{(p-1)}(mod\ p)(p−1)!≡(p−1)!∗a
(p−1)
(mod p)
易知 ((p-1)!,p)=1,同余式两边可约去(p-1)!,得到
a ( p − 1 ) ≡ 1 ( m o d p ) a^{(p-1)}≡1(mod p)a
(p−1)
≡1(modp)
逆元:ax≡1(mod p)当a和p互质时,方程的解 x 称为a关于p的逆元,
在普通的四则运算中,只有加减乘三种运算可以进行分别取余运算,因为这三种运算都是从低位到高位的运算,而对于除法是从高位到低位的运算,显然不能直接进行取余,这时候,就要用到逆元有关的运算。
逆元可以近似的看作倒数的概念
应用
例如,
如果要求(x / y)%p ,显然不可以(x%p)/(y%p),
利用逆元运算:可以将(x / y)%p化为 (x * Y )%p ,其中Y是y关于p的逆元
那么怎么求Y呢:
由逆元的定义,有y • Y≡1(mod p),
费马小定理:如果p是一个质数,而整数a不是p的倍数,则有a^(p-1)≡ 1(mod p)。
我们分离一项出来 a • a ( p − 2 ) ≡ 1 ( m o d p ) a • a^{(p-2)} ≡ 1(mod\ p)a•a
(p−2)
≡1(mod p).
对比逆元的方程式,可以很容易得到,a关于p的逆元就是 a ( p − 2 ) a^{(p-2)}a
(p−2)
,那么Y = y ( p − 2 ) 。 Y=y^{(p-2)}。Y=y
(p−2)
。
代码
根据上述推断,根据快速幂可推得:
/* 除法取模模板 */
ll quick(ll a,ll b,ll c)//快速幂取模
{ll ans=1;a%=c;while(b){if(b&1) ans=ans*a%c;a=a*a%c;b>>=1;} return ans%c;
}ll divi(ll a,ll b,ll p)
{b=quick(b,p-2,p); //b的逆元return a*b%p;
}
相关文章:

【Fermat】费马小定理
定理 若存在整数 a , p 且g c d ( a , p ) 1 gcd(a,p)1gcd(a,p)1,即二者互为质数,则有 a ( p − 1 ) ≡ 1 ( m o d p ) a^{(p-1)}≡ 1(mod p) a (p−1) ≡1(modp) 目录 定理 引理 引理一 引理二 证…...
非易失性存储器访问和传输协议)
NVMe(Non-Volatile Memory Express)非易失性存储器访问和传输协议
目录 NVMe(Non-Volatile Memory Express)非易失性存储器访问和传输协议 一、NVMe的定义 二、NVMe的特点 三、NVMe的应用场景 四、举例说明 NVMe(Non-Volatile Memory Express)非易失性存储器访问和传输协议 是一种非易失性存储器访问和传输协议,专为固态硬盘(SSD)…...

C++初阶——queue
一、什么是queue 是一个容器适配器,专门设计用于在先进先出(FIFO,First In First Out)的上下文中操作。它是一个容器适配器,这意味着它不是一个完整的容器类,而是封装了一个特定的容器类(如list…...

达梦数据库迁移j脚本
国产环境使用达梦数据库的越来越多,除了使用管理工具,还是可以使用脚本。 下面简单记录下,我在迁移中遇到的问题: 备份脚本 使用此脚本可以一次备份一个数据 backup_one_db.sh #!/bin/bashexport DB$1 export PASS<your_p…...

【Linux】内核调用栈打印函数dump_stack使用效果
init/main.c的start_kernel示例,这个调用栈不太深: /var/log/dmesg日志: [ 0.000000] kernel: [init/main.c start_kernel 911] start_kernel(void) [ 0.000000] kernel: [kernel/panic.c print_tainted 519 LOG_TIMES: 1 ] [ 0.…...

Uniapp踩坑input自动获取焦点ref动态获取实例不可用
前言 大家好我是没钱的君子下流坯,用自己的话解释自己的知识。很久很更新了,这几个月一直在加班,今天记录一个uniapp关于input中focus()方法自动获取焦点的坑。 案例 为了实现一个手机验证码的页面,验证码是五个输入框…...

数据分析-47-时间序列变点检测之离线历史数据的CPD
文章目录 1 时间序列结构1.1 变化点的定义1.2 结构变化的类型1.2.1 水平变化1.2.2 方差变化1.3 变点检测1.3.1 离线数据检测方法1.3.2 实时数据检测方法2 模拟数据2.1 模拟恒定方差数据2.2 模拟变化方差数据3 离线数据变点检测3.1 Ruptures模块3.2 恒定方差CPD3.3 变化方差CPD4…...

加入GitHub Spark需要申请
目录 加入GitHub Spark需要申请 GitHub Spark 一、产品定位与特点 二、核心组件与功能 三、支持的AI模型 四、应用场景与示例 五、未来展望 六、申请体验 加入GitHub Spark需要申请 GitHub Spark 是微软旗下GitHub在2024年10月30日的GitHub Universe大会上推出的一款革…...

生成式GPT商品推荐:精准满足用户需求
生成式GPT商品推荐:精准满足用户需求 随着人工智能(AI)技术的飞速发展,电商平台正在逐步迎来一场前所未有的变革。尤其是生成式GPT(Generative Pre-trained Transformer)技术的应用,正在重新定…...

async 和 await的使用
一、需求 点击按钮处理重复提交,想要通过disabled的方式实现。 但是点击按钮调用的方法里有ajax、跳转、弹窗等一系列逻辑操作,需要等方法里流程都走完,再把disabled设为false,这样下次点击按钮时就可以继续走方法里的ajax等操作…...
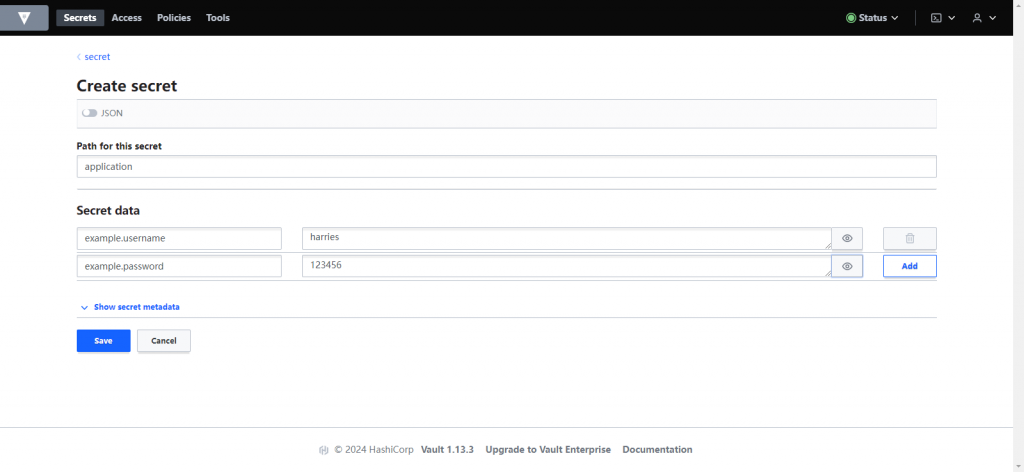
Spring Cloud Vault快速入门Demo
1.什么是Spring Cloud Vault? Spring Cloud Vault 是 Spring Cloud 生态系统中的一个项目,旨在简化 Spring 应用程序与 HashiCorp Vault 的集成。它提供了一种方便的方式来管理和访问应用程序的敏感配置数据,如数据库凭证、API 密钥和其他机…...

道陟科技EMB产品开发进展与标准设计的建议|2024电动汽车智能底盘大会
11月12日,2024电动汽车智能底盘大会在重庆开幕。会议由中国汽车工程学会主办,电动汽车产业技术创新战略联盟、中国汽车工程学会智能底盘分会、智能绿色车辆与交通全国重点实验室承办。本届大会围绕电动汽车智能底盘相关技术发展与融合,满足高…...

GitHub Org
运营一个GitHub Org(组织)是一个复杂但充满价值的过程,它涉及多个方面,包括项目管理、团队协作、代码审查、文档维护、社区建设等。以下是一篇关于如何运营GitHub Org的详细指南,旨在帮助组织者更好地管理和维护其GitH…...

unity小:shaderGraph不规则涟漪、波纹效果
实现概述 在本项目中,我们通过结合 Sine、Polar Coordinates 和 Time 节点,实现了动态波纹效果。以下是实现细节: 核心实现 Sine 波形生成: 使用 Sine 节点生成基本的波形。该节点能够创建周期性变化,为波纹效果提供…...

【JavaScript】JavaScript开篇基础(6)
1.❤️❤️前言~🥳🎉🎉🎉 Hello, Hello~ 亲爱的朋友们👋👋,这里是E绵绵呀✍️✍️。 如果你喜欢这篇文章,请别吝啬你的点赞❤️❤️和收藏📖📖。如果你对我的…...

Spark RDD、DStream、DataFrame、DataSet 在窗口操作上的区别
Spark RDD、DStream、DataFrame、DataSet 在窗口操作上的区别 1. Spark RDD 是否支持窗口操作: RDD 本身没有专门的窗口操作算子。原因: RDD 是一个弹性分布式数据集,设计为通用的、不可变的操作单元,主要用于批处理场景。窗口函…...

http自动发送请求工具(自动化测试http请求)
点击下载《http自动发送请求工具(自动化测试http请求)》 前言 在现代软件开发过程中,HTTP 请求的自动化测试是确保应用程序稳定性和可靠性的关键环节。为了满足这一需求,我开发了一款功能强大且易于使用的自动化 HTTP 请求发送工具。该工具基于 C# 开发…...

网络IP地址会经常换吗?深入解析与实操指南
在互联网的生态系统中,IP地址(Internet Protocol Address)是每台连接设备的唯一标识符,它在网络通信中起着至关重要的作用。然而,不少用户观察到自己的IP地址有时会发生变化,这引发了诸多疑问。本文旨在详细…...

MapLocNet由粗到细的定位网络
论文链接 MapLocNet: Coarse-to-Fine Feature Registration for Visual Re-Localization in Navigation Mapshttps://arxiv.org/html/2407.08561v1 问题背景 当前自动驾驶的定位主要依赖于高精度的地图和GPS信号,但在城市环境中,GPS信号易受到多路径传…...

【Docker】Mac安装Docker Desktop导致磁盘剩余空间较少问题如何解决?
目录 一、背景描述 二、解决办法 三、清理效果 四、理论参考 解决方法 1. 清理未使用的 Docker 镜像、容器和卷 2. 查看 Docker 使用的磁盘空间 3. 调整 Docker 的存储位置 4. 增加磁盘空间 5. 调整 Docker Desktop 配置 6. 使用 Docker 清理工具(例如 D…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
