手搓神经网络(MLP)解决MNIST手写数字识别问题 | 数学推导+代码实现 | 仅用numpy,tensor和torch基本计算 | 含正反向传播数学推导
手写数字识别(神经网络入门)
文章目录
- 手写数字识别(神经网络入门)
- 实验概述
- 实验过程
- 数据准备
- 模型实现
- 线性变换层
- 前向传播
- 反向传播
- 更新参数
- 整体实现
- 激活函数层(ReLU)
- 前向传播
- 反向传播
- 整体实现
- Softmax层(含交叉熵损失函数)
- 前向传播
- 交叉熵损失
- 反向传播
- 整体实现
- 含单隐藏层的前馈神经网络(MLP)
- 训练评估
实验概述
仅使用numpy和pytorch中的tensor库(以及torch中相关基本计算方法)手动实现含单隐藏层的前馈神经网络模型以及反向梯度传播的学习过程,来进行MNIST数据集上的手写数字识别。
实验过程
数据准备
首先,在 MNIST官网 下载手写数字数据集,保存至本地 data_folder 并解压:
import gzip
import shutil
import osdata_folder = "../data"for file_name in os.listdir(data_folder):if file_name.endswith(".gz"):file_path = os.path.join(data_folder, file_name)out_path = file_path.replace(".gz", "") # 解压后的文件路径# 解压文件with gzip.open(file_path, 'rb') as in_file:with open(out_path, 'wb') as out_file:shutil.copyfileobj(in_file, out_file)
根据官网提供的数据格式说明,载入图片和标签数据:
import numpy as npdef load_images(file_path):""" 载入图片数据 """with open(file_path, 'rb') as f:f.read(16) # 根据MNIST数据集格式,跳过元数据data = np.frombuffer(f.read(), dtype=np.uint8)data = data.reshape(-1, 28, 28) # 每张图片为 28x28 的灰度值图片return datadef load_labels(file_path):""" 载入标签数据 """with open(file_path, 'rb') as f:f.read(8) # 根据MNIST数据集格式,跳过元数据labels = np.frombuffer(f.read(), dtype=np.uint8)return labelstrain_images = load_images(data_folder + "/train-images-idx3-ubyte")
train_labels = load_labels(data_folder + "/train-labels-idx1-ubyte")
test_images = load_images(data_folder + "/t10k-images-idx3-ubyte")
test_labels = load_labels(data_folder + "/t10k-labels-idx1-ubyte")
可视化一部分数据作检查:
import matplotlib.pyplot as pltdef visualize(images, labels, num_samples=10):plt.figure(figsize=(10, 2))for i in range(num_samples):plt.subplot(1, num_samples, i + 1)plt.imshow(images[i], cmap='gray')plt.title(f"Label: {labels[i]}")plt.axis('off')plt.show()visualize(train_images, train_labels) # 可视化训练集的前10张图像
visualize(test_images, test_labels) # 可视化测试集的前10张图像
可以看到,数据已经正确载入:

下面,进行一些数据预处理。
为了加速后续计算,将数据放到tensor中:
import torchmy_device = torch.device("cuda" if torch.cuda.is_available() else "cpu")train_images_tensor = torch.tensor(train_images, dtype=torch.float32, device=my_device)
train_labels_tensor = torch.tensor(train_labels, dtype=torch.long, device=my_device)
test_images_tensor = torch.tensor(test_images, dtype=torch.float32, device=my_device)
test_labels_tensor = torch.tensor(test_labels, dtype=torch.long, device=my_device)
将数据展平并归一化,便于后续神经网络的数据输入:
train_images_tensor = train_images_tensor.flatten(start_dim=1) / 255.0
test_images_tensor = test_images_tensor.flatten(start_dim=1) / 255.0
手动实现Dataset和DataLoader类,便于后续训练时按批次加载数据:
class MyDataset:def __init__(self, images, labels):self.images = imagesself.labels = labelsdef __len__(self):return len(self.images)def __getitem__(self, id):return self.images[id], self.labels[id]class MyDataLoader:def __init__(self, dataset, batch_size=1, shuffle=False, device='cpu'):self.dataset = datasetself.batch_size = batch_sizeself.shuffle = shuffleself.ids = np.arange(len(dataset)) # 索引列表self.cur_id = 0self.device = devicedef __iter__(self):self.cur_id = 0 # 重置索引if self.shuffle:np.random.shuffle(self.ids) # 打乱索引return selfdef __next__(self):if self.cur_id >= len(self.dataset):raise StopIteration# 获取一个batch的索引batch_ids = self.ids[self.cur_id : self.cur_id + self.batch_size]# 获取一个batch的对应数据batch_data = [self.dataset[i] for i in batch_ids]# 返回一个batch的图片和标签(并改为tensor类型)images, labels = zip(*batch_data)images = torch.stack(images).to(self.device)labels = torch.tensor(labels).to(self.device)self.cur_id += self.batch_sizereturn images, labelsdef __len__(self):""" 数据集的大小,即总批次数量 """return int(np.ceil(len(self.dataset) / self.batch_size))
用上述DataLoader包装数据:
train_set = MyDataset(train_images_tensor, train_labels_tensor)
test_set = MyDataset(test_images_tensor, test_labels_tensor)train_loader = MyDataLoader(train_set, batch_size=64, shuffle=True, device=my_device)
test_loader = MyDataLoader(test_set, batch_size=64, shuffle=False, device=my_device)
模型实现
📍
首先,需要实现线性层、激活函数(ReLU)、Softmax函数、损失函数(交叉熵损失)等组件。
同时,由于后续神经网络中的前向&反向传播也要手动实现,故上述组件的
forward和backward方法也需要先定义好。
线性变换层
前向传播
线性变换的数学定义为:
y = x W T + b y = xW^T + b y=xWT+b
其中:
- x x x 是大小为 i n p u t _ s i z e input\_size input_size 输入向量
- W W W 是形状为 ( o u t p u t _ s i z e , i n p u t _ s i z e ) (output\_size, input\_size) (output_size,input_size) 的权重矩阵
- b b b 是大小为 o u t p u t _ s i z e output\_size output_size 的偏置项
- y y y 是大小为 o u t p u t _ s i z e output\_size output_size 的输出向量
据此,可写出线性层的前向传播代码:
def forward(self, x):""" 前向传播 """self.x = x.to(self.device)y = torch.matmul(x, self.weights.T) + self.biasreturn y
反向传播
在反向传播过程中,需要计算各参数(即 W W W 和 b b b )的梯度以更新参数,并计算本层输入的梯度传回上一层。
首先,损失 L L L 对线性层输出 y y y 的梯度为 ∂ L ∂ y \frac{\partial L}{\partial y} ∂y∂L ,该梯度会由下一层反向传播回来。
后续代码中,下一层传回本层的梯度均记作
grad_out(out表示是对本层输出的梯度)
计算 L L L 对 W W W 的梯度 ∂ L ∂ W \frac{\partial L}{\partial W} ∂W∂L ,根据链式法则有:
∂ L ∂ W = ∂ L ∂ y ⋅ ∂ y ∂ W \frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial W} ∂W∂L=∂y∂L⋅∂W∂y
其中, ∂ y ∂ W \frac{\partial y}{\partial W} ∂W∂y 即在线性变换 y = x W T + b y = xW^T + b y=xWT+b 中对 W W W 求偏导,易得结果为 x x x ,所以 W W W 的反向传播公式为:
∂ L ∂ W = ∂ L ∂ y ⋅ x \frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} \cdot x ∂W∂L=∂y∂L⋅x
代码层面,考虑按批次训练,则 ∂ L ∂ y \frac{\partial L}{\partial y} ∂y∂L 是形状为 ( b a t c h _ s i z e , o u t p u t _ s i z e ) (batch\_size, output\_size) (batch_size,output_size) 的梯度矩阵, x x x 是形状为 ( b a t c h _ s i z e , i n p u t _ s i z e ) (batch\_size, input\_size) (batch_size,input_size) 的输入矩阵,故它们相乘时前者需要转置:
self.grad_weights = torch.matmul(grad_out.T, self.x)
计算 L L L 对 b b b 的梯度 ∂ L ∂ b \frac{\partial L}{\partial b} ∂b∂L ,根据链式法则有:
∂ L ∂ b = ∂ L ∂ y ⋅ ∂ y ∂ b \frac{\partial L}{\partial b} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial b} ∂b∂L=∂y∂L⋅∂b∂y
其中, ∂ y ∂ b \frac{\partial y}{\partial b} ∂b∂y 即在线性变换 y = x W T + b y = xW^T + b y=xWT+b 中对 b b b 求偏导,易得结果为 1 1 1 ,所以 b b b 的反向传播公式为:
∂ L ∂ b = ∂ L ∂ y \frac{\partial L}{\partial b} = \frac{\partial L}{\partial y} ∂b∂L=∂y∂L
代码层面,考虑按批次训练,即 ∂ L ∂ b = ∑ i = 1 b a t c h _ s i z e ∂ L ∂ y i \frac{\partial L}{\partial b} = \sum^{batch\_size}_{i =1}\frac{\partial L}{\partial y_i} ∂b∂L=∑i=1batch_size∂yi∂L ,有:
self.grad_bias = torch.sum(grad_out, dim=0)
计算 L L L 对线性层输入 x x x 的梯度 ∂ L ∂ x \frac{\partial L}{\partial x} ∂x∂L ,根据链式法则有:
∂ L ∂ x = ∂ L ∂ y ⋅ ∂ y ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x} ∂x∂L=∂y∂L⋅∂x∂y
其中, ∂ y ∂ x \frac{\partial y}{\partial x} ∂x∂y 即在线性变换 y = x W T + b y = xW^T + b y=xWT+b 中对 x x x 求偏导,易得结果为 W W W ,所以 x x x 的反向传播公式为:
∂ L ∂ x = ∂ L ∂ y ⋅ W \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot W ∂x∂L=∂y∂L⋅W
相应代码为:
grad_in = torch.matmul(grad_out, self.weights)
后续代码中,本层传给上一层的梯度均记作
grad_in(in表示是对本层输入的梯度)
更新参数
根据上面计算出的参数梯度,按照梯度下降法更新参数:
W ← W − η ⋅ ∂ L ∂ W b ← b − η ⋅ ∂ L ∂ b W \leftarrow W - \eta \cdot \frac{\partial L}{\partial W} \\ b \leftarrow b - \eta \cdot \frac{\partial L}{\partial b} W←W−η⋅∂W∂Lb←b−η⋅∂b∂L
其中 η \eta η 为学习率。
据此写出相应代码为:
def update(self, lr):""" 更新参数 """self.weights = self.weights - lr * self.grad_weightsself.bias = self.bias - lr * self.grad_bias
其中 lr 为学习率。
整体实现
综上,线性层组件的整体代码实现为:
class MyLinear():""" 线性变换层Args:input_size (int): 输入特征的数量output_size (int): 输出特征的数量Examples:>>> input = torch.randn(128, 20)>>> m = MyLinear(20, 30)>>> output = m.forward(input)>>> print(output.size())torch.Size([128, 30])"""def __init__(self, input_size, output_size, device="cpu"):# 正态随机初始化权重和偏置self.device = deviceself.weights = torch.randn(output_size, input_size, device=self.device)self.bias = torch.randn(output_size, device=self.device)def forward(self, x):""" 前向传播 """self.x = x.to(self.device)y = torch.matmul(x, self.weights.T) + self.biasreturn ydef backward(self, grad_out):""" 反向传播 """self.grad_weights = torch.matmul(grad_out.T, self.x)self.grad_bias = torch.sum(grad_out, dim=0)grad_in = torch.matmul(grad_out, self.weights)return grad_indef update(self, lr):""" 更新参数 """self.weights = self.weights - lr * self.grad_weightsself.bias = self.bias - lr * self.grad_bias
激活函数层(ReLU)
前向传播
ReLU函数的数学定义为:
y = R e L U ( x ) = { x , x > 0 0 , x ≤ 0 y = ReLU(x) = \begin{cases} x, \ x >0 \\ 0, \ x \le 0 \end{cases} y=ReLU(x)={x, x>00, x≤0
据此,可写出ReLU层的前向传播代码:
def forward(self, x):self.x = xy = torch.maximum(x, torch.tensor(0.0))return y
反向传播
计算ReLU层的梯度,即损失 L L L 对输入 x x x 的偏导数 ∂ L ∂ x \frac{\partial L}{\partial x} ∂x∂L 。由于反向传播过程中,下一层会传回 L L L 对ReLU输出 y y y 的梯度 ∂ L ∂ y \frac{\partial L}{\partial y} ∂y∂L ,故根据链式法则ReLU的梯度可以写成
∂ L ∂ x = ∂ L ∂ y ⋅ ∂ y ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x} ∂x∂L=∂y∂L⋅∂x∂y
其中, ∂ y ∂ x \frac{\partial y}{\partial x} ∂x∂y 即对 R e L U ( x ) ReLU(x) ReLU(x) 求导,易得:
∂ y ∂ x = { 1 , x > 0 0 , x ≤ 0 \frac{\partial y}{\partial x} = \begin{cases} 1, \ x >0 \\ 0, \ x \le 0 \end{cases} ∂x∂y={1, x>00, x≤0
所以,ReLU的反向传播公式为:
∂ L ∂ x = ∂ L ∂ y ⋅ { 1 , x > 0 0 , x ≤ 0 = { ∂ L ∂ y , x > 0 0 , x ≤ 0 \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \begin{cases} 1, \ x >0 \\ 0, \ x \le 0 \end{cases} = \begin{cases} \frac{\partial L}{\partial y}, \ x >0 \\ 0, \quad x \le 0 \\ \end{cases} ∂x∂L=∂y∂L⋅{1, x>00, x≤0={∂y∂L, x>00,x≤0
根据上面的公式,可以写出反向传播代码:
def backward(self, grad_output):grad_input = grad_output.clone()grad_input[self.x <= 0] = 0 # 对于非正的输入,梯度为零return grad_input
整体实现
综上,ReLU组件的整体代码实现为:
class ReLU:def forward(self, x):self.x = x # 保存输入以便后向传播使用return torch.maximum(x, torch.tensor(0.0))def backward(self, grad_output):grad_input = grad_output.clone()grad_input[self.x <= 0] = 0 # 对于小于零的输入,梯度为零return grad_input
Softmax层(含交叉熵损失函数)
前向传播
Softmax函数的数学定义为:
对于输入向量 x = [ x 1 , x 2 , … , x n ] \ x = [x_1, \ x_2, \dots, \ x_n] x=[x1, x2,…, xn] ,Softmax的输出向量 y ^ = [ y ^ 1 , y ^ 2 , … , y ^ n ] \hat{y} = [\hat{y}_1, \ \hat{y}_2, \dots, \ \hat{y}_n] y^=[y^1, y^2,…, y^n] 中的每个元素 y ^ i \hat{y}_i y^i 有
y ^ i = S o f t m a x ( x i ) = e x i ∑ j = 1 n e x j , j = 1 , 2 , … , n \hat{y}_i = Softmax(x_i) = \frac{e^{x_i}}{\sum^{n}_{j=1} e^{x_j}}, \ \ j = 1,2,\dots,n y^i=Softmax(xi)=∑j=1nexjexi, j=1,2,…,n
故Softmax的输出 y ^ \hat{y} y^ 是一个概率分布(代码中将其记作 probs ),据此可写出其前向传播代码:
def forward(self, x):x_max = torch.max(x, dim=1, keepdim=True) # 防止溢出,减去最大值来增加数值稳定性x_exp = torch.exp(x - x_max.values)self.probs = x_exp / torch.sum(x_exp, dim=1, keepdim=True)return self.probs
交叉熵损失
交叉熵(cross entropy)的数学定义为:
H ( p , q ) = − ∑ x p ( x ) log q ( x ) H(p, q) = - \sum_{x}p(x) \log{q(x)} H(p,q)=−x∑p(x)logq(x)
其中 p , q p, q p,q 是两个概率分布。因此本实验中,可以先将实际标签进行one-hot编码,则对于每个样本,其交叉熵损失函数为:
L ( y , y ^ ) = − ∑ j = 1 C y j log y j ^ L(y, \ \hat{y}) = -\sum^{C}_{j=1} y_j \log{\hat{y_j}} L(y, y^)=−j=1∑Cyjlogyj^
其中:
- C C C 是类别数(本实验中为10)
- y y y 是该样本的真实标签(one-hot分布), y j y_j yj 表示其在标签 j j j 上的one-hot值(0或1)
- y ^ \hat{y} y^ 是该样本的预测标签(概率分布), y j ^ \hat{y_j} yj^ 表示预测的该样本属于标签 j j j 的概率(由softmax得出)
因此,对于每一批次的 N N N 个样本,可得其mini-batch损失为:
L = − 1 N ∑ i = 1 N ∑ j = 1 C y j log y j ^ L = - \frac{1}{N} \sum^{N}_{i=1} \sum^{C}_{j=1}{y_j \log{\hat{y_j}}} L=−N1i=1∑Nj=1∑Cyjlogyj^
据此,可写出交叉熵损失函数代码:
def cross_entropy(self, predictions, truths):probs = self.probs # Softmax得到的预测标签的概率分布# 设定一个最小值min_val,防止log(0)min_val = 1e-6probs = torch.where(probs < min_val, torch.full_like(probs, min_val), probs)# 计算交叉熵损失batch_size = predictions.shape[0]truth_onehot = torch.zeros(batch_size, probs.shape[1], device=my_device)truth_onehot[torch.arange(batch_size), truths] = 1loss = -torch.mean(torch.sum(truth_onehot * torch.log(probs), dim=1))self.batch_size = batch_size # 批次大小self.truth_onehot = truth_onehot # 真实标签的one-hot分布return loss
反向传播
计算Softmax层的梯度,即 L L L 对输入 x x x 的偏导数 ∂ L ∂ x \frac{\partial{L}}{\partial{x}} ∂x∂L 。根据链式法则,可将其写成
∂ L ∂ x = ∂ L ∂ y ^ ⋅ ∂ y ^ ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial{\hat{y}}} \cdot \frac{\partial{\hat{y}}}{\partial x} ∂x∂L=∂y^∂L⋅∂x∂y^
故对于 x x x 中的某个样本 x i x_i xi ,有
∂ L ∂ x i = ∂ L ∂ y ^ ⋅ ∂ y ^ ∂ x i ( 1 ) \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial{\hat{y}}} \cdot \frac{\partial{\hat{y}}}{\partial x_i} \quad (1) ∂xi∂L=∂y^∂L⋅∂xi∂y^(1)
其中 y ^ \hat{y} y^ 是Softmax层的输出。根据上面的Softmax公式,对于某个样本有:
∂ L ∂ y ^ j = ∂ ( − ∑ j = 1 C y j log y ^ j ) ∂ y ^ j = − y j y ^ j ( 2 ) \frac{\partial L}{\partial{\hat{y}_j}} = \frac{\partial{(-\sum^{C}_{j=1} y_j \log{\hat{y}_j}})}{\partial{\hat{y}_j}} = - \frac{y_j}{\hat{y}_j} \quad (2) ∂y^j∂L=∂y^j∂(−∑j=1Cyjlogy^j)=−y^jyj(2)
将 ( 1 ) (1) (1) 展开后可带入 ( 2 ) (2) (2) :
∂ L ∂ x i = ∂ L ∂ y ^ ⋅ ∂ y ^ ∂ x i = ∑ j = 1 n ∂ L ∂ y ^ j ⋅ ∂ y ^ j ∂ x i = − ∑ j = 1 n y j y ^ j ⋅ ∂ y ^ j ∂ x i ( 3 ) \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial{\hat{y}}} \cdot \frac{\partial{\hat{y}}}{\partial x_i} = \sum^{n}_{j=1} \frac{\partial L}{\partial{\hat{y}_j}} \cdot \frac{\partial{\hat{y}_j}}{\partial x_i} = - \sum^{n}_{j=1} \frac{y_j}{\hat{y}_j} \cdot \frac{\partial{\hat{y}_j}}{\partial x_i} \quad (3) ∂xi∂L=∂y^∂L⋅∂xi∂y^=j=1∑n∂y^j∂L⋅∂xi∂y^j=−j=1∑ny^jyj⋅∂xi∂y^j(3)
不妨假设该样本的正确标签为 k k k ,即one-hot编码后的 y = [ y 1 , y 2 , … , y n ] y = [y_1, \ y_2, \dots, \ y_n] y=[y1, y2,…, yn] 中,只有 y k = 1 y_k = 1 yk=1 、其他 y j = 0 y_j= 0 yj=0 , 则 ( 3 ) (3) (3) 可以进一步化简为:
∂ L ∂ x i = − y k y ^ k ⋅ ∂ y ^ k ∂ x i ( 4 ) \frac{\partial L}{\partial x_i} = - \frac{y_k}{\hat{y}_k} \cdot \frac{\partial{\hat{y}_k}}{\partial x_i} \quad (4) ∂xi∂L=−y^kyk⋅∂xi∂y^k(4)
显然,接下来需要计算 ∂ y ^ k ∂ x k \frac{\partial{\hat{y}_k}}{\partial x_k} ∂xk∂y^k 。需要分两种情况:
- 当 i = k i = k i=k ,
∂ y ^ k ∂ x i = ∂ y ^ k ∂ x k = ∂ ( e x k ∑ j = 1 n e x j ) ∂ x k = e x k ( ∑ j = 1 n e x j ) − ( e x k ) 2 ( ∑ j = 1 n e x j ) 2 = e x k ∑ j = 1 n e x j − ( e x k ∑ j = 1 n e x j ) 2 = y ^ k − y ^ k 2 = y ^ k ( 1 − y ^ k ) ( 5 ) \begin{aligned} \frac{\partial{\hat{y}_k}}{\partial x_i} &= \frac{\partial{\hat{y}_k}}{\partial x_k} \\ &= \frac{\partial{(\frac{e^{x_k}}{\sum^{n}_{j=1} e^{x_j}}})}{\partial{x_k}} \\ &= \frac{e^{x_k}(\sum^{n}_{j=1}{e^{x_j}}) - (e^{x_k})^2}{(\sum^{n}_{j=1}{e^{x_j}})^2} \\ &= \frac{e^{x_k}}{\sum^{n}_{j=1} e^{x_j}} - (\frac{e^{x_k}}{\sum^{n}_{j=1}{e^{x_j}}})^2 \\ &= \hat{y}_k - {\hat{y}_k}^2 \\ &= \hat{y}_k(1 - \hat{y}_k) \end{aligned} \quad (5) ∂xi∂y^k=∂xk∂y^k=∂xk∂(∑j=1nexjexk)=(∑j=1nexj)2exk(∑j=1nexj)−(exk)2=∑j=1nexjexk−(∑j=1nexjexk)2=y^k−y^k2=y^k(1−y^k)(5)
- 当 i ≠ k i \neq k i=k ,
∂ y ^ k ∂ x i = ∂ ( e x k ∑ j = 1 n e x j ) ∂ x i = − e x k ⋅ e x i ( ∑ j = 1 n e x j ) 2 = − e x k ∑ j = 1 n e x j ⋅ e x i ∑ j = 1 n e x j = − y ^ k ⋅ y ^ i ( 6 ) \begin{aligned} \frac{\partial{\hat{y}_k}}{\partial x_i} &= \frac{\partial{(\frac{e^{x_k}}{\sum^{n}_{j=1} e^{x_j}}})}{\partial{x_i}} \\ &= \frac{-e^{x_k} \cdot e^{x_i}}{(\sum^{n}_{j=1}{e^{x_j}})^2} \\ &= - \frac{e^{x_k}}{\sum^{n}_{j=1} e^{x_j}} \cdot \frac{e^{x_i}}{\sum^{n}_{j=1}{e^{x_j}}} \\ &= - \hat{y}_k \cdot \hat{y}_i \end{aligned} \quad (6) ∂xi∂y^k=∂xi∂(∑j=1nexjexk)=(∑j=1nexj)2−exk⋅exi=−∑j=1nexjexk⋅∑j=1nexjexi=−y^k⋅y^i(6)
将 ( 5 ) , ( 6 ) (5), (6) (5),(6) 带入 ( 4 ) (4) (4) ,得:
∂ L ∂ x i = { − y k y ^ k ⋅ y ^ k ( 1 − y ^ k ) = − y k ( 1 − y ^ k ) = y ^ k − 1 , i = k − y k y ^ k ⋅ ( − y ^ k ⋅ y ^ i ) = y k ⋅ y ^ i = y ^ i , i ≠ k \frac{\partial L}{\partial x_i} = \begin{cases} {-} \frac{y_k}{\hat{y}_k} \cdot \hat{y}_k(1 - \hat{y}_k) = -y_k(1 - \hat{y}_k) = \hat{y}_k - 1, \quad i=k \\ {-} \frac{y_k}{\hat{y}_k} \cdot (-\hat{y}_k \cdot \hat{y}_i) = y_k \cdot \hat{y}_i = \hat{y}_i, \quad i \neq k \\ \end{cases} ∂xi∂L={−y^kyk⋅y^k(1−y^k)=−yk(1−y^k)=y^k−1,i=k−y^kyk⋅(−y^k⋅y^i)=yk⋅y^i=y^i,i=k
综上所述,可以得到Softmax层的反向传播公式为:
∂ L ∂ x = [ ∂ L ∂ x 1 … ∂ L ∂ x k … ∂ L ∂ x n ] = [ ∂ L ∂ x 1 … ∂ L ∂ x k … ∂ L ∂ x n ] = [ y ^ 1 … y ^ k − 1 … y ^ n ] \frac{\partial L}{\partial x} = \begin{bmatrix} \frac{\partial{L}}{\partial{x_1}} \\ \dots \\ \frac{\partial{L}}{\partial{x_k}} \\ \dots \\ \frac{\partial{L}}{\partial{x_n}} \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial{L}}{\partial{x_1}} \\ \dots \\ \frac{\partial{L}}{\partial{x_k}} \\ \dots \\ \frac{\partial{L}}{\partial{x_n}} \\ \end{bmatrix} = \begin{bmatrix} \hat{y}_1 \\ \dots \\ \hat{y}_k - 1 \\ \dots \\ \hat{y}_n \\ \end{bmatrix} ∂x∂L= ∂x1∂L…∂xk∂L…∂xn∂L = ∂x1∂L…∂xk∂L…∂xn∂L = y^1…y^k−1…y^n
由于 y k = 1 y_k = 1 yk=1 、其他 y i = 0 y_i = 0 yi=0 ,上式可以改写成:
∂ L ∂ x = [ y ^ 1 … y ^ k − 1 … y ^ n ] = [ y ^ 1 − y 1 … y ^ k − y k … y ^ n − y n ] = y ^ − y \frac{\partial L}{\partial x} = \begin{bmatrix} \hat{y}_1 \\ \dots \\ \hat{y}_k - 1 \\ \dots \\ \hat{y}_n \\ \end{bmatrix} = \begin{bmatrix} \hat{y}_1 - y_1 \\ \dots \\ \hat{y}_k - y_k \\ \dots \\ \hat{y}_n - y_n \\ \end{bmatrix} = \hat{y} - y ∂x∂L= y^1…y^k−1…y^n = y^1−y1…y^k−yk…y^n−yn =y^−y
代码层面, y ^ \hat{y} y^ 即Softmax输出的概率分布 probs 、 y y y 即真实标签的one-hot分布,考虑批次处理则结果还需除以 batch_size 。故可写出反向传播代码为:
def backward(self):grad_in = (self.probs - self.truth_onehot) / self.batch_sizereturn grad_in
整体实现
综上所述,Softmax层的整体代码实现为:
class Softmax:def __init__(self, device="cpu"):self.device = devicedef forward(self, x):x_max = torch.max(x, dim=1, keepdim=True) # 防止溢出,减去最大值来增加数值稳定性x_exp = torch.exp(x - x_max.values)self.probs = x_exp / torch.sum(x_exp, dim=1, keepdim=True)return self.probsdef cross_entropy(self, predictions, truths):probs = self.probs # Softmax得到的预测标签的概率分布# 设定一个最小值min_val,防止log(0)min_val = 1e-6probs = torch.where(probs < min_val, torch.full_like(probs, min_val), probs)# 计算交叉熵损失batch_size = predictions.shape[0]truth_onehot = torch.zeros(batch_size, probs.shape[1], device=self.device)truth_onehot[torch.arange(batch_size), truths] = 1loss = -torch.mean(torch.sum(truth_onehot * torch.log(probs), dim=1))self.batch_size = batch_size # 批次大小self.truth_onehot = truth_onehot # 真实标签的one-hot分布return lossdef backward(self):grad_in = (self.probs - self.truth_onehot) / self.batch_sizereturn grad_in
含单隐藏层的前馈神经网络(MLP)
由于上面已经实现了各组件的前向和反向传播方法,故实现模型时只需要按顺序将它们组合在一起即可:
class MLP:def __init__(self, input_size, hidden_size, output_size, device="cpu"):""" 初始化单隐藏层网络 """self.fc1 = MyLinear(input_size, hidden_size, device) # 输入到隐藏层的线性变换self.relu = ReLU() # 隐藏层激活函数self.fc2 = MyLinear(hidden_size, output_size, device) # 隐藏层到输出层的线性变换self.softmax = Softmax(device) # 输出层的 Softmax 激活def forward(self, x):""" 前向传播 """x = self.fc1.forward(x) x = self.relu.forward(x) x = self.fc2.forward(x) x = self.softmax.forward(x) return xdef backward(self):""" 反向传播 """grad = self.softmax.backward()grad = self.fc2.backward(grad)grad = self.relu.backward(grad)grad = self.fc1.backward(grad)def update(self, lr):""" 更新参数 """self.fc1.update(lr)self.fc2.update(lr)
训练评估
训练模型,并记录训练过程中模型在训练集和测试集上的损失进行可视化:
def train_and_evaluate(model, train_loader, test_loader, epochs, learning_rate):train_loss_history = []test_loss_history = []for epoch in range(epochs):total_loss = 0for images, labels in train_loader:probs = model.forward(images) # 前向传播loss = model.softmax.cross_entropy(probs, labels) # 计算损失model.backward() # 反向传播model.update(learning_rate) # 更新参数total_loss += loss.item()# 计算平均训练损失avg_train_loss = total_loss / len(train_loader)train_loss_history.append(avg_train_loss)# 评估模型在测试集上的准确率accuracy, avg_test_loss = evaluate(model, test_loader)test_loss_history.append(avg_test_loss)print(f"Epoch {epoch+1}/{epochs}, "f"Train Loss: {avg_train_loss:.4f}, "f"Test Accuracy: {(accuracy * 100):.4f}%")# 绘制曲线plt.figure(figsize=(10, 6))plt.plot(range(epochs), train_loss_history, label='Train Loss')plt.plot(range(epochs), test_loss_history, label='Test Loss')plt.xlabel('Epoch')plt.ylabel('Loss')plt.title('Training and Test Loss Curve')plt.legend()plt.grid(True)plt.show()def evaluate(model, test_loader):correct = 0total = 0total_test_loss = 0for images, labels in test_loader:probs = model.forward(images)loss = model.softmax.cross_entropy(probs, labels)total_test_loss += loss.item()# 获取预测的类别_, predicted = torch.max(probs, dim=1) # 输出每行最大值的索引,即预测的类别# 统计正确预测的数量correct += (predicted == labels).sum().item()total += labels.size(0) accuracy = correct / total # 计算准确率avg_test_loss = total_test_loss / len(test_loader)return accuracy, avg_test_loss
设定超参数,开始训练:
# 训练和评估
input_size = 784
hidden_size = 128
output_size = 10
n_epochs = 30
lr = 1e-2
batch_size = 64train_loader = MyDataLoader(train_set, batch_size, shuffle=True, device=my_device)
test_loader = MyDataLoader(test_set, batch_size, shuffle=False, device=my_device)model = MLP(input_size, hidden_size, output_size, my_device)train_and_evaluate(model=model,train_loader=train_loader,test_loader=test_loader,epochs=n_epochs,learning_rate=lr
)
上述初始超参数下,训练结果如下:

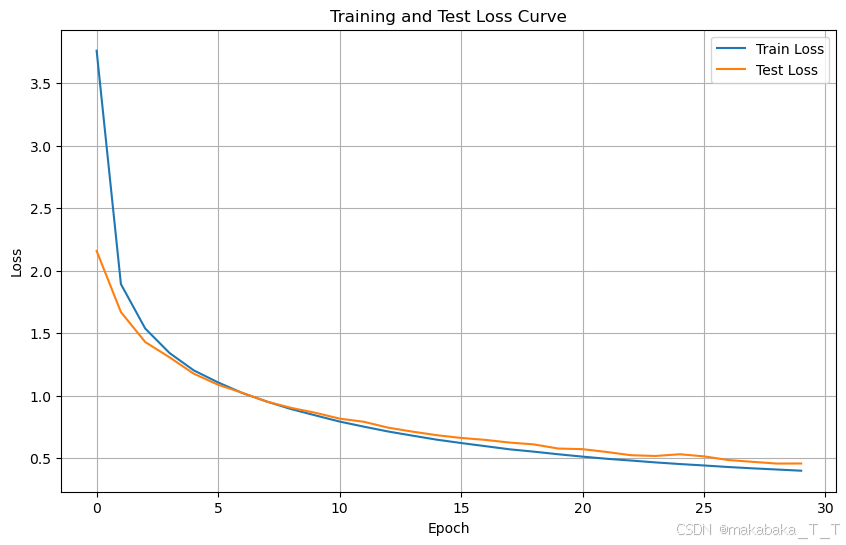
可以看到,最终准确率收敛在90%左右。为了提高准确率,尝试减小批次大小、增加隐藏层神经元个数、调整学习率等,部分实验结果如下:
hidden_size | lr | batch_size | n_epochs | 收敛准确率(±0.1%) |
|---|---|---|---|---|
| 128 | 0.01 | 64 | 30 | 90.3% |
| 256 | 0.01 | 64 | 30 | 92.8% |
| 512 | 0.01 | 64 | 30 | 93.7% |
| 512 | 0.001 | 32 | 30 | 91.3% |
| 512 | 0.02 | 32 | 20 | 95.1% |
| 512 | 0.05 | 16 | 20 | 95.7% |
| 1024 | 0.01 | 128 | 30 | 93.8% |
| 1024 | 0.1 | 16 | 20 | 96.5% |
本次实验中模型最好的分类准确度为96.5%左右:

相关超参数为:
hidden_size = 1024
n_epochs = 30
lr = 0.1
batch_size = 16
可以看到,由于本实验的数据集比较简单,将学习率设置得比较高(0.1)模型仍能收敛。
🔗 代码文件移步 我的代码仓库
相关文章:

手搓神经网络(MLP)解决MNIST手写数字识别问题 | 数学推导+代码实现 | 仅用numpy,tensor和torch基本计算 | 含正反向传播数学推导
手写数字识别(神经网络入门) 文章目录 手写数字识别(神经网络入门)实验概述实验过程数据准备模型实现线性变换层前向传播反向传播更新参数整体实现 激活函数层(ReLU)前向传播反向传播整体实现 Softmax层&am…...

esp32c3安装micropython环境
esp32c3竟然支持micropython环境,真的太让人高兴了。主要是python开发比较友好,开发速度要快于C和C, 可以用来快速创意验证。 下载 首先到官网:MicroPython - Python for microcontrollers 点击“download”进入下载页面&#…...

ES6的Iterator 和 for...of 循环
写在前面 在JavaScript中,Iterator(遍历器)是一种接口,用于遍历数据结构(如数组、对象等)中的元素。它提供了一种统一的方式来访问集合中的每个项,包括值和位置。 默认 Iterator 接口 许多内…...

《C语言程序设计现代方法》note-4 基本类型 强制类型转换 类型定义
文章目录 助记提要7章 基本类型7.1 整数类型有符号整数和无符号整数整数类型的说明符整数类型的范围整型常量整数溢出读/写整数 7.2 浮点类型浮点数的范围浮点常量读/写浮点数 7.3 字符类型字符被当做整数来操作转义序列大小写转换scanf和printf读/写字符getchar和putchar读写字…...
【数据类型 —— 数值类型】)
MySQL(4)【数据类型 —— 数值类型】
阅读导航 引言一、数据类型分类二、数值类型取值范围三、tinyint 类型1. 💻数值越界测试⭕有符号案例⭕无符号案例 四、bit 类型1. 基本语法2. 使用示例✅创建表并插入数据✅使用 BIT 存储多个设置✅查询和格式化 BIT 数据✅更新 BIT 数据 五、小数类型1. float&…...
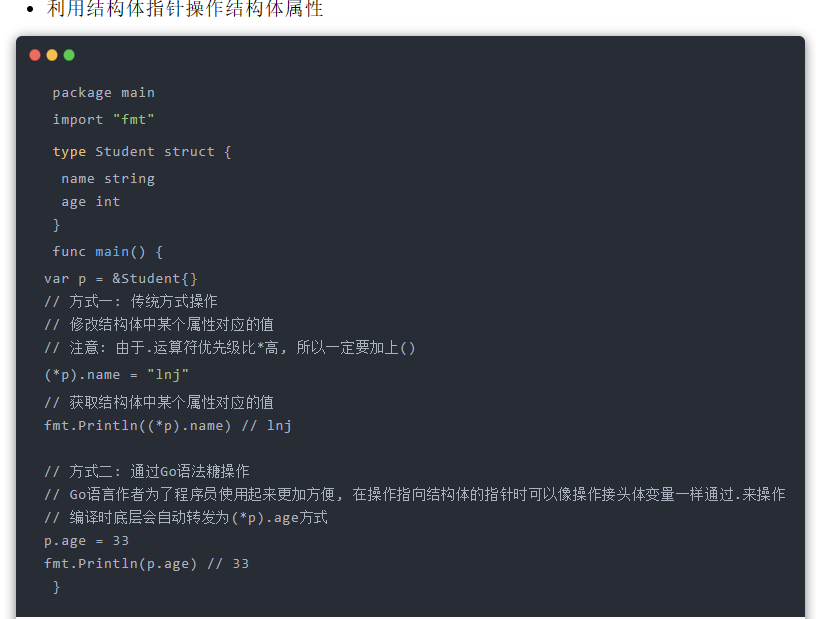
Golang超详细入门教程
Golang超详细入门教程 部分图片可能加载不出来,所以这里我上传到了自己的个人网站上也可以查看:http://dahua.bloggo.chat/testimonials/490.html 一、数据类型转换 C语言中数据可以隐式转换或显示转换, 但是Go语言中数据只能显示转换格式: 数据类型(…...

鸿蒙NEXT自定义组件:太极Loading
【引言】(完整代码在最后面) 本文将介绍如何在鸿蒙NEXT中创建一个自定义的“太极Loading”组件,为你的应用增添独特的视觉效果。 【环境准备】 电脑系统:windows 10 开发工具:DevEco Studio NEXT Beta1 Build Vers…...

FPGA 第7讲 简单组合逻辑译码器
时间:2024.11.15 一、学习内容 1.译码器 译码是编码的逆过程,在编码时,每一种二进制代码,都赋予了特定的含义,即都表示了一个确定的信号或者对象。把代码状态的特定含义翻译出来的过程叫做译码,实现译码操…...

opencv kdtree pcl kdtree 效率对比
由于项目中以一个环节需要使用kdtree ,对性能要求比较严苛,所以看看那个kdtree效率高一些。对比了opencv和pcl。 #include <array> #include <deque> #include <fstream> #include <opencv2/highgui.hpp> #include <opencv2/imgproc.hpp…...

1+X应急响应(网络)系统备份:
系统备份: 系统备份概述: 备份种类: 灾难恢复等级划分: 执行一次备份: 创建备份计划: 恢复备份:...
 详解)
python os.path.dirname(path) 详解
dirname 是一个用于处理文件路径的 Python 函数,通常用于获取给定路径的目录部分。它是 os.path 模块中的一部分。下面是对 dirname 函数的详细解释和使用示例。 1、导入模块 首先,你需要导入 os 模块,因为 dirname 是 os.path 模块的一部分…...

深度解析 Feign
一、引言 在当今微服务架构盛行的时代,众多微服务相互协作构成了复杂的分布式系统。然而,各个微服务之间的调用往往涉及到诸多繁琐的细节,比如网络请求的构建、参数的处理、响应的解析等。为了让开发人员能够更加专注于业务逻辑的实现&#x…...

AI工业大模型报告:体系架构、关键技术与典型应用
研究意义 随着新一代人工智能的发展, 大模型(如 GPT-4o 等)凭借大规模训练数据、网络参数和算 力涌现出强大的生成能力、泛化能力和自然交互能力, 展现出改变工业世界的巨大潜力. 尽管大模型 已在自然语言等多个领域取得突破性进展, 但其在工业应用中的…...

深入理解接口测试:实用指南与最佳实践5.0(五)
✨博客主页: https://blog.csdn.net/m0_63815035?typeblog 💗《博客内容》:.NET、Java.测试开发、Python、Android、Go、Node、Android前端小程序等相关领域知识 📢博客专栏: https://blog.csdn.net/m0_63815035/cat…...
)
常用List工具类(取交集、并集等等)
支持操作: 根据指定字段,获取两个对象集合的交集、补集、并集等将对象中的多个字段值,抽取到一个List中 import java.lang.reflect.Field; import java.util.*; import java.util.concurrent.ConcurrentHashMap; import java.util.function…...

4 C++ 复合类型:引用和指针
复合类型是指基于其它类型定义的类型。C 有几种复合类型,包括引用、指针。 1 引用 引用(reference)为对象起了另外一个名字,引用类型引用另外一种类型。通过将声明符写成&d的形式来定义引用类型,其中d是声明的变量…...

ABAP关于PS模块CJ20N中项目物料的屏幕和字段增强CI_RSADD
网上搜关于CJ20N的屏幕增强,基本都是关于项目定义(CI_PROJ)、项目WBS(CI_PRPS)、项目网络活动工序(CI_AFVU)的字段与屏幕增强,几乎没有关于项目物料(CI_RSADD)的字段屏幕增强,我在这里做一个分享。 主要逻辑:实现badi增强,并自建一个函数组后创建屏幕,在badi里面调用…...

探索IDE的无限可能:使用技巧与插件推荐
在软件开发的世界里,集成开发环境(IDE)是开发者的得力助手,它不仅提供了代码编辑、编译、调试等功能,还通过各种插件扩展了其功能,使得开发工作更加高效和便捷。本文将带你探索IDE的使用技巧和一些实用的插…...

自动化生成测试用例:利用OpenAI提升电商网站测试覆盖率
导语 自动化生成测试用例是软件测试领域一个强大的应用,通过OpenAI的语言模型,测试工程师可以快速生成高质量的测试用例,尤其是在处理边界条件和极端情况时,提升测试覆盖率。本篇文章将结合一个典型的电商网站案例,介绍…...

时间序列关于可解释性值得关注的论文汇总-第2篇
前言 这是时序可解释性论文汇总的第二篇,第一篇见这里(后台回复:“论文合集”可直接获取整理的文章)。深度学习的可解释性研究一直是热门,而时间序列的可解释性同样非常重要。这是因为时序模型被大量应用到特定领域&a…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
