若点集A=B则A必能恒等变换地变为B=A这一几何常识推翻直线(平面)公理
黄小宁
关键词:“更无理”复数
复平面z各点z的对应点z+1的全体是z+1面。z面平移变为z+1面就使x轴⊂z面沿本身平移变为u=x+1轴。R可几何化为R轴,R轴可沿本身平移变为R′轴,R′轴可沿本身平移变为R″轴,...。直线公理和平面公理使几百年解析几何一直认定这类平移变换是变回自己的变换。其实这是将无穷多各异直线(平面)误为同一线(面)的几百年重大错误。
数集相等的定义:若A(B)各元x(y)有与之对应相等的元y(x)∈B(A)即A各元与B各元可一一对应相等:x↔y=x(恒等对应、变换)则称A=B。若A=B则A必能(不是“只能”)恒等变换地变为B=A即必可有x↔y=x。
H定理:元点不少于两个的任何点集A平移非0距离变为B必≠A——推翻直线公理和平面公理。
证:点集A各点运动后还回到原位置的变换称为A的恒等变换。若A=B则A必可恒等变换地变为B=A,而在A 的各种平移中显然当且仅当平移的距离=0时才能是一种特殊的平移:恒等变换的平移。所以A平移非0距离变为B≌A中的A不可恒等变换地变为B——说明A≠B。在平移变换:x↔y=x+常数b(箭头两边的x是同一x)中显然当且仅当平移的距离|b|=0时才是恒等变换,即当且仅当b=0时各x与各对应y=x+b才能一一对应相等。证毕。
据H定理复平面z平移变为z+n面(≌z面)≠z面,其中常数n=1,2,3,…。中学的平面公理使数学一直误以为z+n面=z面。注:z+n面可平移变为(z+n)+n面;…。
可证明w=z+n面≌z面不是z面的任何真子集,w=z+n面≠z面且不是z面的任何真子集说明w=z+n面不能被z面包含而必有元点w=z+n“更无理”地突出在z面外。


相关文章:

若点集A=B则A必能恒等变换地变为B=A这一几何常识推翻直线(平面)公理
黄小宁 关键词:“更无理”复数 复平面z各点z的对应点z1的全体是z1面。z面平移变为z1面就使x轴⊂z面沿本身平移变为ux1轴。R可几何化为R轴,R轴可沿本身平移变为R′轴,R′轴可沿本身平移变为R″轴,...。直线公理和平面公理使几百年…...

网络安全之WINDOWS端口及病毒编写
目录 一、常见端口和服务 二、Windows病毒编写 声明:学习视频来自b站up主 泷羽sec,如涉及侵权马上删除文章 声明:本文主要用作技术分享,所有内容仅供参考。任何使用或依赖于本文信息所造成的法律后果均与本人无关。请读者自行判…...

Flink 开发工程应加载哪些依赖
在我们要开发Flink程序时,就会涉及到应该加载哪些Flink jar的问题。本章内容就是向你展示如何配置你的项目,添加必要的依赖。 每个应用程序都会依赖一些 Flink libraries,比如至少依赖 Flink APIs库,如果使用了connector,则还需要依赖connector相关的库,比如kafka、jdbc…...

wordpress建外贸独立站常用的多语言插件
WordPress是一个功能强大的内容管理系统,对于外贸独立站来说,多语言支持是非常重要的功能。以下是一些常用的WordPress多语言插件: 1. WPML (WordPress Multilingual) 这是最流行且功能最全面的多语言插件之一。它支持翻译整个网站…...

[SpB]如何开始使用 Spring Boot?
如何开始使用 Spring Boot? Spring Boot 简化了 Java 项目开发,你只需要专注于业务逻辑,底层的很多配置和功能由 Spring Boot 自动帮你处理。下面是你如何快速上手 Spring Boot 的步骤,以及如何通过 IDEA 了解 Spring Boot 的功能…...

蓝桥杯模拟
【问题描述】 如果一个数 p 是个质数,同时又是整数 a 的约数,则 p 称为 a 的一个质因数。 请问 2024 有多少个质因数。 【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只…...

数字化转型企业架构设计手册(交付版),企业数字化转型建设思路、本质、数字化架构、数字化规划蓝图(PPT原件获取)
1、企业架构现状分析 2、企业架构内容框架 3、企业架构设计方法 3.1 、业务架构设计方法 3.2 、数据架构设计方法 3.3 、应用架构设计方法 3.4 、技术架构设计方法 软件全套资料部分文档清单: 工作安排任务书,可行性分析报告,立项申请审批表&…...
)
2. langgraph中的react agent使用 (在react agent添加历史消息)
1. 导入必要的库 首先,我们需要导入所需的库。这里我们使用 langchain_openai 来与 智谱AI 模型进行交互,并使用 langchain_core.tools 来定义自定义工具。 from langchain_openai import ChatOpenAI from typing import Literal from langchain_core.…...

MySQL社区版的启动与连接
1.启动: 注意:MySQL是默认开机自启的 方式一: 1.WinR 的命令行中直接输入services.msc 2.在服务中找到数据库名称,然后鼠标右键点击启动 方式二: 1.在开始选项中搜索“cmd”命令提示符,使用管理员身份运行 …...

【图像压缩感知】论文阅读:Content-Aware Scalable Deep Compressed Sensing
tips: 本文为个人阅读论文的笔记,仅作为学习记录所用。本文参考另一篇论文阅读笔记 Title: Content-Aware Scalable Deep Compressed Sensing Journal: TIP 2022 代码链接: https://github.com/Guaishou74851/CASNet…...

物理hack
声明 声明 文章只是方便各位师傅学习知识,以下网站只涉及学习内容,其他的都与本人无关,切莫逾越法律红线,否则后果自负。 ✍🏻作者简介:致力于网络安全领域,目前作为一名学习者,很荣…...

Linux——环境基础开发工具使用2(正在更新中...)
1.自动化构建-make/Makefile 1.1 认识make和Makefile make是一个命令; Makefile是一个文件。 1.2 理解 其中在第一个图片中,第一行的 mytest:test.c 叫做依赖关系;第二行的 gcc test.c -o mytest 叫做依赖方法。 依赖关系和依赖方法共同…...

STM32传感器模块编程实践(十二) micro SD卡模块简介及驱动源码
文章目录 一.概要二.Micro SD卡模块主要特性三.Micro SD卡模块接线说明四.Micro SD卡模块参考原理图五.通讯协议介绍六.FATFS文件系统介绍七.STM32F030C8T6单片机与SD卡模块实现数据读写实验1.硬件准备2.软件工程3.软件主要代码4.实验效果 八.源代码工程下载九.小结 一.概要 M…...

Linux debian系统安装ClamTk开源图形用户界面(GUI)杀毒软件
一、ClamTk简介 ClamTk 是一个基于 ClamAV 的开源图形用户界面(GUI)杀毒软件。它使用 GTK2-Perl 脚本构建而成,支持32位与64位操作系统。ClamTk 提供了一个直观的用户界面,使得用户无需深入了解命令行即可完成大部分操作。它具备…...
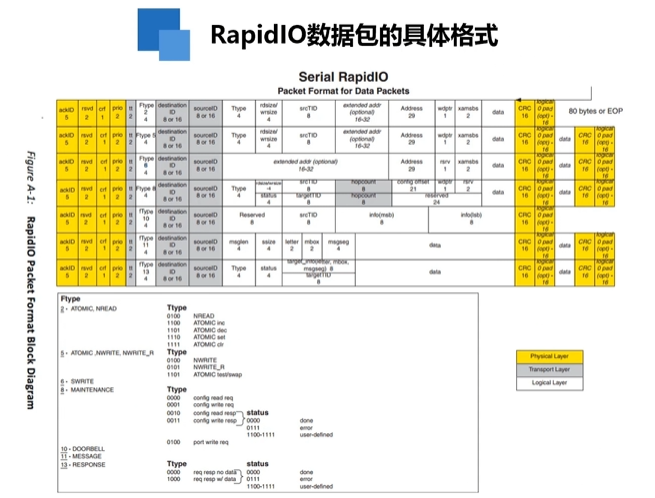
RapidIO介绍
传统串行总线(如 UART, SPI, I2C 等) 特点: 接口简单:传统的串行总线设计相对简单,通常使用少量的引脚,因此硬件设计较为简洁。协议简单:这些协议设计简单,容易实现,因…...

用魔方做存储器
用魔方模拟存储器是一种形象化的方式,特别适合教学演示或帮助理解存储器结构。以下是如何将魔方作为存储器的设计思路和可能的实现: 基本思路 魔方的结构: 魔方有 (6) 个面,每面 (3 \times 3 9) 个方块,总共 (6 \time…...

动力商城-03 Idea集成apifox Mybatis-Plus字段策略
1.Idea下载apifox插件 2.新建令牌放入Idea 3.右键上传到对应接口 4.设置前置url 插件能够自动识别swagger注解 Mybatis-Plus字段策略 1、FieldStrategy作用 Mybatis-Plus字段策略FieldStrategy的作用主要是在进行新增、更新时,根据配置的策略判断是否对实体对…...

python如何使用Rabbitmq
目录 一、Rabbitmq介绍 二、Rabbitmq的使用场景 1、异步处理 2、服务解耦 3、流量削峰 4、日志收集 5、发布订阅 6、任务调度 三、python如何使用Rabbitmq 1、安装依赖 2、基础使用 3、消息确认 4、消息持久化 5、公平调度 6、发布订阅 7、关键字发布 一、Rabbi…...

分布式,微服务,SpringCloudAlibaba,nacos,gateway,openFeign
想学习微服务SpringCloudAlibaba的小伙伴,可以观看视频 地址: https://www.bilibili.com/video/BV1cFDEYWEkY/?vd_source14d27ec13a4737c281b7c79463687112分布式架构和微服务是两个密切相关但又有所区别的概念。它们在现代软件工程中经常被提及&#…...

MySQL初学之旅(3)约束
目录 1.前言 2.正文 2.1约束类型 2.2NULL约束 2.3UNIQUE约束 2.4DEFAULT约束 2.5PRIMARY KEY主键约束 2.6FOREIGN KEY外键约束 2.7CHECK约束 3.小结 1.前言 哈喽大家好啊,今儿来继续给大家分享最近学习的MySQL和约束相关的知识点,希望大家一起…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
