多项式回归

以多元线性回归和特征工程的思想来想出一种称为多项式回归的新算法，它可以让您拟合曲线，非线性函数，您的数据。假设你有一个住房看起来像这样的数据集，其中特征x是以平方英尺为单位的大小。它看起来不像一条直线非常适合这个数据集。也许你想拟合一条曲线，也许是数据的二次函数，比如这包括大小x和y平方，这是大小提高到2的幂。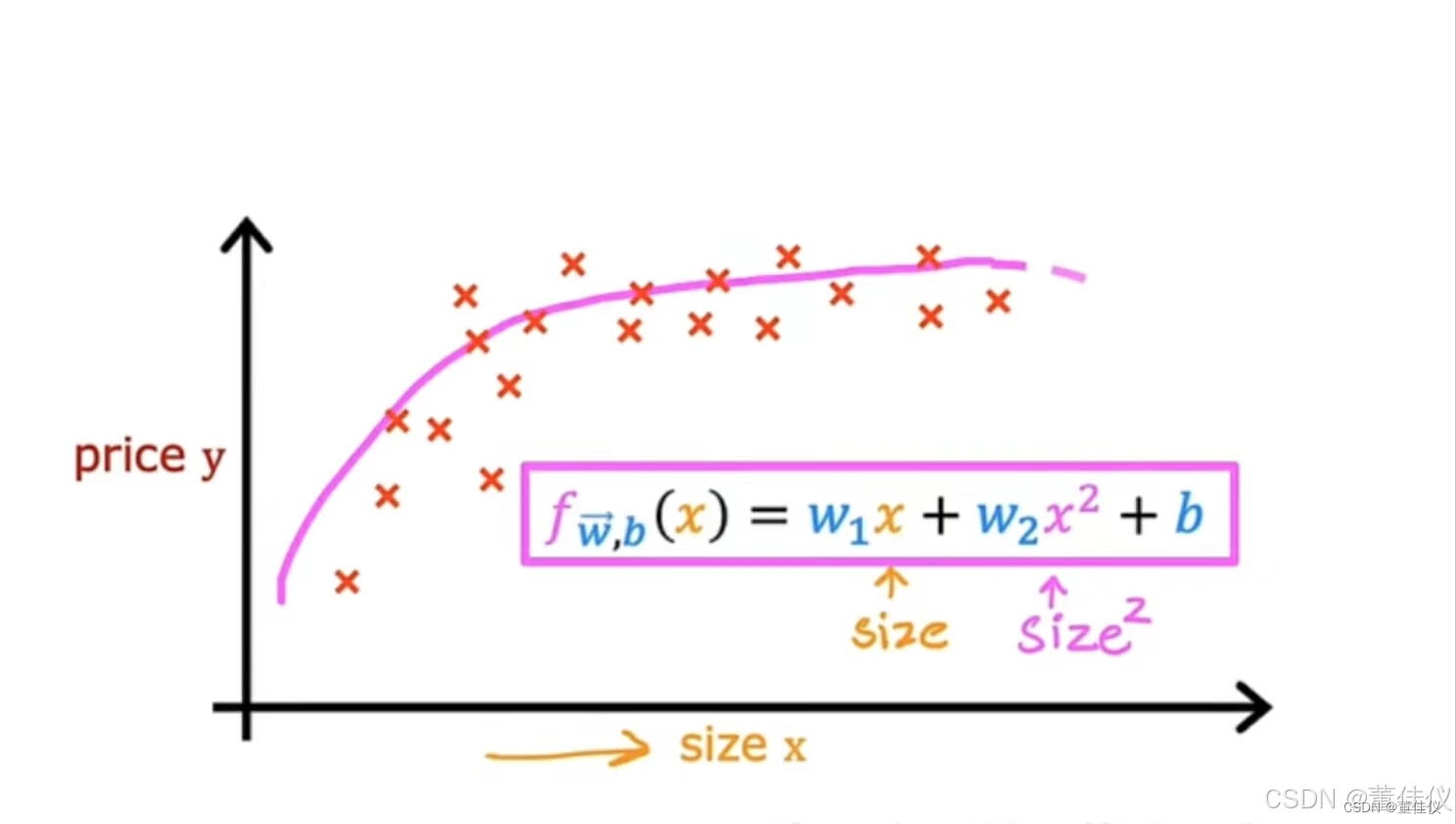也许这会让你更好的适应数据。但是你可能会认为你的二次模型没有真正意义因为二次函数最终会回归。当规模增加时，我们真的不会期望房价下跌。大房子似乎通常应该花费更多。然后你可以选择一个三次函数，我们现在不仅有x的平方还有x的立方。也许这个模型在这里产生了这条曲线，它更合适数据 

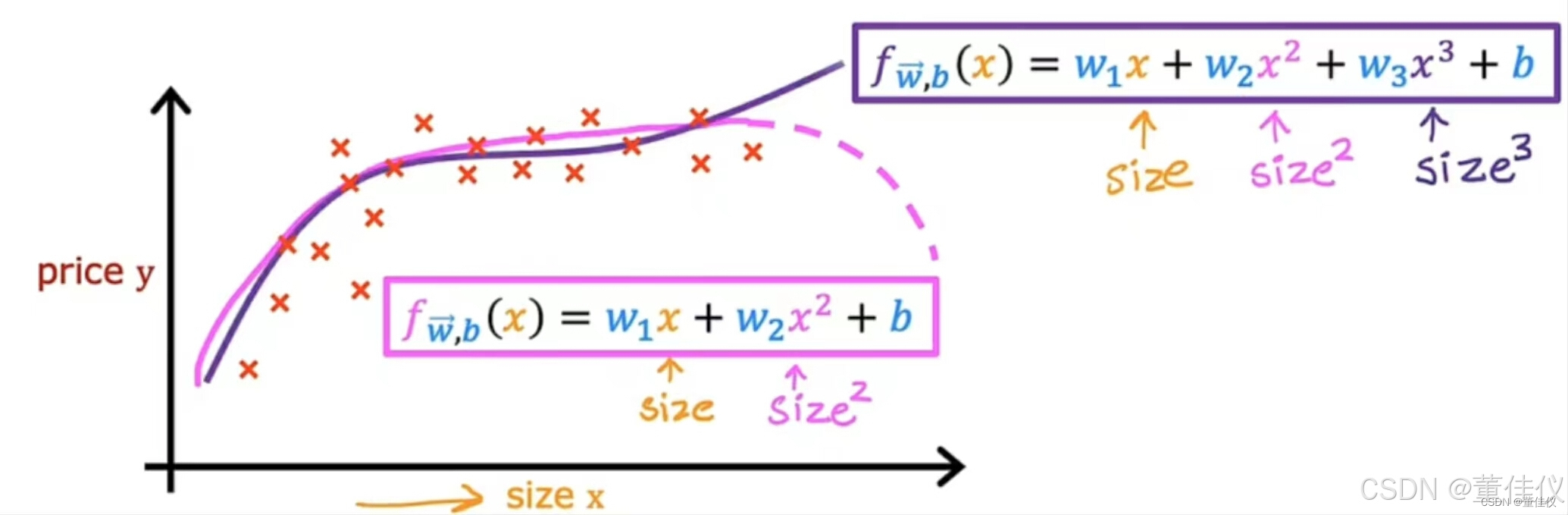因为大小最终会随着 大小的增加而恢复。这些都是多项式回归的例子，因为你选择了您的可选特征x，并将其提高到二或三或任何其他幂的幂。在三次函数的情况下，第一个特征是大小，第二个特征是大小的平方，第三个特征是大小的立方。如果你创建的功能是这些力量就像原来这样的平方的特征，那么特征缩放变得越来越重要。如果房子的大小不等，1-1000平方英尺，然后第二个特征，即大小的平方，范围从一到一百万，第三个特征，他的大小是立方的，范围从1到10亿这两个特征，x平方和x立方，具有非常不同的范围于原始特征x相比的值。如果你使用梯度下降，则应用特征缩放以获得，将您的特征转换为可比较的值范围。最后，只是最后一个示例，说明你如何真正拥有多种功能可供选择，另一种合理的替代方法是取大小的平方和size cubed就是说使用x的平方根。您的模型可能看起来像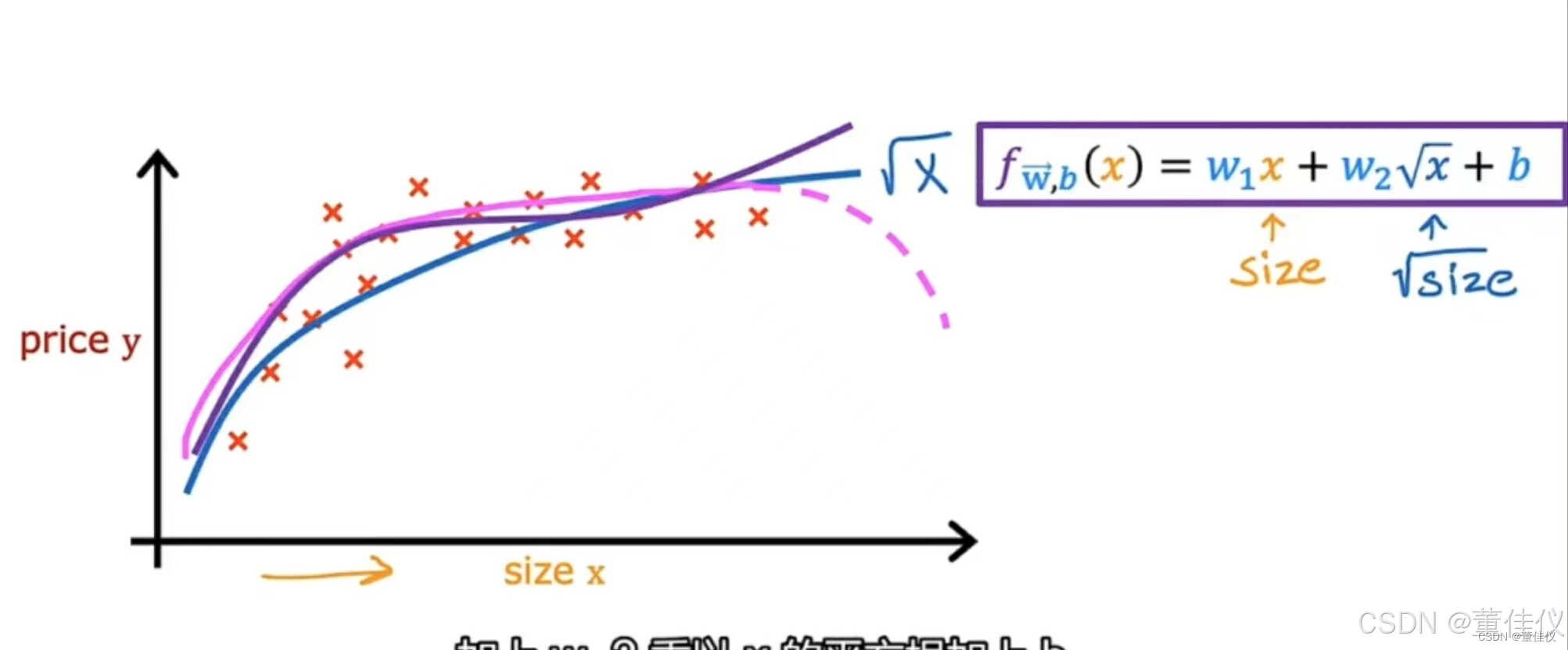这样，随后x的增加，她变得不那么陡峭，但他永远都不会变平而且他肯定永远不会回来。这将是另一种功能选择可能也适用于这个数据集。通过使用特征工程和多项式函数，你可以获得为了您的数据提供更好的模型。