蓝桥杯每日真题 - 第7天
题目:(爬山)
题目描述(X届 C&C++ B组X题)


解题思路:
-
前缀和构造:为了高效地计算子数组的和,我们可以先构造前缀和数组
a,其中a[i]表示从第 1 个元素到第i个元素的和。这样,对于任意区间[i, j]的子数组和,可以通过a[j] - a[i-1]快速得到。 -
枚举所有区间和:用双重循环枚举所有可能的区间
[i, j],将每个区间和存入multisets中。multiset支持快速查找、插入和删除,且自动排序,是处理该问题的合适选择。 -
最小差值的计算:
-
遍历每一个位置
i,将该位置作为第一个区间的右端点。 -
在
multiset中删除以i作为右端点的所有区间和,以避免区间重叠。 -
然后遍历每一个可能的左端点
j,计算第一个区间[j, i]的和k = a[i] - a[j-1]。 -
使用
lower_bound查找s中最接近k的区间和,计算绝对差值,并更新最小差值res。 -
在
lower_bound查找时,考虑s中前后两个元素,以确保找到最接近k的数值。
-
-
输出结果:最终输出最小的差值
res。
代码实现(C++):
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+10;
long long a[N];
int n;
multiset<long long>s;
long long minn(long long a,long long b){if(a<b) return a;else return b;
}
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);//取消同步流cin>>n;for(int i = 1;i<=n;i++) {cin>>a[i];a[i]+=a[i-1];//构造前缀和}for(int i = 1;i<=n;i++){for(int j = i;j<=n;j++){s.insert(a[j]-a[i-1]);//枚举右区间所有情况先加入set中}}long long res = 1e9;//这里的i是第一个区间的右端点for(int i = 1;i<n;i++){//删除掉以i作为右区间第一个数字的情况for(int j = i;j<=n;j++){
// auto p = s.find(a[j]-a[i-1]);
// s.erase(p);auto k = a[j] - a[i-1];s.erase(s.find(k));}//这里的j是第一个区间的左端点for(int j = 1;j<=i;j++){auto k = a[i] - a[j-1];//找到又区间中最接近k的位置,用lower_bound(s.begin(),s.end(),k)//会慢很多,不建议auto p = s.lower_bound(k);if(p!=s.end()){res = minn(res,abs(*p-k));}if(p!=s.begin()){p--;res = minn(res,abs(*p-k));//lower_bound返回的是第一个>=k的数字,因此绝对值最小的情况也可能在p前面一点}}}cout<<res<<endl;return 0;
}代码分析:
-
头文件和常量定义
-
引入头文件
#include <bits/stdc++.h>,方便使用标准库的各种数据结构和算法。 -
定义常量
N为数组的最大长度(设置为 1000)。 -
定义数组
a[N]用于存储前缀和,n表示元素数量。 -
使用
multisets存储所有子数组的和,支持排序和快速查找。
-
-
辅助函数
minn-
minn函数用于返回两个数中的较小值,这个函数会在更新最小差值时使用。 -
使用辅助函数代替
std::min可以提高代码可读性。
-
-
初始化和输入
-
ios::sync_with_stdio(0);、cin.tie(0);和cout.tie(0);是用于加快 I/O 操作的优化。 -
读取输入
n和数组元素,构造前缀和a[i] += a[i - 1];,a[i]表示从第一个元素到第i个元素的和。 -
构造前缀和后,可以通过
a[j] - a[i - 1]快速获得区间[i, j]的和。
-
-
枚举所有区间和并加入
multiset-
双重循环枚举所有可能的区间
[i, j]。 -
每个区间和通过
a[j] - a[i - 1]计算,并插入multisets中。 -
使用
multiset是因为它支持自动排序和快速查找最接近的值。
-
-
枚举区间、删除重叠区间和查找最小差值
-
外层循环的
i表示第一个区间的右端点。 -
内部循环先删除以
i为右端点的所有区间和,避免第一个区间和第二个区间重叠。 -
对于当前右端点
i,再枚举每个可能的左端点j,计算第一个区间[j, i]的和k = a[i] - a[j-1]。 -
使用
lower_bound查找s中最接近k的值。由于lower_bound返回的是第一个大于等于k的迭代器p,所以还需要检查p的前一个元素,以找到绝对差值最小的情况。 -
最小差值存储在
res中。
-
难度分析
⭐️⭐️⭐️⭐️
总结
-
使用前缀和快速计算子数组和。
-
使用
multiset存储所有子数组和,以支持有序查找和删除操作。 -
通过双重循环枚举区间和,并使用
lower_bound查找最接近的数值,从而找到两个不重叠子数组和之间的最小差值。
相关文章:

蓝桥杯每日真题 - 第7天
题目:(爬山) 题目描述(X届 C&C B组X题) 解题思路: 前缀和构造:为了高效地计算子数组的和,我们可以先构造前缀和数组 a,其中 a[i] 表示从第 1 个元素到第 i 个元素的…...

【Git】Git Clone 指定自定义文件夹名称:详尽指南
目录 引言一、git clone 基本语法二、默认行为:没有指定文件夹名称时三、如何指定自定义文件夹名称四、高级使用技巧:动态文件夹名称4.1 基于日期命名文件夹4.2 基于版本标签(Tag)动态命名文件夹4.1 基于日期命名文件夹4.2 基于版…...

终端快捷键学习笔记
以下是优化润色后的内容: 终端快捷键学习笔记 前言 终端(Terminal)是开发者、系统管理员以及技术人员常用的重要工具,它为我们提供了直接与操作系统交互的方式。不同操作系统中的终端使用体验存在差异,尤其在 Linux、…...
MySQL数据库的增删改查)
Go语言24小时极速学习教程(四)MySQL数据库的增删改查
通过前几篇想必你已经知道该如何使用Go语言写一些简单的程序了,那么从这一篇开始,我们开始探究如何用go语言能够写真正的企业级应用。第一步我们实现先能让程序对数据库进行增删改查,这里以MySQL为例。 1. 导入必要的包 首先需要导入databa…...

04 - Clickhouse-21.7.3.14-2单机版安装
目录 一、准备工作 1、确定防火墙处于关闭状态 2、CentOS 取消打开文件数限制 3、安装依赖 4、CentOS取消SELINUX 二、单机安装 2.1、下载安装 2.2、安装这4个rpm包 2.3、修改配置文件 2.4、启动服务 2.5、关闭开机自启 2.6、使用Client连接server 一、准备工作 1…...
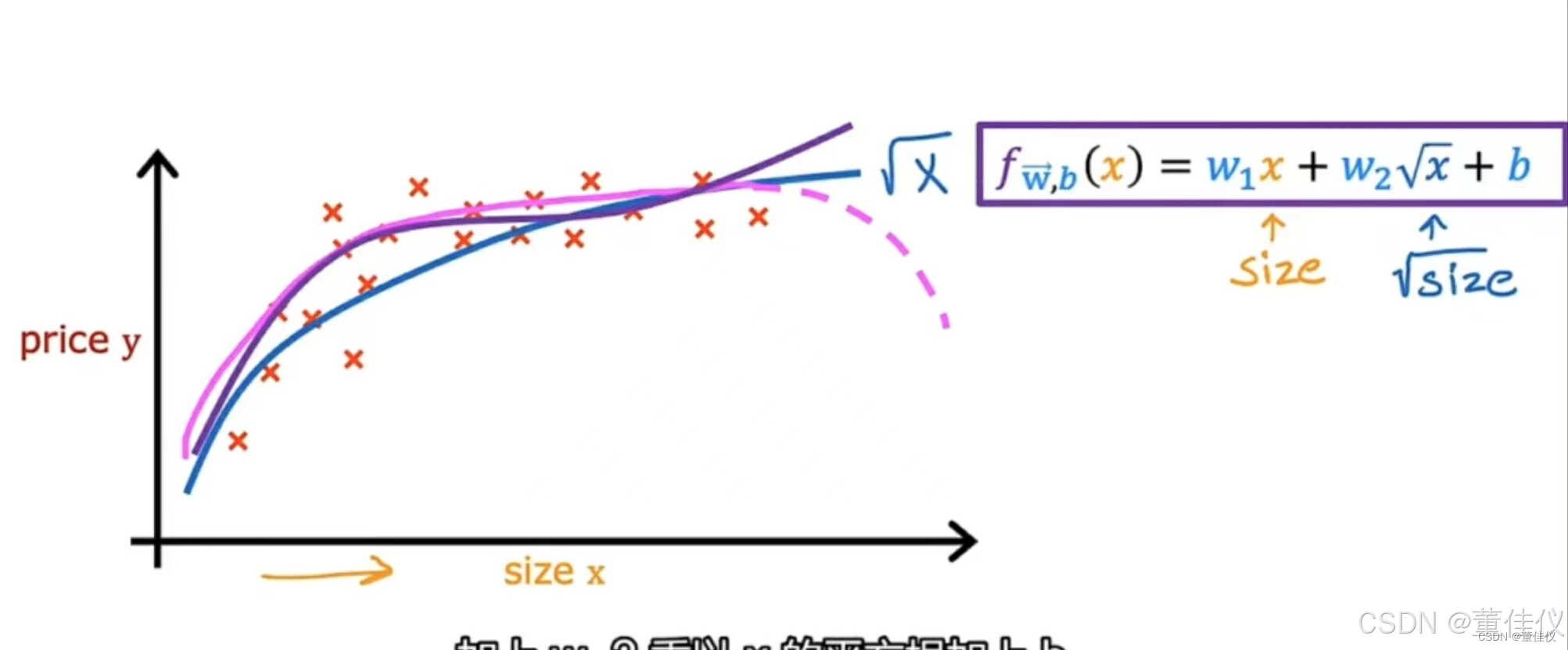
多项式回归
以多元线性回归和特征工程的思想来想出一种称为多项式回归的新算法,它可以让您拟合曲线,非线性函数,您的数据。假设你有一个住房看起来像这样的数据集,其中特征x是以平方英尺为单位的大小。它看起来不像一条直线非常适合这个数据集…...

vscode报错:Connecting with SSH time-out.
当我们在vscode上远程连接(Remote_SSH)Linux时,如果直接点关闭vscode,下次远程登陆后,就会弹出以下界面, 点击重新加载window就会弹出以下报错: 这是因为我们没有正常关闭remote-ssh, 导致linux上有多个vsc…...

python可视化将多张图整合到一起(画布)
这周有点事忙着,没时间重温刚结束的Mathurcup数学建模,这两天也是再看了下,论文还是赶紧挺烂的,但比国赛又有进步(说起国赛又不得不抱怨了,基本其余省份都发了,但江西......哎)。哎&…...

C函数如何返回参数lua使用
返回基本数据类型 数字类型(整数和浮点数) 在C函数中,可以使用lua_pushnumber函数将一个数字(整数或浮点数)压入Lua栈。当C函数返回后,Lua会从栈顶获取这个数字作为返回值。例如,以下是一个简单…...

pytest在conftest.py中实现用例执行失败进行截图并附到allure测试报告
conftest.py文件简介 conftest.py文件用于定义共享设置、夹具和钩子函数。 可以跨.py文件调用,有多个.py文件调用时,可让conftest.py只调用了一次fixture,或调用多次fixture; conftest.py与运行的用例要在同一个pakage下…...

编程之路,从0开始:数据在内存中的存储
目录 1、整数在内存中的存储 (1)大小端 (2)数据存储读取练习 2、浮点数在内存中的存储 Hello大家好,很高兴我们又见面啦!给生活添点Passion,开始今天的编程之路! 1、整数在内存中的存储 之…...

二叉树+树的OJ题讲解
求第K层节点个数 思路:走到K1就不走了,一次传回得到的值 #include<stdio.h> #include<stdlib.h> //树的定义 typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right; }BTNode;//手…...

信捷PLC转以太网连接电脑方法
信捷XC/XD/XL等系列PLC如何上下载程序?可以选择用捷米特JM-ETH-XJ模块轻松搞定,并不需要编程,即插即用,具体看见以下介绍: 产品介绍 捷米特JM-ETH-XJ是专门为信捷PLC转以太网通讯面设计,可实现工厂设备信息化需求,对…...
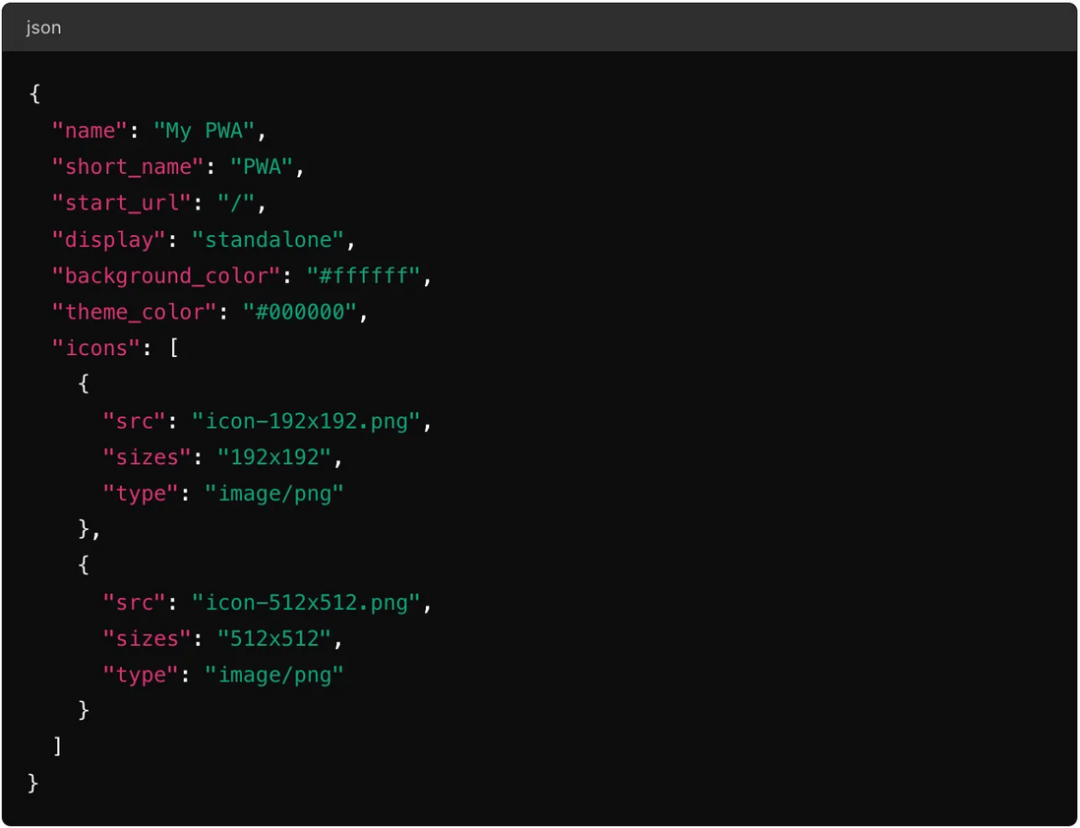
释放 PWA 的力量:2024 年的现代Web应用|React + TypeScript 示例
在2024年的Web开发领域,PWA(Progressive Web Apps)已经成为一个不可忽视的技术趋势。这篇文章将探讨PWA的最新发展,并通过实例展示如何构建一个现代PWA应用。 PWA的本质与优势 PWA本质上是一种将Web应用提升到接近原生应用体验的技…...

CVSS4与CVSS3的不同之二
在文章CVSS4与CVSS3的不同-CSDN博客中描述了CVSS3的缺点,以及CVSS4相对CVSS3做了哪些改进和带来了哪些优点。 但是具体CVSS4针对CVSS3做了哪些改动,还没有详细列举出来。 本文主要是针对CVSS4和CVSS的打分的大项和小项进行逐一对比,列出来具体…...

【Pip】如何清理 `pip` 包管理器 —— 完整指南
目录 引言1. 清理 pip 缓存2. 卸载不再需要的包2.1 如何查看已安装的包2.2 如何卸载不需要的包 3. 查看已安装的包及其依赖3.1 查看单个包的依赖3.2 查看所有包的依赖关系3.2 优化包依赖 4. 解决包冲突5. 合并和优化依赖5.1 优化 requirements.txt5.2 删除冗余依赖 6. pip 清理…...

操作数据库
""" 本文件是【连接数据库:通过链和代理查询鲜花信息】章节的配套代码,课程链接:https://juejin.cn/book/7387702347436130304/section/7388065974408183858 您可以点击最上方的“运行“按钮,直接运行该文件&…...

lua-lru缓存算法解析
lua-lru缓存算法解析 主要功能和作用1. 缓存管理:2. 数据存储与访问:3. 迭代器:4. 容量管理: 具体实现细节使用场景使用示例 lua-lru 是 Lua 语言中的一个 LRU(Least Recently Used,最近最少使用࿰…...

Python - 初识Python;Python解释器下载安装;Python IDE(一)
一、初识Python Python 是一种高级编程语言,Python是一种面向对象的解释型计算机程序设计语言,Python由荷兰国家数学与计算机科学研究中心的吉多范罗苏姆()Guido van Rossum吉多范罗苏姆()于1989 年底发明…...

鸿蒙学习基本概念
文章目录 1、当前移动应用开发中遇到的主要挑战包括:2、 新的应用生态应该具备如下特征:3、HarmonyOS 应用:使用 HarmonyOS SDK 开发的应用程序,能够在华为终端设备4、HarmonyOS 元服务:元服务是 HarmonyOS 面向万物互…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
