最短路径生成树的数量-黑暗城堡
信息学奥赛一本通T1486-黑暗城堡
时间限制: 2s 内存限制: 192MB 提交: 18 解决: 9
题目描述
知道黑暗城堡有 N 个房间,M 条可以制造的双向通道,以及每条通道的长度。
城堡是树形的并且满足下面的条件:
设 Di为如果所有的通道都被修建,第 i 号房间与第 1 号房间的最短路径长度;
而 Si 为实际修建的树形城堡中第 i 号房间与第 1号房间的路径长度;
要求对于所有整数 i(1≤i≤N),有 Si=Di成立。
你想知道有多少种不同的城堡修建方案。当然,你只需要输出答案对 231−1 取模之后的结果就行了。输入格式
第一行为两个由空格隔开的整数 N,M;
第二行到第 M+1 行为3 个由空格隔开的整数 x,y,l:表示 x 号房间与 y 号房间之间的通道长度为 l。输出格式
一个整数:不同的城堡修建方案数对 231−1 取模之后的结果。
样例输入
复制
4 6 1 2 1 1 3 2 1 4 3 2 3 1 2 4 2 3 4 1样例输出
复制
6提示
样例说明
一共有 4 个房间,6 条道路,其中 1 号和 2 号,1 号和 3 号,1 号和 4 号,2 号和 3 号,2 号和 4 号,3 号和 4 号房间之间的通道长度分别为 1,2,3,1,2,1。
而不同的城堡修建方案数对 231−1 取模之后的结果为 6。
数据范围:
对于全部数据,1≤N≤1000,1≤M≤N(N−1)/2,1≤l≤200。
题解:
思路为先用dijkstra求得1到各点最短路径,再依次通过dis[j]=dis[u]+w[i],即若该点的dis值加上到下一个点的权值等于下一个点的dis值,那么到下一个点的路径数加一。最后将所以的点的路径数相乘取mod即答案,注意取模时千万别用2e31-1,这个会有问题,直接用整型,别用浮点型,至于为什么希望有大佬帮忙回复一下,感谢。
#include<bits/stdc++.h> using namespace std; typedef pair<int, int>PII; const int N = 1010, M = N * N; const long long mod = (1<<31)-1; int h[N], e[M], ne[M], w[M], idx; int dis[N]; int cnt[N]; bool st[N]; int n, m;void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++; }void dij() {memset(dis, 0x3f, sizeof(dis));priority_queue<PII, vector<PII>, greater<PII>>q;q.push({ 0,1 });dis[1] = 0;while (q.size()) {auto t = q.top();q.pop();int u = t.second;if (st[u]) {continue;}st[u] = true;for (int i = h[u];~i;i = ne[i]) {int j = e[i];if (dis[j] > dis[u] + w[i]) {dis[j] = dis[u] + w[i];q.push({ dis[j],j });}}}} void get_cnt() {for (int u = 1;u <= n;u++) {for (int i = h[u];~i;i = ne[i]) {int j = e[i];if (dis[j] == dis[u] + w[i]) {cnt[j]++;}}} } long long get_ans() {long long ans = 1;cnt[1] = 1;for (int i = 1;i <= n;i++) {ans *= cnt[i];ans %= mod;}return ans; } int main() {cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1;i <= m;i++) {int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);}dij();get_cnt();long long res = get_ans();cout << res; }
相关文章:

最短路径生成树的数量-黑暗城堡
信息学奥赛一本通T1486-黑暗城堡 时间限制: 2s 内存限制: 192MB 提交: 18 解决: 9 题目描述 知道黑暗城堡有 N 个房间,M 条可以制造的双向通道,以及每条通道的长度。 城堡是树形的并且满足下面的条件: 设 Di为如果所有的通道都被修建…...

将已有的MySQL8.0单机架构变成主从复制架构
过程: 把数据库做一个完全备份, 恢复到从节点上, 恢复后从备份的那个点开始往后复制,从而保证后续数据的一致性。 步骤: 修改 master 主节点 的配置( server-id log-bin )master 主节点 完全备份( mysqldump )master 主节点 创建…...

JSON.stringify的应用说明
前言 JSON.stringify() 方法将 JavaScript 对象转换为字符串,在日常开发中较常用,但JSON.stringify其实有三个参数,后两个参数,使用较少,今天来介绍一下后两个参数的使用场景和示例。 语法及参数说明 JSON.stringify()…...
)
pyflink datastream数据流ds经过一系列转换后转为table,t_env.from_data_stream(ds)
在 pyflink 处理数据流过程中,有时候需要将data_stream转为table,下面是正确的方式,即每一个算子(map,reduce, window)操作之后需要指定输出数据类型。 from pyflink.common.typeinfo import Types from pyflink.datastream import StreamEx…...

vxe-grid table 校验指定行单元格的字段,只校验某个列的字段
Vxe UI vue vxe-table 中校验表格行是非常简单的,只需要配置好校验规则,然后调用 validate 方法就可以自动完成校验,但是由于项目淡色特殊需求,在某个单元格的值修改后需要对另一个列的值就行校验,这个时候又不需要全部…...
)
【Java多线程】单例模式(饿汉模式和懒汉模式)
目录 单例模式的定义: 饿汉式--单例模式 定义: 案例: 优缺点: 懒汉式--单例模式: 定义: 1)懒汉式单例模式(非线程安全) 2)线程安全的懒汉式单例模…...

python 异步编程之协程
最近在学习python的异步编程,这里就简单记录一下,免得日后忘记。 首先,python异步实现大概有三种方式,多进程,多线程和协程;多线程和多进程就不用多说了,基本上每种语言都会有多进行和多线程的…...

现代密码学|古典密码学例题讲解|AES数学基础(GF(2^8)有限域上的运算问题)| AES加密算法
文章目录 古典密码凯撒密码和移位变换仿射变换例题多表代换例题 AES数学基础(GF(2^8)有限域上的运算问题)多项式表示法 | 加法 | 乘法X乘法模x的四次方1的乘法 AES加密算法初始变换字节代换行移位列混合轮密钥加子密钥(…...

算法沉淀一:双指针
目录 前言: 双指针介绍 对撞指针 快慢指针 题目练习 1.移动零 2.复写零 3.快乐数 4.盛水最多的容器 5.有效三角形的个数 6.和为s的两个数 7.三数之和 8.四数之和 前言: 此章节介绍一些算法,主要从leetcode上的题来讲解ÿ…...
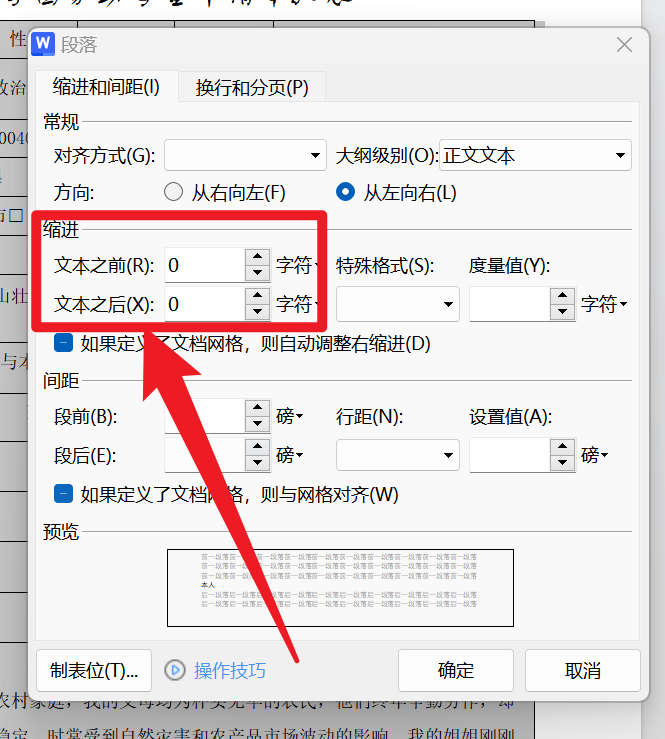
Word_小问题解决_1
1.第二页是空白的,但是删不掉 将鼠标弄到第二页最开始的地方打开段落设置行距为固定值0.7磅 2.表格中有文字进入了表格中怎么办 打开段落,将缩进改为0即可...

基于opencv制作GUI界面
可以基于cvui头文件实现一些控件操作,头文件及demo实例 这是一个demo main.cpp #include <opencv2/opencv.hpp> #define CVUI_IMPLEMENTATION #include "cvui.h"#define WINDOW_NAME "CVUI Hello World!"int main(void) {cv::Mat frame…...

微服务即时通讯系统的实现(客户端)----(2)
目录 1. 将protobuf引入项目当中2. 前后端交互接口定义2.1 核心PB类2.2 HTTP接口定义2.3 websocket接口定义 3. 核心数据结构和PB之间的转换4. 设计数据中心DataCenter类5. 网络通信5.1 定义NetClient类5.2 引入HTTP5.3 引入websocket 6. 小结7. 搭建测试服务器7.1 创建项目7.2…...

QT使用libssh2库实现sftp文件传输
本篇文章通过用户名和密码来连接服务器端,通过密匙连接服务器端可以参考另外一篇文章: https://blog.csdn.net/u012372584/article/details/143826199?sharetype=blogdetail&sharerId=143826199&sharerefer=PC&sharesource=u012372584&spm=1011.2480.3001.…...

【Linux】进程的优先级
进程的优先级 一.概念二.修改优先级的方法三.进程切换的大致原理:四.上下文数据的保存位置: 一.概念 cpu资源分配的先后顺序,就是指进程的优先权(priority)。 优先权高的进程有优先执行权利。配置进程优先权对多任务环…...

python实现十进制转换二进制,tkinter界面
目录 需求 效果 代码实现 代码解释 需求 python实现十进制转换二进制 效果 代码实现 import tkinter as tk from tkinter import messageboxdef convert_to_binary():try:# 获取输入框中的十进制数decimal_number int(entry.get())# 转换为二进制binary_number bin(de…...

电子应用设计方案-12:智能窗帘系统方案设计
一、系统概述 本设计方案旨在打造便捷、高效的全自动智能窗帘系统。 二、硬件选择 1. 电机:选用低噪音、扭矩合适的智能电机,根据窗帘尺寸和重量确定电机功率,确保能平稳拉动窗帘。 2. 轨道:选择坚固、顺滑的铝合金轨道&…...

力扣 回文链表-234
回文链表-234 const int N 1e55; int a[N];//定义一个整形的全局数组作为辅助数组存储链表反转前的值 class Solution { /*本题的解题思路是先将链表中每个值存储到辅助数组a中,然后反转链表, 最后,反转后链表的值和没反转之前的值…...

采样率22050,那么CHUNK_SIZE 一次传输的音频数据大小设置多少合适?unity接收后出现卡顿的问题的思路
在采样率为22050的情况下,选择合适的 CHUNK_SIZE 主要取决于 Unity 接收和处理音频数据的效率。以下是设置 CHUNK_SIZE 的一些建议: 计算 CHUNK_SIZE:音频的传输数据量可以通过公式 CHUNK_SIZE 采样率 * 传输间隔秒数 * 每样本字节数 * 声道…...

网络初识--Java
一、网络通信基础 1.IP地址 IP地址主要⽤于标识⽹络主机、其他⽹络设备(如路由器)的⽹络地址。简单说,IP地址⽤于定位主 机的⽹络地址。 就像我们发送快递⼀样,需要知道对⽅的收货地址,快递员才能将包裹送到⽬的地。…...

K8S单节点部署及集群部署
1.Minikube搭建单节点K8S 前置条件:安装docker,注意版本兼容问题 # 配置docker源 wget https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo -O /etc/yum.repos.d/docker-ce.repo# 安装docker环境依赖 yum install -y yum-utils device-m…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
