The 3rd Universal CupStage 15: Chengdu, November 2-3, 2024(2024ICPC 成都)
Problem L. Recover Statistics
题目意思:
给定a, b, c三个值,确保构造的数列中包含满足题目的数量
解题思路:
100 中 选择a 50个, b45个, c4个。
#include <iostream>using namespace std;using ll = long long;int main(){ios::sync_with_stdio(0);cin.tie(0);int a, b, c;cin >> a >> b >> c;cout << 100 << endl;for(int i = 0; i < 50; i ++)cout << a << " ";for(int i = 0; i < 45; i ++)cout << b << " ";for(int i = 0; i < 4; i ++)cout << c << " "; cout << c + 1;return 0;
}Problem A. Arrow a Row
题目意思:
n次操作,构造出给定字符串,每次操作可以覆盖之前的操作。
解题思路:
每次把一个字符变为满足题意的字符,n次之内操作就可以完成构造
#include <iostream>
#include <string>
#include <vector>using namespace std;void solve(){string s;cin >> s;int len = s.size();if(len < 5 || s[0] == '-'){cout << "No\n";return ;}for(int i = len - 1; i >= len - 3; i --){if(s[i] == '-'){cout << "No\n";return ;}}int f = 0;for(int i = 0; i < len; i ++){if(s[i] == '-')f = 1;}if(f == 0){cout << "No\n";return ;}vector<pair<int, int>> res;int end = len - 1;for(int i = len - 3; i >= 0; i --){if(s[i] == '>'){res.push_back({1, end + 1});end --;}elsebreak;}end ++;for(int i = 1; i < end - 3; i ++){if(s[i] == '>')res.push_back({i + 1, end - i + 1});}if(res.size() <= len){cout << "Yes ";cout << res.size() << endl;for(auto [x, y] : res)cout << x << " " << y << endl;}elsecout << "No\n";
}int main(){ios::sync_with_stdio(0);cin.tie(0);int n;cin >> n;while(n --){solve();}return 0;
}Problem G. Expanding Array
题目意思:
每次在相邻的两个数之间做运算,再将新构成的数插入到两数之间,再次做一样的运算,可做无限次运算,问最多能构成多少个不同的数。
解题思路:
利用等式 a ^ b = c => b = a ^ c, 通过这条性质可以无线构造出相邻的.
a & ( a ^ b ) ^ a = a & a ^ (a & b ) ^ a = a & b
0 ^ x = x
#include<iostream>
#include<vector>
#include<set>using namespace std;using ll = long long;int main(){ios::sync_with_stdio(0);cin.tie(0);int n;cin >> n;vector<int> a(n);set<int> cnt;for(auto &x : a) cin >> x;for(int i = 0; i < n - 1; i ++){cnt.insert(a[i]);int t1 = a[i] | a[i + 1];int t2 = a[i] & a[i + 1];int t3 = a[i] ^ a[i + 1];int t4 = t1 ^ a[i];int t5 = t1 ^ a[i + 1];cnt.insert(t1); cnt.insert(t2);cnt.insert(t3);cnt.insert(t4);cnt.insert(t5);}cnt.insert(0);cnt.insert(a[n - 1]);cout << cnt.size() << endl;return 0;
}Problem B. Athlete Welcome Ceremony
题目意思:
给定一个字符串和a, b, c的数量,问能构成多少种不同的长度为x的序列。
解题思路:
计数dp.
由于题目范围很小,我们很显然可以枚举所有满足cnt个问号,abc的数量,根据题目限制,相邻的两个字符不能相同。状态定义为dp[x][y][z][p],1 - i 中以p结尾的字符,并且保证当前的和上一层的不重复。我们可以用滚动数组来实现。
对于每次询问,我们直接找出f[x][y][z]即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
#define pb push_back
#define vi vector<int>
#define vii vector<pair<int, int>>
#define ff first
#define ss second
// ++ ~! */+- <<>> <> == &^| &&|| =int dp[310][310][310][3]; // ijkz 对前i个字符,使用了j个a字符,k个b字符,第i个字符是 z + 'a'的方案数
int f[310][310][310]; // 有i个a,j个b,k个c的方案数void solve()
{int n, m;cin >> n >> m;string s;cin >> s;s = ' ' + s;vector<int> cnt(n + 1);for (int i = 1; i <= n; i++)cnt[i] = cnt[i - 1] + (s[i] == '?');// 先初始化一下方案数if (s[1] == '?')dp[1][1][0][0] = dp[1][0][1][1] = dp[1][0][0][2] = 1;elsedp[1][0][0][s[1] - 'a'] = 1;for (int i = 2; i <= n; i++){for (int ca = 0; ca <= cnt[i]; ca++){for (int cb = 0; cb + ca <= cnt[i]; cb++){if (s[i] != '?'){int num = dp[i - 1][ca][cb][0] + dp[i - 1][ca][cb][1] + dp[i - 1][ca][cb][2]; //上一层总方案数dp[i][ca][cb][s[i] - 'a'] = (num - dp[i - 1][ca][cb][s[i] - 'a']) % mod; // 去掉上一层一样的,其他结尾字母为0continue;}if (ca){int num = dp[i - 1][ca - 1][cb][1] + dp[i - 1][ca - 1][cb][2]; dp[i][ca][cb][0] = num % mod;}if (cb){int num = dp[i - 1][ca][cb - 1][0] + dp[i - 1][ca][cb - 1][2];dp[i][ca][cb][1] = num % mod;}if (cnt[i] - ca - cb){int num = dp[i - 1][ca][cb][0] + dp[i - 1][ca][cb][1];dp[i][ca][cb][2] = num % mod;}}}}// 先获得特定i j k对应的方案数for(int i = 0; i <= cnt[n]; i ++) for (int j = 0; i + j <= cnt[n]; j++){int num = dp[n][i][j][0] + dp[n][i][j][1] + dp[n][i][j][2];f[i][j][cnt[n] - i - j] = num % mod; }// 获得i j k有富余的情况对应的方案数 三维前缀和for (int i = 0; i <= 300; i++) {for (int j = 0; j <= 300; j++) {for (int k = 0; k <= 300; k++) {if (i > 0) f[i][j][k] += f[i - 1][j][k];if (j > 0) f[i][j][k] += f[i][j - 1][k]; if (k > 0) f[i][j][k] += f[i][j][k - 1]; if (i && j)f[i][j][k] += mod - f[i - 1][j - 1][k];if (k && j)f[i][j][k] += mod - f[i][j - 1][k - 1];if (i && k)f[i][j][k] += mod - f[i - 1][j][k - 1];if (i && j && k)f[i][j][k] += f[i - 1][j - 1][k - 1];f[i][j][k] %= mod;}}}while (m --) {int x, y, z; cin >> x >> y >> z;cout << f[x][y][z] << '\n';}
}signed main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t = 1;//cin >> t;while (t--) solve();return 0;
}
/* /\_/\
* (= ._.)
* / > \>
*/Problem I. Good Partitions
题目意思:
给定一个数组,平均分割k段,每一段保证相邻的两个元素不是递增的,求满足条件的k。
同时可以单点修改,再p位置修改为v。
解题思路:
1.满足条件的分割点就是if(a[i] > a[i + 1])那么i就是分割点。
2.求出分割点的gcd,找出他因子的个数,就是分割方法的总数。
3.为了支持单点修改,每次修改完会有4种结果,并且只会对位置p之后的结果会有影响,我们用线段树来维护即可。
#include<bits/stdc++.h>using namespace std;using ll = long long;
using ld = long double;
using pii = pair<int, int>;
using ull = unsigned long long;struct node{int l, r;ll val;
};
const int N = 2e5 + 10;
int cnt[N];
int gcd(ll a, ll b)
{return b ? gcd(b, a % b) : a;
}class SegmentTree {public:int n;vector<node> c;vector<int> a;
public:SegmentTree (int x){n = x << 2;c.resize(n);a.resize(x + 1);}void build(int k, int l, int r){c[k] = {l, r, 0};if(l != r){int mid = (l + r) / 2;build(k << 1, l, mid);build(k << 1 | 1, mid + 1, r);}}void pushup(int k){c[k].val = gcd(c[k << 1].val, c[k << 1 | 1].val);}void modify(int k, int x, int v){if(c[k].l == c[k].r) c[k].val = v;else{int mid = c[k].l + c[k].r >> 1;if(x <= mid ) modify(k << 1, x, v);else modify(k << 1 | 1, x, v);pushup(k);}}
};void solve(){int n, m;cin >> n >> m;SegmentTree s(n);s.build(1, 1, n);for(int i = 1; i <= n; i ++){cin >> s.a[i];}for (int i = 1; i < n; i++){if (s.a[i] > s.a[i + 1]) s.modify(1, i, i);else s.modify(1, i, 0);}int ans = s.c[1].val;if(ans == 0) cout << n << endl;else cout << cnt[ans] << endl;int p, v;while(m --){cin >> p >> v;s.a[p] = v;if(s.a[p - 1] > s.a[p]) s.modify(1, p - 1, p - 1);else s.modify(1, p - 1, 0);if(p < n){if(s.a[p] > s.a[p + 1]) s.modify(1, p, p);else s.modify(1, p, 0);}int ans = s.c[1].val;if(ans == 0) cout << n << endl;else cout << cnt[ans] << endl;}
}int main(){ios::sync_with_stdio(0);cin.tie(0);for (int i = 1; i <= 200001; i++)for (int j = 1; j * i <= 200001; j++)cnt[i * j] ++;int t = 1;cin >> t;while(t --)solve();return 0;
}Problem J. Grand Prix of Ballance
签到模拟
相关文章:
)
The 3rd Universal CupStage 15: Chengdu, November 2-3, 2024(2024ICPC 成都)
Problem L. Recover Statistics 题目意思: 给定a, b, c三个值,确保构造的数列中包含满足题目的数量 解题思路: 100 中 选择a 50个, b45个, c4个。 #include <iostream>using namespace std;using ll long …...

显示微服务间feign调用的日志
第一步 package com.niuniu.common.config;import com.niuniu.common.CommonConstant; import com.niuniu.common.utils.UserContext; import feign.Logger; import feign.RequestInterceptor; import feign.RequestTemplate; import org.springframework.context.annotation.…...

SOHO场景开局(小型,多子网):AP+管理型交换机+路由器+光猫
业务需求 1. 实现除光猫外,整网设备通过APP进行开局,开局部署完成后,能够通过APP远程运维。 2. 需要单独划分访客、办公、视频监控3个子网,其中访客子网供顾客无线上网使用,办公子网用于接入无线和有线办公终端&#x…...
Android - Pixel 6a 手机OS 由 Android 15 降级到 Android 14 操作记录
Pixel 6a 手机由 Android 14 升级到 Android 15了,但是由于一些原因又想降级回 Android 14, 能降吗?该怎么降级呢?本篇文章来记述实际操作过程,希望能给想做相同操作的人一些帮助。 答案当然是能降,而且我…...

linux系统kkFileView 配置https预览文件
思路: 1.kkfile的 context全局路径可以修改 context-path,比如:server.servlet.context-path 2.使用nginx反向代理 /kkfile 转发到 kkfile路径上 官网教程 kkFileView - 在线文件预览 1、配置config/application.properties. server.se…...

stm32——通用定时器时钟知识点
(该图来自小破站 铁头山羊老师的stm32标准库教学)...

前端无感刷新token
摘要: Axios 无感知刷新令牌是一种在前端应用中实现自动刷新访问令牌(access token)的技术,确保用户在进行 API 请求时不会因为令牌过期而中断操作 目录概览 XMLHttpRequestAxiosFetch APIJQuni.request注意事项: 访问…...

针对股票评论的情感分类器
🏡作者主页:点击! 🤖编程探索专栏:点击! ⏰️创作时间:2024年11月16日13点39分 神秘男子影, 秘而不宣藏。 泣意深不见, 男子自持重, 子夜独自沉。 论文链接 点击开启你的论文编程之旅…...

Day18 Nim游戏
你和你的朋友,两个人一起玩 Nim 游戏: 桌子上有一堆石头。 你们轮流进行自己的回合, 你作为先手 。 每一回合,轮到的人拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。 假设你们每一步都是最优解。请编写一个函数ÿ…...
理解反射,学会反射:撬开私有性质(private)的属性与方法
看到这句话的时候证明:此刻你我都在努力 加油陌生人 个人主页:Gu Gu Study专栏:用Java学习数据结构系列喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹喜欢的话可以点个赞谢谢了。作者:小…...
Redis在高性能缓存中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 Redis在高性能缓存中的应用 Redis在高性能缓存中的应用 Redis在高性能缓存中的应用 引言 Redis 概述 定义与原理 发展历程 Redi…...

菲涅耳全息图
菲涅耳全息图:记录介质在物光波场的菲涅耳衍射区(物体到记录介质表面的距离在菲涅耳衍射区内)。 一、点源全息图的记录和再现 1.1 记录 设物光波和参考光波是从点源O(xo, yo, zo)和点源 R(xr, yr, zr)发出的球面波, 波长为λ1, 全息底片位于z0 的平面上, 与两个点源…...
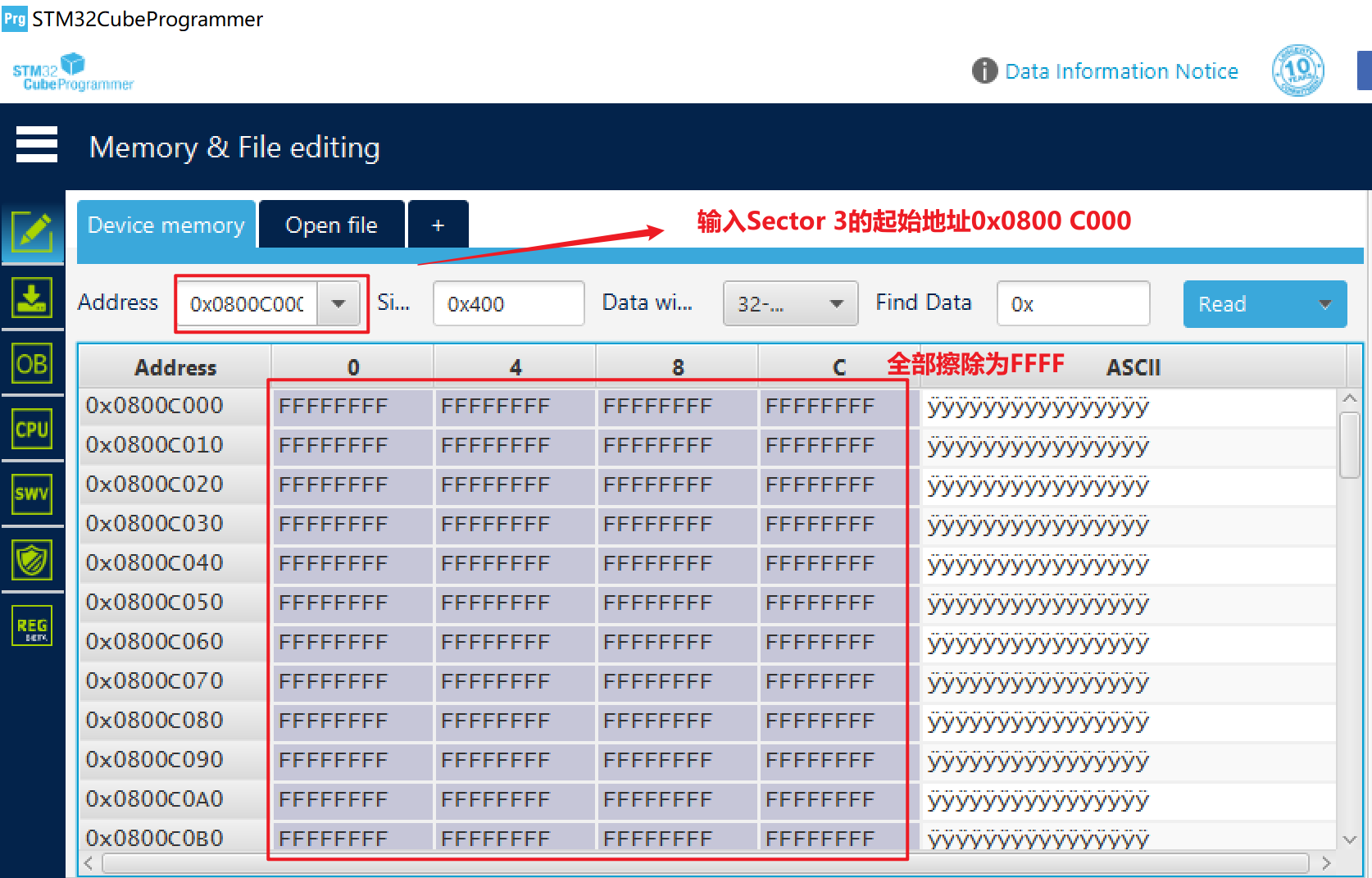
STM32 BootLoader 刷新项目 (十) Flash擦除-命令0x56
STM32 BootLoader 刷新项目 (十) Flash擦除-命令0x56 1. STM32F407 BootLoader 中的 Flash 擦除功能详解 在嵌入式系统中,BootLoader 的设计是非常关键的部分,它负责引导主程序的启动、升级以及安全管理。而在 STM32F407 等 MCU 上实现 BootLoader&…...

POI word转pdf乱码问题处理
1.使用poi 转换word文档成pdf 导入依赖 <dependency><groupId>com.aspose</groupId><artifactId>words</artifactId><version>16.8.0</version></dependency>2.代码实现: SneakyThrowspublic void wordToPdf(String docPath,…...

【GeekBand】C++设计模式笔记11_Builder_构建器
1. “对象创建” 模式 通过 “对象创建” 模式绕开new,来避免对象创建(new)过程中所导致的紧耦合(依赖具体类),从而支持对象创建的稳定。它是接口抽象之后的第一步工作。典型模式 Factory MethodAbstract …...

面试经典 150 题:20、2、228、122
20. 有效的括号 参考代码 #include <stack>class Solution { public:bool isValid(string s) {if(s.size() < 2){ //特判:空字符串和一个字符的情况return false;}bool flag true;stack<char> st; //栈for(int i0; i<s.size(); i){if(s[i] ( |…...

SQL面试题——持续增长问题
持续增长我们也可以称之为连续增长,本质上还是连续类的问题,前面我们已经介绍过 SQL面试题——最大连续登陆问题 SQL面试题——球员连续四次得分 SQL面试题——间隔连续问题 SQL面试题——蚂蚁SQL面试题 连续3天减少碳排放量不低于100的用户 你可以看看之前的文章,了解…...

nginx源码安装配置ssl域名
nginx源码安装 下载 wget http://nginx.org/download/nginx-1.24.0.tar.gz 解压 tar -zxvf nginx-1.24.0.tar.gz 下载openssl apt install openssl 安装nginx cd nginx-1.24.0 sudo apt-get install libpcre3 libpcre3-dev ./configure --prefix=/home/nginx24 --with-http_ss…...

每日一博 - Java的Shallow Copy和Deep Copy
文章目录 概述创建对象的5种方式1. 通过new关键字2. 通过Class类的newInstance()方法3. 通过Constructor类的newInstance方法4. 利用Clone方法5. 反序列化 Clone方法基本类型和引用类型浅拷贝深拷贝如何实现深拷贝1. 让每个引用类型属性内部都重写clone()方法2. 利用序列化 概述…...

.netcore + postgis 保存地图围栏数据
一、数据库字段 字段类型选择(Type) 设置对象类型为:geometry 二、前端传递的Json格式转换 前端传递围栏的各个坐标点数据如下: {"AreaRange": [{"lat": 30.123456,"lng": 120.123456},{"lat": 30.123456…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
