用mv命令替换rm命令
# 用mv命令替换rm命令
主要内容来源自以上博文
rm命令穷凶极恶,以下为替换命令的方式,必做
步骤
- 修改
vim ~/.bashrc - 加入以下代码
mkdir -p ~/.trash #在家目录下创建一个.trash文件夹(隐藏文件,ls -a 查看)
alias rm=del #使用别名del代替rm
del() #函数del,作用:将rm命令修改为mv命令
{ mv $@ ~/.trash/
}
- 保存退出
- 输入
source ~/.bashrc使生效
测试
之前已经打开的窗口仍然使用是默认的rm命令,需要关闭
需要新开两个终端测试,不然有时显示无效,很难看出效果
- 删除文件
del [文件名]
rm [文件名] #换成mv命令,因此不需要加rf参数
del *
rm *
2、清空回收站(即:清空.trash文件夹)
注:rm命令已经删除,所以要彻底删除文件的话,使用 /bin/rm -rf ~/.trash/* 彻底清除垃圾箱里的所有文件。
后面可以安心删除rm了
相关文章:

用mv命令替换rm命令
# 用mv命令替换rm命令 主要内容来源自以上博文 rm命令穷凶极恶,以下为替换命令的方式,必做 步骤 修改vim ~/.bashrc加入以下代码 mkdir -p ~/.trash #在家目录下创建一个.trash文件夹(隐藏文件,ls -a 查看) alias rmdel #使用别名…...

电解车间铜业机器人剥片技术是现代铜冶炼过程中自动化和智能化的重要体现
电解车间铜业机器人剥片技术是现代铜冶炼过程中自动化和智能化的重要体现 电解车间铜业机器人剥片技术是现代铜冶炼过程中自动化和智能化的重要体现,它主要应用于铜电解精炼的最后阶段,即从阴极板上剥离出纯铜的过程。以下是该技术的几个关键点ÿ…...
【qt】控件2
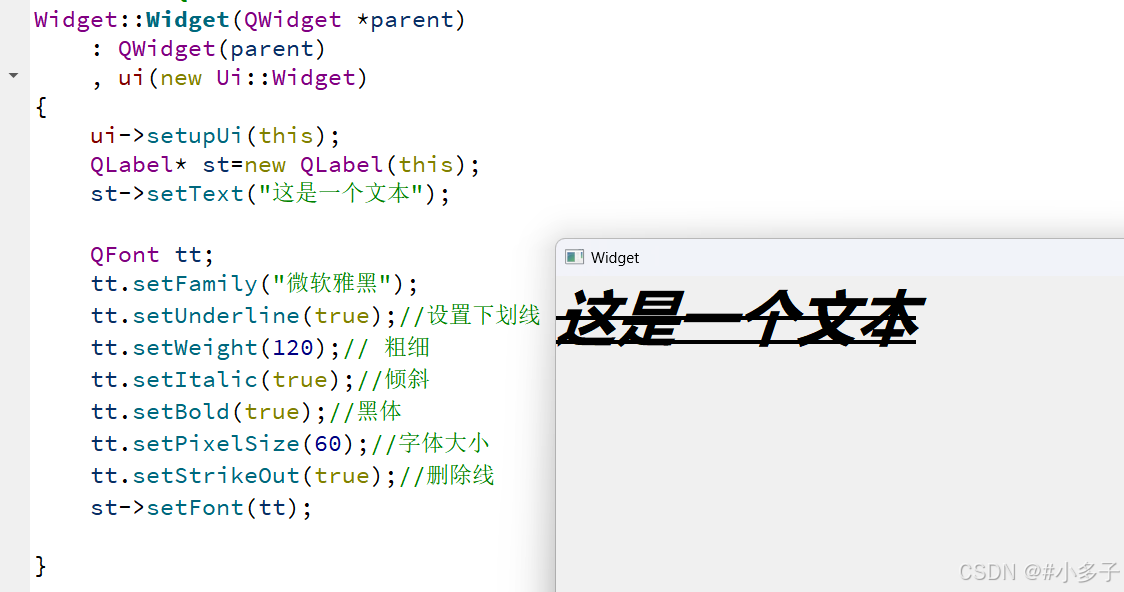
1.frameGeometry和Geometry区别 frameGeometry是开始从红圈开始算,Geometry从黑圈算 程序证明:使用一个按键,当按键按下,qdebug打印各自左上角的坐标(相当于屏幕左上角),以及窗口大小 Widget::Widget(QWid…...

Frida反调试对抗系列(四)百度加固
本文只是交流技术,如有侵权请联系我删除。 知识星球:https://t.zsxq.com/kNlj4 前言: 上一篇文章我们提到 我们使用github开源魔改好的frida server 但是仍然有一些厂商的server不能通过,那么这篇文章针对百度加固 进行快速通…...

Redis 安全
Redis 安全 Redis是一个开源的,高性能的键值存储系统,它通常被用作数据库,缓存和消息代理。由于其高性能和简单的API,Redis在全球范围内被广泛使用。然而,与其他数据库系统一样,Redis的安全性也是至关重要…...
上交大与上海人工智能研究所联合推出医学多语言模型,模型数据代码开源
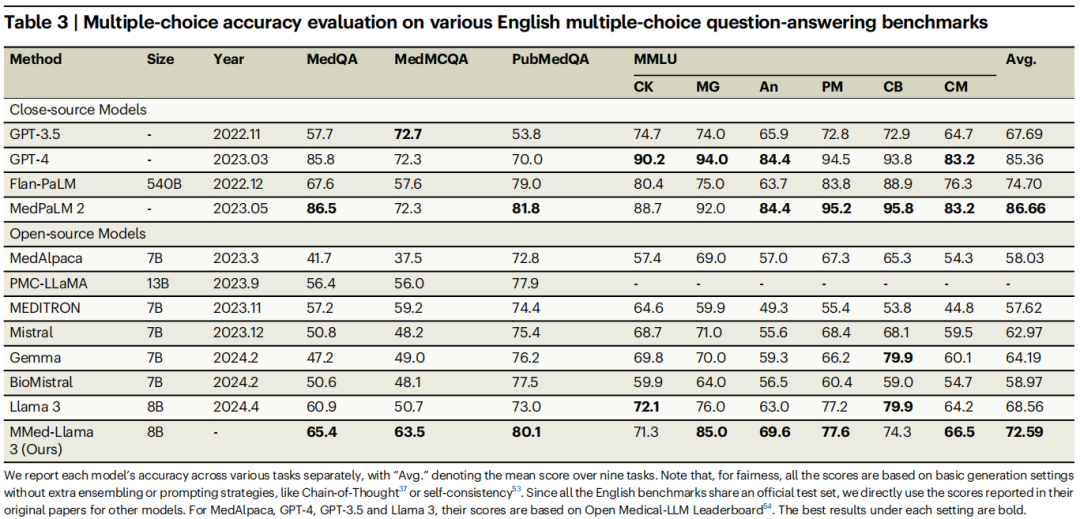
今天为大家介绍的是来自上海交通大学的王延峰与谢伟迪团队的一篇论文。开源的多语言医学语言模型的发展可以惠及来自不同地区、语言多样化的广泛受众。 来源丨 DrugAI、 机器人的脑电波 论文:https://www.nature.com/articles/s41467-024-52417-z MMedC࿱…...

网络安全:我们的安全防线
在数字化时代,网络安全已成为国家安全、经济发展和社会稳定的重要组成部分。网络安全不仅仅是技术问题,更是一个涉及政治、经济、文化、社会等多个层面的综合性问题。从宏观到微观,网络安全的重要性不言而喻。 宏观层面:国家安全与…...

理解 Python 中的 __getitem__ 方法:在自定义类中启用索引和切片操作
理解 Python 中的 __getitem__ 方法:在自定义类中启用索引和切片操作 在Python中,__getitem__是一个特殊方法,属于数据模型方法之一,它使得Python对象能够支持下标访问和切片操作。这个方法提供了一种机制,允许类的实…...

【数据结构】【线性表】【练习】反转链表
申明 该题源自力扣题库19,文章内容(代码,图表等)均原创,侵删! 题目 给你单链表的头指针head以及两个整数left和right,其中left<right,请你反转从位置left到right的链表节点&…...

vue2+3 —— Day5/6
自定义指令 自定义指令 需求:当页面加载时,让元素获取焦点(一进页面,输入框就获取焦点) 常规操作:操作dom “dom元素.focus()” 获取dom元素还要用ref 和 $refs <input ref"inp" type&quo…...

汽车资讯新视角:Spring Boot技术革新
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...

关于win11电脑连接wifi的同时,开启热点供其它设备连接
背景: 我想要捕获手机流量,需要让手机连接上电脑的热点。那么问题来了,我是笔记本电脑,只能连接wifi上网,此时我的笔记本电脑还能开启热点供手机连接吗?可以。 上述内容,涉及到3台设备&#x…...

【Apache Paimon】-- 2 -- 核心特性 (0.9.0)
目录 1、实时更新 1.1、实时大批量更新 1.2、支持定义合并引擎 1.3、支持定义更新日志生成器 2、海量数据追加处理 2.1、append table 2.2、快速查询 3、数据湖功能(类比:hudi、iceberg、delta) 3.1、支持 ACID 事务 3.2、支持 Time…...

golang对日期格式化
1.对日期格式化为 YYYY-mm-dd, 并且没有数据时,返回空 import ("encoding/json""time" )type DateTime time.Timetype SysRole struct {RoleId int64 gorm:"type:bigint(20);primary_key;auto_increment;角色ID;" json:&quo…...
【数据结构与算法】排序
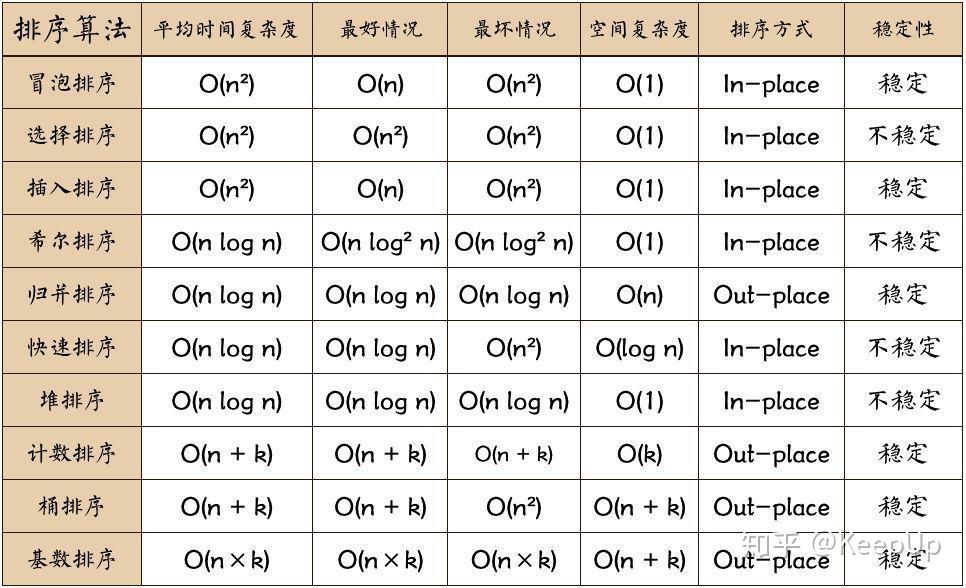
文章目录 排序1.基本概念2.分类2.存储结构 一.插入排序1.1直接插入排序1.2折半插入排序1.3希尔排序 二.选择排序2.1简单选择排序2.2堆排序 三.交换排序3.1冒泡排序3.2快速排序 四.归并排序五.基数排序**总结** 排序 1.基本概念 排序(sorting)又称分类&…...

前端常见的几个包管理工具详解
文章目录 前端常见的几个包管理工具详解一、引言二、包管理工具详解1、npm1.1、npm的安装与使用 2、yarn2.1、yarn的安装与使用 3、pnpm3.1、pnpm的安装与使用 三、步骤二4、包管理工具的选择 四、总结优缺点对比 前端常见的几个包管理工具详解 一、引言 在前端开发的世界里&…...
PyAEDT:Ansys Electronics Desktop API 简介
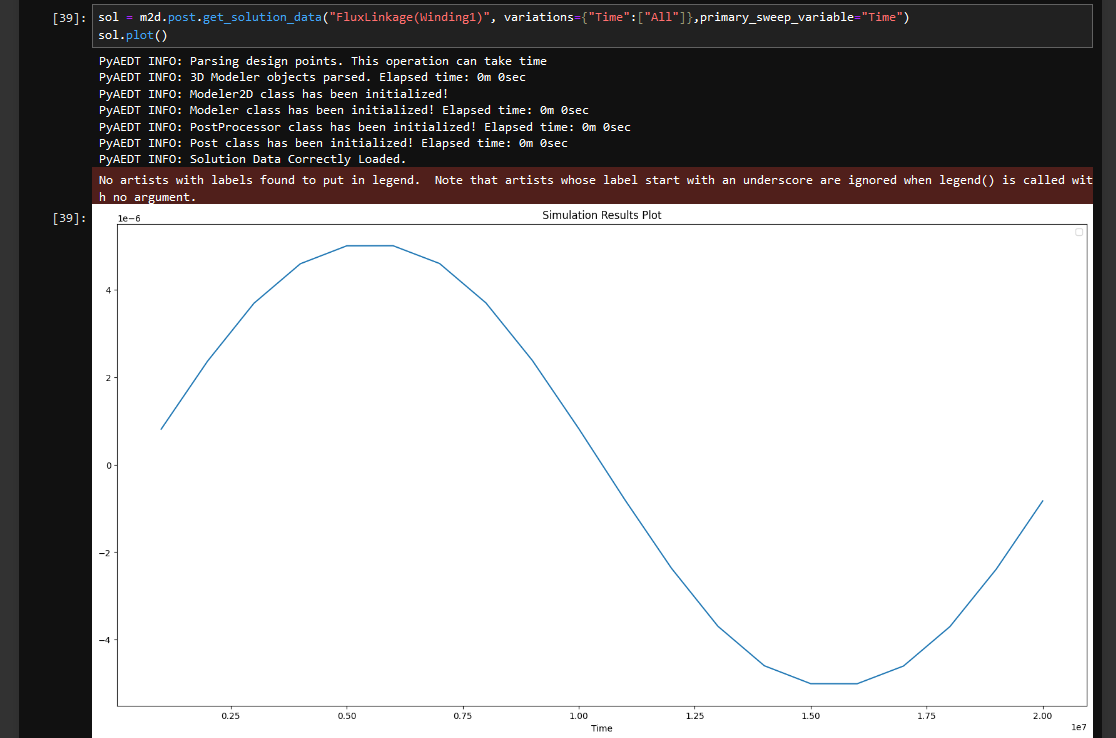
在本文中,我将向您介绍 PyAEDT,这是一个 Python 库,旨在增强您对 Ansys Electronics Desktop 或 AEDT 的体验。PyAEDT 通过直接与 AEDT API 交互来简化脚本编写,从而允许在 Ansys 的电磁、热和机械求解器套件之间无缝集成。通过利…...
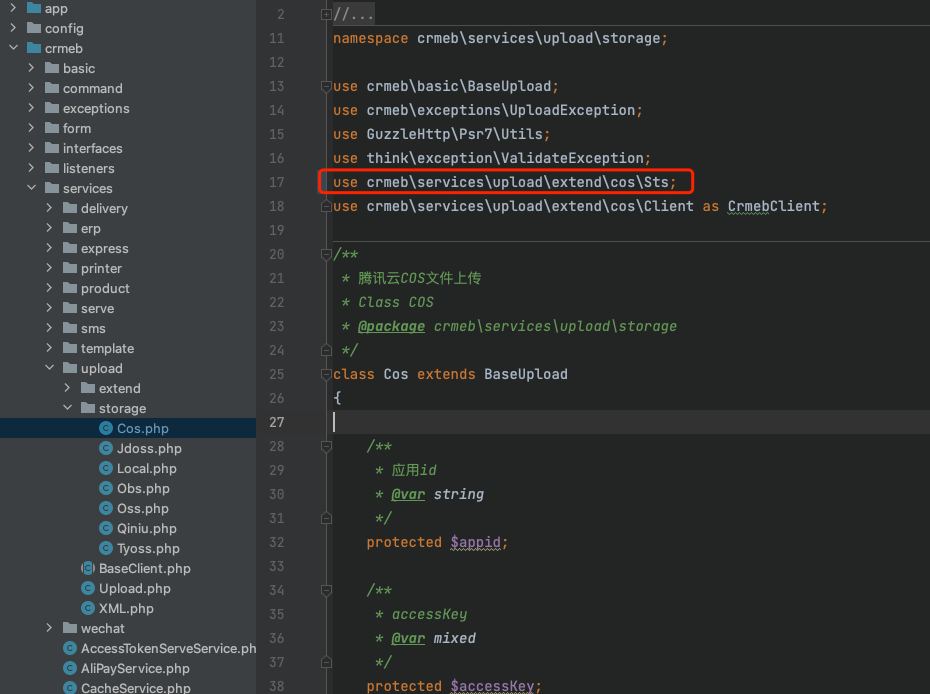
腾讯云存储COS上传视频报错
bug表现为:通过COS上传视频时报错"Class \"QCloud\\COSSTS\\Sts\" not found" 修复办法为:找到文件crmeb/services/upload/storage/Cos.php 将Sts引入由QCloud\COSSTS\Sts;改为crmeb\services\upload\extend\cos\Sts; 修改后重启服…...
 如何在Tomcat中配置访问日志?)
Tomcat(17) 如何在Tomcat中配置访问日志?
在Apache Tomcat中配置访问日志是一个重要的步骤,它可以帮助你跟踪和分析服务器的HTTP请求。访问日志通常记录了每个请求的详细信息,如客户端IP地址、请求时间、请求的URL、HTTP状态码等。以下是如何在Tomcat中配置访问日志的详细步骤和代码示例。 步骤…...

根据频繁标记frequent_token,累加size
根据频繁标记frequent_token,累加size for k, v in contents.items(): 0 (LDAP Built with OpenLDAP LDAP / SDK, /:=@) 1 (LDAP SSL support unavailable, :) 2 (suEXEC mechanism enabled lili wrapper /usr/sbin/suexec, ()/:) 3 (Digest generating secret for digest au…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
