北航软件算法C4--图部分
C4上级图部分
- TOPO!
- 步骤
- 代码段
- TOPO排序部分
- 完整代码
- 简单的图图
- 题目描述
- 输入输出
- 样例
- 步骤
- 代码段
- 开辟vector容器作为dist二维数组
- 初始化
- 调用Floyd算法
- 查询
- 完整代码
- 负环
- 题目描述
- 输入输出
- 样例
- 步骤
- 代码段
- 全局变量定义
- spfa1函数用于判断是否有负环
- spfa2用于记录每个点到1号点的距离
- 完整代码
- 直击西溜线(地铁最短换乘次数)
- 题目描述
- 输入输出
- 样例
- 步骤
- tip
- 代码段
- 全局变量设定
- 完整代码
- Email loss
- 题目描述
- 输入输出
- 样例
- tip
- 步骤
- 代码段
- 全局变量设定
- 完整代码
- 莫卡的最远点对
- 题目描述
- 输入输出
- 样例
TOPO!


步骤
这道题比较简单,因为是要从大到小输出,所以用队列的时候,用上大根堆。(还记得建小堆怎么建吗?)
priority_queue<int,vector< int >,greater< int >> heap;
三个参数都不能少哈↑
构建大根堆只需写 priority_queue< int >
如果没说顺序,那么可以用y总的手搓队列。
代码段
int e[N],ne[N],idx,h[N];
/*
e[i]表示第i个点的值,
ne[i]表示第i个点的next点的下标(编号
h[a]是值为a的点指向的点的下标)
*/
int n,m;
int dgr[N];//dgr[i]表示值为i的点对应的下标
//注意一定是值,不是编号,
int toposort[N];//存放排序结果
int INDEX;
TOPO排序部分
void topo(){priority_queue<int> heap;//如果没说要按什么顺序输出,那普通的队列就可以for(int i=1;i<=n;i++){if(dgr[i]==0){heap.push(i);//先把所有入度为0的点全部放进去}}while(!heap.empty()){int top = heap.top();heap.pop();toposort[INDEX++]=top;//取堆顶for(int i=h[top];i!=-1;i=ne[i]){//把堆顶点连着的点全部都遍历一遍,所有点的入度都减一,如果他变为0了,那么入堆int val = e[i];dgr[val]--;if(dgr[val]==0){heap.push(val);}}}for(int i=0;i<n;i++){cout<<toposort[i]<<' ';}
}
完整代码
#include <iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e6+3;
int e[N],ne[N],idx,h[N];
int n,m;
int dgr[N];
int toposort[N];//存放排序结果
int INDEX;
void add(int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}void topo(){priority_queue<int> heap;for(int i=1;i<=n;i++){if(dgr[i]==0){heap.push(i);}}while(!heap.empty()){int top = heap.top();heap.pop();toposort[INDEX++]=top;for(int i=h[top];i!=-1;i=ne[i]){int val = e[i];dgr[val]--;if(dgr[val]==0){heap.push(val);}}}for(int i=0;i<n;i++){cout<<toposort[i]<<' ';}
}int main(){cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<m;i++){int a,b;cin>>a>>b;add(a,b);dgr[b]++;}topo();
}
简单的图图
题目描述

输入输出

样例

步骤
求多源最短路径,那就是Floyd算法了。
这道题只需要求u到v的最短路径长度,而不需要输出对应的路径序列,因此我们并不需要再开辟path数组,只需要开辟dist数组即可。
path数组用来存放经过的路径,可以用vector开辟一个存放String的二维数组
vector<vector< string >> strings(rows);//rows代表你想开辟的行数
代码段
开辟vector容器作为dist二维数组
vector<vector<ll>> dist(n+1,vector<ll>(n+1,INF));
后面的参数表示有n+1行,每一行是一个vector容器,每个元素初始化为INF最大值
初始化
for(int i=0;i<m;i++){ll u,v,w;cin>>u>>v>>w;dist[u][v]=min(dist[u][v],w);//因为有重边,则只保留值小的那一个
}
for(int i=1;i<=n;i++){dist[i][i]=0;}//对角线初始化为0
调用Floyd算法
for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(dist[i][k]!=INF&&dist[k][j]!=INF)//注意这里要判断一下dist[i][j] = min(dist[i][j],dist[i][k]+dist[k][j]);}}}
查询
int q;cin>>q;while(q--){ll u,v;cin>>u>>v;if(dist[u][v]==INF){cout<<-1<<endl;}else{cout<<dist[u][v]<<endl;}}
完整代码
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
//const int N = 305;
const long long INF = 1e18;
int main(){ll n,m;cin>>n>>m;vector<vector<ll>> dist(n+1,vector<ll>(n+1,INF));for(int i=0;i<m;i++){ll u,v,w;cin>>u>>v>>w;dist[u][v]=min(dist[u][v],w);//因为有重边,则只保留值小的那一个}for(int i=1;i<=n;i++){dist[i][i]=0;}//对角线初始化为0for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(dist[i][k]!=INF&&dist[k][j]!=INF)dist[i][j] = min(dist[i][j],dist[i][k]+dist[k][j]);}}}int q;cin>>q;while(q--){ll u,v;cin>>u>>v;if(dist[u][v]==INF){cout<<-1<<endl;}else{cout<<dist[u][v]<<endl;}}
}
负环
题目描述

输入输出

样例

步骤
- 先使用SPFA算法判断是否有负环,如果有负环,则输出“boo how”
- 要注意,用SPFA判断图内是否有负环的时候,负环不一定在起点到终点的路径上,因此开始初始化队列的时候,需要把所有的点都放进去。原理是:相当于给原图加上了一个虚拟源点,从该点向其他所有点都连着一条权为0的弧。cnt【x】等于n时,说明从x点到0点有n条边,即有n+1个点,而图内最多有n个点,由抽屉原理,在0-x的通路上,必然有两个相同的点。由于spfa每一次松弛操作,都让x到0距离变小,则必然存在负环
- 判断完负环以后,就可以再用一次spfa算法去计算每一个点到1号点的距离了。由于有负权边的存在,只能用spfa或者bellman——ford算法。
- 由于本题是多组数据输入,因此在每一次输出完数据之后,都要记得把该初始化的全都初始化干净。“打扫干净屋子再请客”。
代码段
全局变量定义
#define INF 1e9
const int N = 1e5;
const int M = 1e5;
ll e[M],ne[M],w[M],h[N],idx;//这几个数组,在编译器允许的范围内能开多大
int st[N];//判断第i个点是否在队里
//st数组设成bool类型也可
ll cnt[N],dist[N];//cnt数组记录第i个点到虚拟源点的最短路径的边数
void add(int a,int b,int c){e[idx]=b;ne[idx]=h[a];w[idx]=c;h[a]=idx++;
}
int n,m;
spfa1函数用于判断是否有负环
bool spfa1(){queue<int> q;for(int i=1;i<=n;i++){q.push(i);st[i]=1;}while(q.size()){auto top = q.front();q.pop();st[top]=0;for(int i=h[top];i!=-1;i=ne[i]){int j = e[i];if(dist[j]>dist[top]+w[i]){dist[j]=dist[top]+w[i];cnt[j]=cnt[top]+1;if(cnt[j]>=n){return true;}if(!st[j]){q.push(j);st[j]=1;}}}}return false;
}
spfa2用于记录每个点到1号点的距离
void sfpa2(){fill(dist,dist+N-1,INF);memset(st,0,sizeof st);dist[1]=0;queue<int> q;q.push(1);st[1]=1;while(q.size()){auto top = q.front();q.pop();st[top]=0;for(int i=h[top];i!=-1;i=ne[i]){int j = e[i];if(dist[j]>dist[top]+w[i]){dist[j]=dist[top]+w[i];if(!st[j]){q.push(j);st[j]=1;}}}}for(int i=1;i<=n;i++){cout<<dist[i]<<" ";}puts("");
}
完整代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
typedef long long ll;
#define INF 1e9
const int N = 1e5;
const int M = 1e5;
ll e[M],ne[M],w[M],h[N],idx;
int st[N];
ll cnt[N],dist[N];
void add(int a,int b,int c){e[idx]=b;ne[idx]=h[a];w[idx]=c;h[a]=idx++;
}
int n,m;
bool spfa1(){queue<int> q;for(int i=1;i<=n;i++){q.push(i);st[i]=1;}while(q.size()){auto top = q.front();q.pop();st[top]=0;for(int i=h[top];i!=-1;i=ne[i]){int j = e[i];if(dist[j]>dist[top]+w[i]){dist[j]=dist[top]+w[i];cnt[j]=cnt[top]+1;if(cnt[j]>=n){return true;}if(!st[j]){q.push(j);st[j]=1;}}}}return false;
}
void sfpa2(){fill(dist,dist+N-1,INF);memset(st,0,sizeof st);dist[1]=0;queue<int> q;q.push(1);st[1]=1;while(q.size()){auto top = q.front();q.pop();st[top]=0;for(int i=h[top];i!=-1;i=ne[i]){int j = e[i];if(dist[j]>dist[top]+w[i]){dist[j]=dist[top]+w[i];if(!st[j]){q.push(j);st[j]=1;}}}}for(int i=1;i<=n;i++){cout<<dist[i]<<" ";}puts("");
}
int main(){int t;cin>>t;while(t--){cin>>n>>m;//该初始化的都一定一定要初始化,不然各组数据之间会串联memset(h,-1,sizeof h);memset(dist,0,sizeof dist);memset(cnt,0,sizeof cnt);memset(st,0,sizeof st);for(int i=0;i<m;i++){ll a,b,c;cin>>a>>b>>c;add(a,b,c);}if(spfa1()){cout<<"boo how"<<endl;continue;}else{sfpa2();}}
}
直击西溜线(地铁最短换乘次数)
题目描述

输入输出

样例

步骤
- 存储每次查询的起点和终点
- 存储每条线路的站点
- 存储每条线路站点的同时,将线路号加到map中每个站点对应的数组中(专门存放这个站点都属于哪些线路)
- 处理G【】【】邻接矩阵,用于表示每两条线路之间的换乘代价。初始化时,如果两条线之间没有直接换乘点,初始化为无穷;同一条线,初始化为0;有直接换乘点,初始化为1
- 用floyd算法计算每两条线路之间的最少换乘次数,更新G邻接矩阵
- 遍历每次查询的起点和终点,取它们所在的所有线路,找到换乘次数最小的两条线。
- 注意,最少换乘次数和最少乘坐站数不一样。最少换乘次数相当于把同一条线上抽象成了一个点,最少乘坐站数则直接用floyd或者dijikstra算法就可解决。
tip
- 输入需要用getline(cin,需要输入的内容) ,cin>>输入不能读取字符串之间的空格,而本题地铁站名含有空格。类似地,cin.get()可以用来接受单个字符,也可以接受带空格的字符串
- 由于getline()读到回车就结束,如果输入整数之后,有回车,那么根本就不能正确获取地铁站名,例如:
> int a;
> string b;
> cin>>a;
> //cin.ignore();
> getline(cin,b);
>
> cout<<a<<endl;
> cout<<b<<endl;
如果不加cin.ignore()的话,geline读到a后面的回车就会直接结束输入的
除非你:
 这么输入。
这么输入。
- 访问vector()中的元素,如果没有提前给vector申请空间,那么不能直接用下标访问(这个一会儿结合具体代码说)
代码段
全局变量设定
const int INF = 1e9;
int G[30][30];//两条线路之间是否能换乘
//同一条线路,为0;不同线路可以直接换乘,为1;不同线路不能换乘,INF
vector<pair<string,string>> inquiries;//存放查询的起终点
map<string,vector<int>> mp;//存放每个站点属于哪些线路
vector<string> lines[30];//存放每条线路都有哪些站
int n,q;//地铁线路条数和询问次数
我们这里开辟inquiries和lines都是没有直接申请空间的,因此后面必须先用 resize(m) 给它申请m个空间,才能通过下标访问0-(m-1)的元素。
也可以直接:vector< string > lines(INF);给它开辟INF个空间。二维vector数组初始化可以看看简单的图图那个题
完整代码
void least_change(){ //将G图初始化为INFfill(G[0],G[0]+30*30,INF);cin>>n>>q;cin.ignore();inquiries.resize(q);for(int i=0;i<q;i++){getline(cin,inquiries[i].first);getline(cin,inquiries[i].second);//读取每次询问的起终点 }for(int i=0;i<n;i++){//读取每一条线路int m;cin>>m;cin.ignore();lines[i].resize(m);for(int j=0;j<m;j++){//读取每一条线路的每一个站getline(cin,lines[i][j]); if(j==m-1&&(lines[i][m-1]==lines[i][0]))continue; mp[lines[i][j]].push_back(i);}}//同一线路上的站点,换乘代价为0for(int i=0;i<n;i++){G[i][i]=0;}//不同线路之间,是否能换乘,要手动判断for(auto station:mp){auto belongs = station.second;int sz = belongs.size();for(int i=0;i<sz;i++){for(int j=0;j<sz;j++){if(i!=j&&belongs[i]!=belongs[j])G[belongs[i]][belongs[j]]=1;}}}//floyd算法找到每两条线路之间的最短换乘次数for(int k=0;k<n;k++){for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(G[i][k]!=INF&&G[k][j]!=INF)G[i][j] = min(G[i][j],G[i][k]+G[k][j]);}}}//处理每次查询for(auto inq:inquiries){auto begin_lines = mp[inq.first];auto end_lines = mp[inq.second];// for(int i=0;i<begin_lines.size();i++){// cout<<begin_lines[i]<<" ";// } // puts("");// for(int i=0;i<end_lines.size();i++){// cout<<end_lines[i]<<" ";// } // puts("");int ret = INF; for(int i=0;i<begin_lines.size();i++){for(int j=0;j<end_lines.size();j++){ret = min(ret,G[begin_lines[i]][end_lines[j]]);}}cout<<ret<<endl;}}
int main(){least_change();
}
要注意,环线必须要进行处理
if(j==m-1&&(lines[i][m-1]==lines[i][0]))continue; mp[lines[i][j]].push_back(i);
如果是环线的话,就别重复加它属于第i条线了,因为:
//不同线路之间,是否能换乘,要手动判断for(auto station:mp){auto belongs = station.second;int sz = belongs.size();for(int i=0;i<sz;i++){for(int j=0;j<sz;j++){if(i!=j&&belongs[i]!=belongs[j])G[belongs[i]][belongs[j]]=1;}}}
i ! = j的时候,belongs【i】有可能等于belongs【j】,如果两条线相同的话,换乘代价应该是0,而不是1,因此不需要重复加
Email loss
这题看着唬人,其实就是个求最短路径,没啥难的
题目描述

输入输出

样例

tip
- 注意这里n和m是一个量级的,因此是稀疏图,要用堆优化版的dijikstra算法,如果m和n^2 是一个量级的,那可以用朴素版。
- 无向图和有向图没区别,无向图就是A-B,B-A就行了。
- 其次,dijikstra算法中不能顺便把不能达到的点算了,因为根本就遍历不到它,只能找到s源点可以到达,但是时间超过t的。因此,需要在全部点的最短距离计算结束之后,再统一找不符合的点.
- 如果输出类型是固定的,那么printf要比cout的输出效率更高
- endl还有刷新缓存区的功能,因此多次循环输出如果都用endl的话可能会超时,用"\n"换行效率更高
步骤
先用堆优化dijistra计算所有点到s源点的距离,注意,堆中存储的数据pair<元素1,元素2>,元素1必须是距离,元素2才是编号。因为堆排序的时候默认按照first排序。每次弹出当前回合距离s源点最近的。
代码段
全局变量设定
都是一些套路了
typedef long long ll;
const ll INF = 2e18;
using namespace std;
const int N =1e6+10;
typedef pair<ll,ll> PII;
ll e[N],ne[N],w[N],h[N],idx;
ll n,m,s,t;//点,边,源点,最大时间
ll dist[N];
bool st[N];
完整代码
void solve(){cin>>n>>m>>s>>t;memset(h,-1,sizeof h);fill(dist,dist+N,INF);dist[s]=0;for(ll i=0;i<m;i++){ll a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}priority_queue<PII,vector<PII>,greater<PII>> q;q.push({0,s});//堆优化while(q.size()){auto top = q.top();q.pop();ll val = top.second,distance = top.first;if(st[val])continue;st[val]=true;for(int i=h[val];i!=-1;i=ne[i]){int j = e[i];if(dist[j]>distance+w[i]){dist[j]=distance+w[i];q.push({dist[j],j});}}}vector<PII> vec;for(int i=1;i<=n;i++){if(dist[i]==INF){vec.push_back({i,-1});}else if(dist[i]>t){vec.push_back({i,dist[i]});}}cout<<vec.size()<<"\n";for(auto v :vec){cout<<v.first<<" "<<v.second<<endl;}
}
int main(){solve();return 0;
}
莫卡的最远点对
题目描述

输入输出

样例
 这个题还需要补充一些树型DP还有树的直径的相关知识,等我学了再来写这个题吧
这个题还需要补充一些树型DP还有树的直径的相关知识,等我学了再来写这个题吧
相关文章:

北航软件算法C4--图部分
C4上级图部分 TOPO!步骤代码段TOPO排序部分 完整代码 简单的图图题目描述输入输出样例步骤代码段开辟vector容器作为dist二维数组初始化调用Floyd算法查询 完整代码 负环题目描述输入输出样例步骤代码段全局变量定义spfa1函数用于判断是否有负环spfa2用于记录每个点到1号点的距…...

PCL点云开发-解决在Qt中嵌入点云窗口出现的一闪而过的黑窗口
PCL点云开发-解决在Qt中嵌入点云窗口出现的一闪而过的黑窗口 众所周知,在windows下开发PCL点云最快的方式就是到官网下载其预编译好的库,比如: PCL-1.14.0-AllInOne-msvc2022-win64.exe 这时候你到网络上搜索,大概率会有两种方案…...

本地音乐服务器(二)
4. 上传音乐模块设计 4.1 上传音乐的接口设计 请求和响应设计: 新建music实体类: Data public class Music {private int id;private String title;private String singer;private String time;private String url;private int userid; } 4.2 创建Mu…...

第三十六篇——伯努利试验:到底如何理解随机性?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 概率论指导着我们对于直觉不靠谱的事情,以及为我们如何更高效…...

【Android、IOS、Flutter、鸿蒙、ReactNative 】屏幕适配
Android Java 屏幕适配 参考 今日头条适配依赖配置 添加设计屏幕尺寸 设置字体大小 通过切换不同屏幕尺寸查看字体大小 设置文本宽高 通过切换不同屏幕尺寸查看文本宽高 Android Compose 屏幕适配 <...
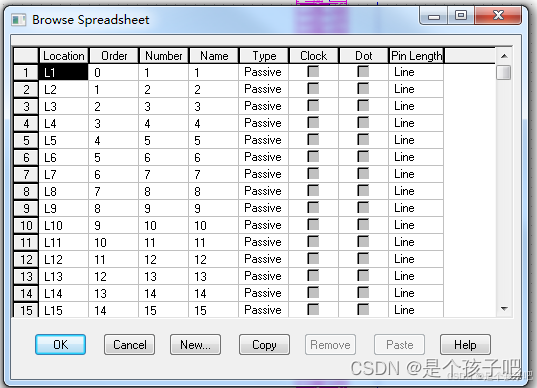
candence : 如何利用EXCEL 绘制复杂、多管脚元件
如何利用EXCEL 绘制复杂、多管脚元件 前面的步骤直接略过 我们以STM32F407VEXX 系列 100pin 芯片为例讲解: 1、新建好一个空元件 2、使用阵列,放置管脚 点击 “ ok ” 3、选中所有管脚 右键 “edit properites” 出现如下页面 4、点击 左上角&…...
)
项目配置文件选择(Json,xml,Yaml, INI)
选择使用哪种类型的配置文件(如 JSON、XML 或其他格式)取决于多个因素,包括项目的需求、团队的熟悉程度、数据结构的复杂性以及可读性和可维护性等。以下是对常见配置文件格式的比较,以及在不同情况下的推荐: 1. JSON&…...

Android 使用Retrofit 以纯二进制文件流上传文件
一、背景 一般上传文件都是以表单形式上传文件,最近项目中涉及到非表单形式上传文件流,分为单个文件流上传、大文件分段上传,此种情景资料较少,这里记录下。 二、方案介绍 2.1 需求协议 1. 上传文件 API 端点:/serv…...

Vue3踩坑记录
目录 一、定义常变量 1.1、ref和reactive到底用谁? 二、双向绑定 2.1、直接改变表格该行数据 2.1、在弹窗改变表格该行数据 一、定义常变量 1.1、ref和reactive到底用谁? 已知:使用ref定义基础类型数据;使用reactive定义复…...

大数据-227 离线数仓 - Flume 自定义拦截器(续接上节) 采集启动日志和事件日志
点一下关注吧!!!非常感谢!!持续更新!!! Java篇开始了! 目前开始更新 MyBatis,一起深入浅出! 目前已经更新到了: Hadoop࿰…...

【热门主题】000054 ECMAScript:现代 Web 开发的核心语言
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 【热…...
【Pytorch】torch.nn.functional模块中的非线性激活函数
在使用torch.nn.functional模块时,需要导入包: from torch.nn import functional 以下是常见激活函数的介绍以及对应的代码示例: tanh (双曲正切) 输出范围:(-1, 1) 特点:中心对称,适合处理归一化后的数据…...

reactflow 中 useNodesState 模块作用
1. 节点状态管理核心功能 useNodesState是一个关键的钩子函数,用于专门管理节点(Nodes)的状态。节点是流程图的核心元素,它们可以代表各种实体,如流程中的任务、系统中的组件或者数据结构中的元素。 useNodesState提…...

Go语言内存分配源码分析学习笔记
大家好,我是V 哥。GO GO GO,今天来说一说Go语言内存分配问题,Go语言内存分配的源码主要集中在runtime包中,它实现了Go语言的内存管理,包括初始化、分配、回收和释放等。下面来对这些过程详细分析一下,先赞后…...

【jvm】方法区常用参数有哪些
目录 1. -XX:PermSize2. -XX:MaxPermSize3. -XX:MetaspaceSize(Java 8及以后)4. -XX:MaxMetaspaceSize(Java 8及以后)5. -Xnoclassgc6. -XX:TraceClassLoading7.-XX:TraceClassUnLoading 1. -XX:PermSize 1.设置JVM初始分配的永久…...

JAVA环境的配置
首先找到JDK环境的官网。 Java Archive Downloads - Java SE 8u211 and laterhttps://www.oracle.com/java/technologies/javase/javase8u211-later-archive-downloads.html 我下载的最后一个x64.exe,下载后,直接双击运行,我这里默认安装到…...

LLM文档对话 —— pdf解析关键问题
一、为什么需要进行pdf解析? 最近在探索ChatPDF和ChatDoc等方案的思路,也就是用LLM实现文档助手。在此记录一些难题和解决方案,首先讲解主要思想,其次以问题回答的形式展开。 二、为什么需要对pdf进行解析? 当利用L…...

MySQL单表查询时索引使用情况
本文针对 MySQL 单表查询时索引使用的几种场景情况进行分析。 假设有一个表如下: CREATE TABLE single_table (id INT NOT NULL AUTO_INCREMENT,key1 VARCHAR(100),key2 INT,key3 VARCHAR(100),key_part1 VARCHAR(100),key_part2 VARCHAR(100),key_part3 VARCHAR(1…...

Qt邮箱程序改良版(信号和槽)
上一版代码可以正常使用,但是会报错 上一篇文章 错误信息 "QSocketNotifier: Socket notifiers cannot be enabled or disabled from another thread" 指出了一个问题,即在非主线程中尝试启用或禁用套接字通知器(QSocketNotifier)…...

入门到精通mysql数据(四)
5、运维篇 5.1、日志 5.1.1、错误日志 错误日志是MySQL中最重要的日志之一,它记录了当mysqld启动和停止,以及服务器在运行过程中发生任何严重错误时的相关信息。当数据库出现任何故障导致无法正常使用时,建议首先查看此日志。 该日志是默认开启的,默认存放目录/var/log…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
