对数几率回归
对数几率回归简介
对数几率回归(Logistic Regression)是一种用于解决分类问题的经典统计模型,其核心思想是利用逻辑函数(Sigmoid函数)将线性回归模型的输出值映射到概率范围 [0, 1],从而实现分类预测。对数几率回归特别适合用于二分类问题。
模型表达式
对数几率回归的概率预测公式为:
其中:
- w为权重向量,x 为输入特征向量,b为偏置项
是 Sigmoid 函数
目标是通过训练确定参数 w 和 b,以最大化模型对数据的预测能力。
极大似然函数与交叉熵损失
极大似然函数
在训练过程中,假设数据集包含 n 个样本,目标是最大化样本标签 y 的条件概率的乘积,即似然函数:
为简化计算,通常对似然函数取对数,得到对数似然函数:
交叉熵损失
对数似然函数的负值称为交叉熵损失,是对数几率回归优化的目标函数:
通过最小化交叉熵损失函数,可以训练出最优的模型参数。
在信息论中涉及信息熵与交叉熵的概念。信息熵越大,表示随机变量的不确定性越大。相对熵=信息熵+交叉熵,相对熵用来度量两个随机变量之间的差异。
参数优化方法
梯度下降法
使用梯度下降法(Gradient Descent)通过迭代更新参数 w 和 b 来最小化损失函数。更新公式为:
其中 η为学习率。
牛顿法
牛顿法是一种二阶优化方法,利用梯度和二阶导数(Hessian 矩阵)更新参数,相较于梯度下降法收敛更快。更新公式为:
其中:
- ∇ℓ 是损失函数的梯度
- H 是 Hessian 矩阵,定义为损失函数的二阶导数矩阵
优点: 牛顿法可以显著加快优化速度,特别是在凸优化问题中表现出色。
缺点: 计算 Hessian 矩阵和求逆的开销较大,不适合大规模数据。
相关文章:
对数几率回归
对数几率回归简介 对数几率回归(Logistic Regression)是一种用于解决分类问题的经典统计模型,其核心思想是利用逻辑函数(Sigmoid函数)将线性回归模型的输出值映射到概率范围 [0, 1],从而实现分类预测。对数…...

docker 配置同宿主机共同网段的IP 同时通过通网段的另一个电脑实现远程连接docker
docker配置网络 #宿主机执行命令 ifconfig 查询对应的主机ip 子网掩码 网关地址 #[网卡名称]:inet[主机IP] netmask[子网掩码] broadcast[网关地址]这里需要重点关注:eno1[网卡名称]以及【192.168.31.225】网关地址 在宿主机执行docker命令创建一个虚拟…...
)
4-7-1.C# 数据容器 - LinkedList(LinkedList 的定义、LinkedList 结点的遍历、LinkedList 的常用方法)
LinkedList 概述 LinkedList<T> 通过节点(Node)来存储数据,每个节点包含数据和指向下一个节点的引用 LinkedList<T> 存储的元素是可重复的 LinkedList<T> 支持泛型,可以指定存储的元素的类型 LinkedList<…...

「三」体验HarmonyOS端云一体化开发模板——使用DevEco Studio直接创建端云一体化工程
关于作者 白晓明 宁夏图尔科技有限公司董事长兼CEO、坚果派联合创始人 华为HDE、润和软件HiHope社区专家、鸿蒙KOL、仓颉KOL 华为开发者学堂/51CTO学堂/CSDN学堂认证讲师 开放原子开源基金会2023开源贡献之星 「目录」 「一」HarmonyOS端云一体化概要 「二」体验HarmonyOS端云一…...

确保以管理员权限运行 Visual Studio 开发者命令提示符
文章目录 解决方法:1. 以管理员身份运行命令提示符2. 改变目录权限3. 改变项目目录位置4. 检查文件系统权限 总结: ********************************************************************** ** Visual Studio 2022 Developer Command Prompt v17.12.0 …...

命令执行简单(棱角社区有毒)
前言:小迪安全2022第一节反弹shell,小迪用的是两台都是云服务器,没有服务器可以在自己的主机上搭建也是可以的,主机上搭两个网站 思路:生成一个木马文件,下载到本机,然后利用本机上传到目标主机…...

Keil基于ARM Compiler 5的工程迁移为ARM Compiler 6的工程
环境: keil版本为5.38,版本务必高于5.30 STM32F4的pack包版本要高于2.9 软件包下载地址:https://zhuanlan.zhihu.com/p/262507061 一、更改Keil中编译器 更改后编译,会报很多错,先不管。 二、更改头文件依赖 观察…...

Kafka-创建topic源码
一、命令创建topic kafka-topics --create --topic quickstart-events --bootstrap-server cdh1:9092 --partitions 2 --replication-factor 2 二、kafka-topics脚本 exec $(dirname $0)/kafka-run-class.sh org.apache.kafka.tools.TopicCommand "$" 脚本中指定了…...
【网络安全】(一) 0成本添加访问级监控
互联网的安全感这个概念源于阿里。顾名思义,让互联网的用户对于web产品能够产生足够的信任和依赖。特别是涉及到用户资金交易的站点,一次严重的用户资料泄露就可以彻底毁掉你的品牌。 然而当前阶段除了bat大部分互联网行业的企业对于网络安全给的重视都…...

【Three.js基础学习】26. Animated galaxy
前言 shaders实现星系 课程回顾 使用顶点着色器为每个粒子设置动画 a属性 , u制服 ,v变化 像素比:window.devicePixelRatio 自动从渲染器检索像素比 renderer.getPixelRatio() 如何尺寸衰减, 放大缩小视角时,粒子都是同…...

vscode使用ssh配置docker容器环境
1 创建容器,并映射主机和容器的指定ssh服务端口 2 进入容器 docker exec -it <容器ID> /bin/bash 3在容器中安装ssh服务 apt-get update apt-get install openssh-server 接着修改ssh文件信息,将容器的10008端口暴露出来允许root用户使用ssh登录 vim /…...
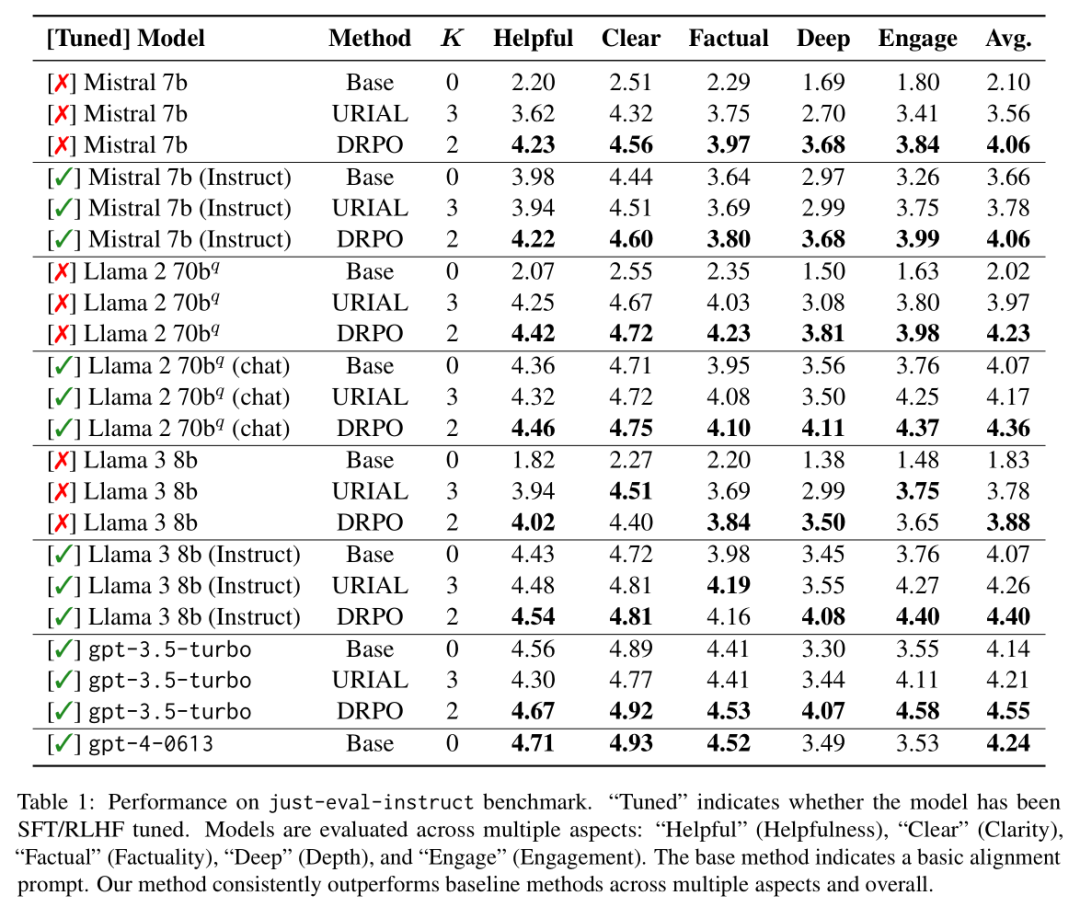
NLP论文速读(EMNLP 2024)|动态奖励与提示优化来帮助语言模型的进行自我对齐
论文速读|Dynamic Rewarding with Prompt Optimization Enables Tuning-free Self-Alignment of Language Models 论文信息: 简介: 本文讨论的背景是大型语言模型(LLMs)的自我对齐问题。传统的LLMs对齐方法依赖于昂贵的训练和人类偏好注释&am…...

【LeetCode】167. 两数之和 II - 输入有序数组
描述 给定一个下标从 1 开始的整数数组numbers,该数组已按非递减顺序排列,请从数组中找出满足相加之和等于目标数target的两个数。如果这两个数分别是numbers[index1]和numbers[index2],返回整数数组[index1, index2]。 只存在唯一答案&#…...
)
Getx:GetxController依赖管理02,Binding绑定全局控制器(懒加载Controller)
在使用GetX 状态管理器的时候,如果每个页面都手动实例化一个控制器就太麻烦了, Binding 的作用就是所有需要进行状态管理的控制器进行统一初始化 创建全局控制器Binding import package:get/get.dart; import ../controllers/counter.dart; // 同上一篇内…...

leetcode 找不同
389. 找不同 已解答 简单 相关标签 相关企业 给定两个字符串 s 和 t ,它们只包含小写字母。 字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。 请找出在 t 中被添加的字母。 示例 1: 输入:s "abcd"…...

2025 - 生信信息学 - GEO数据分析 - RF分析(随机森林)
GEO数据分析 - RF分析(随机森林) 01 准备数据文件 #install.packages("randomForest")#引用包 library(randomForest) set.seed(123456)inputFile"diffGeneExp.txt" #输入文件 setwd("/Users/wangyang/Desktop/BCBM/02ra…...

Matlab深度学习(四)——AlexNet卷积神经网络
网络搭建参考:手撕 CNN 经典网络之 AlexNet(理论篇)-CSDN博客 在实际工程应用中,构建并训练一个大规模的卷积神经网络是比较复杂的,需要大量的数据以及高性能的硬件。如果通过训练好的典型网络稍加改进…...

etcd defrag
场景 prometheus监控告警,告警信息如下 etcd cluster "kube-etcd": database size in use on instance xx is 33.45% of the actual allocated disk space, please run defragmentation (e.g. etcdctl defrag) to retrieve the unused fragmented disk space.处理…...

golang语言整合jwt+gin框架实现token
1.下载jwt go get -u github.com/dgrijalva/jwt-go2.新建生成token和解析token文件 2.1 新建common文件夹和jwtConfig文件夹 新建jwtconfig.go文件 2.2 jwtconfig.go文件代码 /* Time : 2021/8/2 下午3:03 Author : mrxuexi File : main Software: GoLand */ package jwtC…...

数据治理、数据素养和数据质量管理:文献综述
注意:这并不是正式发表的论文,只是一篇用来交作业的文章 摘要 随着数据时代的到来,数据治理、数据素养和数据质量管理成为组织数据管理中的三大核心概念。本文基于相关研究与实践,对这三个领域进行全面综述,探讨它…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
