【视觉SLAM】4b-特征点法估计相机运动之PnP 3D-2D
文章目录
- 0. 前言
- 1. PnP求解
- 1.1 直接线性变换DLT
- 1.2 P3P
- 1.3 光束平差法BA
- 2. 实现
0. 前言
透视n点(Perspective-n-Point,PnP)问题是计算机视觉领域的经典问题,用于求解3D-2D的点运动。换句话说,当知道 N N N个世界坐标系中3D空间点的坐标以及它们在图像上的投影点像素坐标时,可以使用PnP算法来估计相机在世界坐标系的姿态。P3P是最简化的PnP形式,即最少只需3个点即可估计当前的相机姿态(解不唯一)。
总体来说,PnP的求解方法有P3P、直接线性变换(Direct Linear Transformation,DLT)、EPnP(Efficient PnP)和UPnP等。此外,还有非线性优化解法,通过构建最小二乘问题并迭代求解,即万金油式的光束平差法(Bundle Adjustment,BA) 。
1. PnP求解
1.1 直接线性变换DLT
假设有世界坐标系中的3D点 P = [ X , Y , Z , 1 ] T P=[X, Y, Z, 1]^T P=[X,Y,Z,1]T,在图像 I 1 I_1 I1中对应的投影像素点为 x 1 = [ u 1 , v 1 , 1 ] T x_1=[u_1, v_1, 1]^T x1=[u1,v1,1]T,根据相机小孔成像模型有:
s [ u 1 v 1 1 ] = [ R ∣ t ] P = [ t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ] [ X Y Z 1 ] s \begin{bmatrix} u_1 \\ v_1 \\ 1 \end{bmatrix}= \begin{bmatrix} R | t \end{bmatrix} P= \begin{bmatrix} t_1 & t_2 & t_3 & t_4 \\ t_5 & t_6 & t_7 & t_8 \\ t_9 & t_{10} & t_{11} & t_{12} \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} s u1v11 =[R∣t]P= t1t5t9t2t6t10t3t7t11t4t8t12 XYZ1
其中 s = Z s=Z s=Z,利用最后一行将其消去有:
{ s u 1 = t 1 X + t 2 Y + t 3 Z + t 4 s v 1 = t 5 X + t 6 Y + t 7 Z + t 8 s = t 9 X + t 10 Y + t 11 Z + t 12 ⇒ { u 1 = t 1 X + t 2 Y + t 3 Z + t 4 t 9 X + t 10 Y + t 11 Z + t 12 v 1 = t 5 X + t 6 Y + t 7 Z + t 8 t 9 X + t 10 Y + t 11 Z + t 12 \begin{cases} s u_1 = t_1 X + t_2 Y + t_3 Z + t_4\\ s v_1 = t_5 X + t_6 Y + t_7 Z + t_8\\ s = t_9 X + t_{10} Y + t_{11} Z + t_{12} \end{cases} \Rightarrow \begin{cases} u_1 = \frac{t_1 X + t_2 Y + t_3 Z + t_4}{t_9 X + t_{10} Y + t_{11} Z + t_{12}} \\ v_1 = \frac{t_5 X + t_6 Y + t_7 Z + t_8}{t_9 X + t_{10} Y + t_{11} Z + t_{12}} \\ \end{cases} \\ ⎩ ⎨ ⎧su1=t1X+t2Y+t3Z+t4sv1=t5X+t6
相关文章:

【视觉SLAM】4b-特征点法估计相机运动之PnP 3D-2D
文章目录 0. 前言1. PnP求解1.1 直接线性变换DLT1.2 P3P1.3 光束平差法BA2. 实现0. 前言 透视n点(Perspective-n-Point,PnP)问题是计算机视觉领域的经典问题,用于求解3D-2D的点运动。换句话说,当知道 N N N个世界坐标系中3D空间点的坐标以及它们在图像上的投影点像素坐标…...
Asan 内存检测工具)
android 性能分析工具(04)Asan 内存检测工具
1 Asan工具简介 1.1 Asan工具历史背景 AddressSanitizer(ASan)最初由Google开发,并作为LLVM项目的一部分。ASan的设计目的是帮助开发者检测并修复内存错误,如堆栈和全局缓冲区溢出、使用已释放的内存等,这些问题可能…...

html中select标签的选项携带多个值
搜索参考资料:SELECT标签中的选项可以携带多个值吗? 【摘抄】: 它可能有一个select选项中的多个值,如下所示。 <select id"ddlEmployee" class"form-control"> <option value"">-- S…...

Lambda表达式如何进行调试
一、概述 Java8提供了lambda表达式,方便我们对数据集合进行操作,我们使用lambda表达式的时候,是不是有这样的疑问,如何对执行过程中的中间数据进行调试呢? 二、例子 在下面的例子中,我们实现随机最多生成…...

C++ —— 剑斩旧我 破茧成蝶—C++11
江河入海,知识涌动,这是我参与江海计划的第2篇。 目录 1. C11的发展历史 2. 列表初始化 2.1 C98传统的{} 2.2 C11中的{} 2.3 C11中的std::initializer_list 3. 右值引用和移动语义 3.1 左值和右值 3.2 左值引用和右值引用 3.3 引用延长生命周期…...

HTML5好看的音乐播放器多种风格(附源码)
文章目录 1.设计来源1.1 音乐播放器风格1效果1.2 音乐播放器风格2效果1.3 音乐播放器风格3效果1.4 音乐播放器风格4效果1.5 音乐播放器风格5效果 2.效果和源码2.1 动态效果2.2 源代码 源码下载万套模板,程序开发,在线开发,在线沟通 作者&…...

C++设计模式行为模式———迭代器模式中介者模式
文章目录 一、引言二、中介者模式三、总结 一、引言 中介者模式是一种行为设计模式, 能让你减少对象之间混乱无序的依赖关系。 该模式会限制对象之间的直接交互, 迫使它们通过一个中介者对象进行合作。 中介者模式可以减少对象之间混乱无序的依赖关系&…...

FFmpeg 4.3 音视频-多路H265监控录放C++开发十五,解码相关,将h264文件进行帧分隔变成avpacket
前提 前面我们学习了 将YUV数据读取到AVFrame,然后将AVFrame通过 h264编码器变成 AVPacket后,然后将avpacket直接存储到了本地就变成了h264文件。 这一节课,学习解码的一部分。我们需要将 本地存储的h264文件进行帧分隔,也就是变…...

力扣 LeetCode 104. 二叉树的最大深度(Day7:二叉树)
解题思路: 采用后序遍历 首先要区别好什么是高度,什么是深度 最大深度实际上就是根节点的高度 高度的求法是从下往上传,从下往上传实际上就是左右中(后序遍历) 深度的求法是从上往下去寻找 所以采用从下往上 本…...
如何高效实现汤臣倍健营销云数据集成到SQLServer
新版订单同步-(Life-Space)江油泰熙:汤臣倍健营销云数据集成到SQL Server 在企业信息化建设中,数据的高效集成和管理是提升业务运营效率的关键。本文将分享一个实际案例——如何通过新版订单同步方案,将汤臣倍健营销云…...

Vue3中使用:deep修改element-plus的样式无效怎么办?
前言:当我们用 vue3 :deep() 处理 elementui 中 el-dialog_body和el-dislog__header 的时候样式一直无法生效,遇到这种情况怎么办? 解决办法: 1.直接在 dialog 上面增加class 我试过,也不起作用,最后用这种…...

具身智能之Isaac Gym使用
0. 简介 Isaac Gym 是由 NVIDIA 提供的一个高性能仿真平台,专门用于大规模的机器人学习和强化学习(RL)任务。它结合了物理仿真、GPU加速、深度学习框架互操作性等特点,使得研究人员和开发者可以快速进行复杂的机器人仿真和训练。…...

【大数据学习 | Spark】spark-shell开发
spark的代码分为两种 本地代码在driver端直接解析执行没有后续 集群代码,会在driver端进行解析,然后让多个机器进行集群形式的执行计算 spark-shell --master spark://nn1:7077 --executor-cores 2 --executor-memory 2G sc.textFile("/home/ha…...

《Python制作动态爱心粒子特效》
一、实现思路 粒子效果: – 使用Pygame模拟粒子运动,粒子会以爱心的轨迹分布并运动。爱心公式: 爱心的数学公式: x16sin 3 (t),y13cos(t)−5cos(2t)−2cos(3t)−cos(4t) 参数 t t 的范围决定爱心形状。 动态效果: 粒子…...
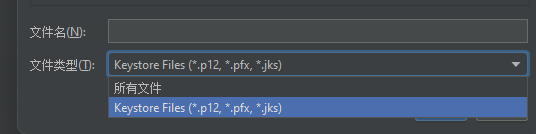
Jmeter 如何导入证书并调用https请求
Jmeter 如何导入证书并调用https请求 通过SSL管理器添加证书文件 支持添加的文件为.p12,.pfx,.jks 如何将pem文件转换为pfx文件? 在公司内部通常会提供3个pem文件。 ca.pem:可以理解为是根证书,用于验证颁发的证…...

Python程序15个提速优化方法
目录 Python程序15个提速优化方法1. 引言2. 方法一:使用内建函数代码示例:解释: 3. 方法二:避免使用全局变量代码示例:解释: 4. 方法三:使用局部变量代码示例:解释: 5. 方…...

足球虚拟越位线技术FIFA OT(二)
足球虚拟越位线技术FIFA OT(二) 在FIFA认证测试过程中,留给VAR系统绘制越位线的时间只有90秒(在比赛中时间可能更短),那么90秒内要做什么事呢,首先场地上球员做出踢球动作,然后VAR要…...

centos7.9单机版安装K8s
1.安装docker [rootlocalhost ~]# hostnamectl set-hostname master [rootlocalhost ~]# bash [rootmaster ~]# mv /etc/yum.repos.d/* /home [rootmaster ~]# curl -o /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo [rootmaster ~]# cu…...

图像编辑一些概念:Image Reconstruction与Image Re-generation
图像编辑本质上是在“图像重建”(image reconstruction)和“图像再生成”(image re-generation)之间寻找平衡。 1. Image Reconstruction(图像重建) 定义:图像重建通常是指从已有的图像中提取信…...

【STM32】在 STM32 USB 设备库添加新的设备类
说实话,我非常想吐槽 STM32 的 USB device library,总感觉很混乱。 USB Device library architecture 根据架构图: Adding a custom class 如果你想添加新的设备类,必须修改的文件有 usbd_desc.cusbd_conf.cusb_device.c 需要…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
