回溯--数据在内存中的存储:整数、大小端和浮点数的深度解析
目录
引言
1. 整数在内存中的存储
1.1 原码、反码和补码
1.2 为什么使用补码?
1.3 示例代码:整数的存储
2. 大小端字节序和字节序判断
2.1 什么是大端和小端?
2.2 为什么会有大端和小端之分?
2.3 字节序的判断小程序
2.4 示例代码:大小端存储的区别
3. 浮点数在内存中的存储
3.1 浮点数的表示方法
3.2 浮点数的存储结构
3.3 浮点数的编码示例
3.4 示例代码:浮点数的存储
3.5 特殊情况:0、无穷和 NaN
4. 内存对齐
4.1 为什么需要内存对齐?
4.2 内存对齐的规则
4.3 示例代码:内存对齐
4.4 使用 #pragma pack 指令
5. 结论
引言
在计算机系统中,数据的存储是非常基础但极其重要的一部分。理解数据在内存中的存储机制不仅有助于我们编写更高效的代码,还可以帮助我们理解一些计算机运行中的底层细节。这篇博客将为大家详细讲解整数和浮点数是如何存储在内存中的,并且会解释大端字节序与小端字节序的区别,最后介绍内存对齐的重要性及其实现方式。
1. 整数在内存中的存储
整数在内存中的存储主要有三种二进制表示方法:原码、反码和补码。在深入理解这三种表示方法之前,我们首先要了解,计算机中的整数是以二进制形式存储的。
1.1 原码、反码和补码
原码:原码是将数值直接按照正负数的形式翻译成二进制。最左边的位(最高位)用于表示符号,0表示正数,1表示负数,其他位用于表示数值。例如,+5 的原码是
00000101,而 -5 的原码则是10000101。反码:反码是对原码的一种变形形式,它的符号位保持不变,其他位按位取反。例如,-5 的反码是
11111010。补码:补码是在反码的基础上加 1 而得到的。例如,-5 的补码是
11111011。在计算机系统中,数据一律用补码来表示和存储,这样做的好处是可以将符号位和数值位统一处理,同时加法和减法也可以统一处理。
1.2 为什么使用补码?
在计算机系统中,使用补码来表示整数有几个显著的优势:
统一处理符号位和数值位:补码的表示方式可以将符号位和数值部分一起进行运算,这简化了计算机的硬件设计。
加法和减法的统一性:在补码的表示方式下,加法和减法可以通过相同的硬件电路实现,CPU 只需要一个加法器。
1.3 示例代码:整数的存储
下面的 C 代码展示了正负整数在内存中的存储方式。
#include <stdio.h>void print_binary(int num)
{for (int i = 31; i >= 0; i--){printf("%d", (num >> i) & 1);if (i % 8 == 0) printf(" ");}printf("\n");
}int main()
{int positive = 5;int negative = -5;printf("正数 5 的补码形式:\n");print_binary(positive);printf("负数 -5 的补码形式:\n");print_binary(negative);return 0;
}运行该代码可以看到 5 和 -5 在内存中的二进制表示,其中负数的补码形式通过对正数按位取反加 1 来得到。
2. 大小端字节序和字节序判断
当数据在内存中存储时,尤其是超过一个字节的数据(如 int 型或 long 型),存储的顺序变得非常重要,这就涉及到 大端字节序(Big-endian) 和 小端字节序(Little-endian) 的概念。
2.1 什么是大端和小端?
大端模式(Big-endian):数据的高位字节内容保存在内存的低地址处,而数据的低位字节内容保存在内存的高地址处。简单来说,就是先存储“大的部分”。
小端模式(Little-endian):数据的低位字节内容保存在内存的低地址处,高位字节内容保存在内存的高地址处,简单来说,就是先存储“小的部分”。
举个例子,假设有一个 16 位的数值 0x1122,在大端模式下,它会被存储为:
地址 0x0010: 0x11
地址 0x0011: 0x22而在小端模式下,则会被存储为:
地址 0x0010: 0x22
地址 0x0011: 0x112.2 为什么会有大端和小端之分?
大小端模式的产生主要与处理器的设计有关。在 X86 结构中,我们普遍采用小端模式,而在一些特殊的嵌入式系统中则使用大端模式。此外,很多 ARM 处理器可以由硬件来选择是大端还是小端模式。
大小端的存在并没有孰优孰劣,更多是与硬件架构的历史和习惯有关。在实际编程中,判断字节序有助于编写跨平台兼容的代码。
2.3 字节序的判断小程序
以下代码可以用来判断当前机器的字节序:
#include <stdio.h>int check_sys()
{int i = 1;return (*(char *)&i);
}int main()
{int ret = check_sys();if(ret == 1){printf("小端字节序\n");}else{printf("大端字节序\n");}return 0;
}在上面的代码中,我们通过将一个整型变量 i 的地址转换为字符指针,并检查其第一个字节的值来判断机器的字节序。如果第一个字节是 1,则说明是小端模式,否则是大端模式。
2.4 示例代码:大小端存储的区别
以下代码展示了大小端存储模式在内存中的差异:
#include <stdio.h>void print_bytes(int num)
{unsigned char *ptr = (unsigned char *)#for (int i = 0; i < sizeof(int); i++){printf("字节 %d: 0x%02x\n", i, ptr[i]);}
}int main()
{int num = 0x11223344;printf("整数 0x11223344 在内存中的存储情况:\n");print_bytes(num);return 0;
}在小端系统上,输出结果为:
字节 0: 0x44
字节 1: 0x33
字节 2: 0x22
字节 3: 0x11而在大端系统上,输出结果则为:
字节 0: 0x11
字节 1: 0x22
字节 2: 0x33
字节 3: 0x443. 浮点数在内存中的存储
浮点数的存储较整数要复杂得多,因为它们需要同时存储符号位、指数和有效数字部分。在计算机中,浮点数通常采用 IEEE 754 标准来表示。
3.1 浮点数的表示方法
根据 IEEE 754 标准,任意一个二进制浮点数 V 可以表示为:
S:符号位,当
S=0时,V为正数;当S=1时,V为负数。M:有效数字,通常是大于等于 1 小于 2 的小数。
E:指数部分。
3.2 浮点数的存储结构
浮点数按照 IEEE 754 标准存储时,32 位的浮点数(即单精度浮点数)和 64 位的浮点数(即双精度浮点数)有不同的结构:
-
32 位浮点数(单精度):
-
符号位 S:1 位
-
指数 E:8 位
-
有效数字 M:23 位
-
-
64 位浮点数(双精度):
-
符号位 S:1 位
-
指数 E:11 位
-
有效数字 M:52 位
-
3.3 浮点数的编码示例
例如,考虑一个十进制数 -5.75,我们想将其编码为 32 位浮点数:
符号位 S:由于数是负数,符号位 S 为
1。转换为二进制:
5.75的二进制形式是101.11。标准化形式:将
101.11写成1.0111 × 2^2。指数 E:指数部分为
2,为了适应偏移量表示,单精度浮点数的偏移量是127,所以E = 2 + 127 = 129,即10000001。有效数字 M:有效数字部分为
0111,后面补0,直到总共占 23 位。
最终,-5.75 的二进制表示为:
1 | 10000001 | 011100000000000000000003.4 示例代码:浮点数的存储
以下代码展示了浮点数在内存中的存储:
#include <stdio.h>void print_float_bits(float num)
{unsigned char *ptr = (unsigned char *)#for (int i = 0; i < sizeof(float); i++){printf("字节 %d: 0x%02x\n", i, ptr[i]);}
}int main()
{float num = 5.75;printf("浮点数 5.75 在内存中的存储情况:\n");print_float_bits(num);return 0;
}运行该代码,可以看到浮点数 5.75 在内存中的表示形式。浮点数的存储涉及到符号位、指数和有效数字的组合,因此其内存表示比整数更复杂。
3.5 特殊情况:0、无穷和 NaN
零的表示:当符号位为
0或1,指数部分和有效数字部分全为0时,表示+0或-0。无穷大和负无穷大:当指数部分全为
1,有效数字部分全为0时,表示正无穷(+∞)或负无穷(-∞)。NaN(Not a Number):当指数部分全为
1,有效数字部分不全为0时,表示 NaN,用于表示未定义的结果(例如0/0或√-1)。
4. 内存对齐
内存对齐是指数据在内存中的存放方式,需要遵循特定的对齐边界规则。内存对齐的目的是为了提高 CPU 访问数据的效率,因为大多数处理器在对齐边界上访问数据时效率更高。
4.1 为什么需要内存对齐?
内存对齐的主要原因有以下几点:
性能:现代 CPU 在读取内存数据时,如果数据地址是对齐的,读取速度会更快。对于非对齐的数据,CPU 可能需要执行多次内存访问,导致性能下降。
硬件限制:某些架构的 CPU 只能从特定的对齐地址读取数据,否则会产生硬件异常。
4.2 内存对齐的规则
内存对齐通常遵循以下规则:
数据类型的对齐边界等于数据类型的大小。例如,
int类型通常是 4 个字节,因此它必须位于 4 的倍数的地址上。结构体的总大小也应该是其最大成员对齐边界的整数倍,这样可以确保结构体数组中的每个元素都能正确对齐。
4.3 示例代码:内存对齐
以下代码展示了结构体在内存中的对齐情况:
#include <stdio.h>struct Example
{char a;int b;short c;
};int main()
{struct Example ex;printf("结构体 Example 的大小: %lu\n", sizeof(ex));return 0;
}在大多数编译器中,结构体 Example 的大小可能是 12 字节,而不是简单的所有成员大小之和(1 + 4 + 2 = 7 字节)。这是因为编译器会插入填充字节来确保每个成员的对齐。
char a后面会有 3 个填充字节,使得int b可以位于 4 字节对齐的地址。
short c也会被对齐到 2 字节的边界上。
4.4 使用 #pragma pack 指令
在一些情况下,我们希望取消编译器的默认对齐方式,可以使用 #pragma pack 指令来更改对齐规则。例如:
#include <stdio.h>#pragma pack(1)
struct PackedExample
{char a;int b;short c;
};
#pragma pack()int main()
{struct PackedExample ex;printf("结构体 PackedExample 的大小: %lu\n", sizeof(ex));return 0;
}使用 #pragma pack(1) 后,结构体的大小将变为 7 字节,因为编译器不再插入填充字节。但是,这样做可能会导致性能下降,因为读取未对齐的数据需要更多的 CPU 周期。
5. 结论
数据在内存中的存储是理解计算机系统的基础之一。
整数的存储涉及到原码、反码和补码的概念,而大小端字节序则影响了多字节数据的存储顺序。
浮点数的存储更为复杂,需要考虑符号位、指数和有效数字的表示。
内存对齐则是为了提高 CPU 访问数据的效率,通过对齐边界来优化内存访问性能。通过对这些内容的深入理解,我们可以更好地编写高效且可靠的程序,并理解程序在底层是如何运行的。
Now,以上便是本期回溯C语言的全部内容啦,希望对大家有所帮助。同时也欢迎大家在评论区与我交流,共同进步!
相关文章:

回溯--数据在内存中的存储:整数、大小端和浮点数的深度解析
目录 引言 1. 整数在内存中的存储 1.1 原码、反码和补码 1.2 为什么使用补码? 1.3 示例代码:整数的存储 2. 大小端字节序和字节序判断 2.1 什么是大端和小端? 2.2 为什么会有大端和小端之分? 2.3 字节序的判断小程序 2.…...

第二十二章 Spring之假如让你来写AOP——Target Object(目标对象)篇
Spring源码阅读目录 第一部分——IOC篇 第一章 Spring之最熟悉的陌生人——IOC 第二章 Spring之假如让你来写IOC容器——加载资源篇 第三章 Spring之假如让你来写IOC容器——解析配置文件篇 第四章 Spring之假如让你来写IOC容器——XML配置文件篇 第五章 Spring之假如让你来写…...

探索设计模式:原型模式
设计模式之原型模式 🧐1. 概念🎯2. 原型模式的作用📦3. 实现1. 定义原型接口2. 定义具体的原型类3. 定义客户端4. 结果 📰 4. 应用场景🔍5. 深拷贝和浅拷贝 在面向对象编程中,设计模式是一种通用的解决方案…...
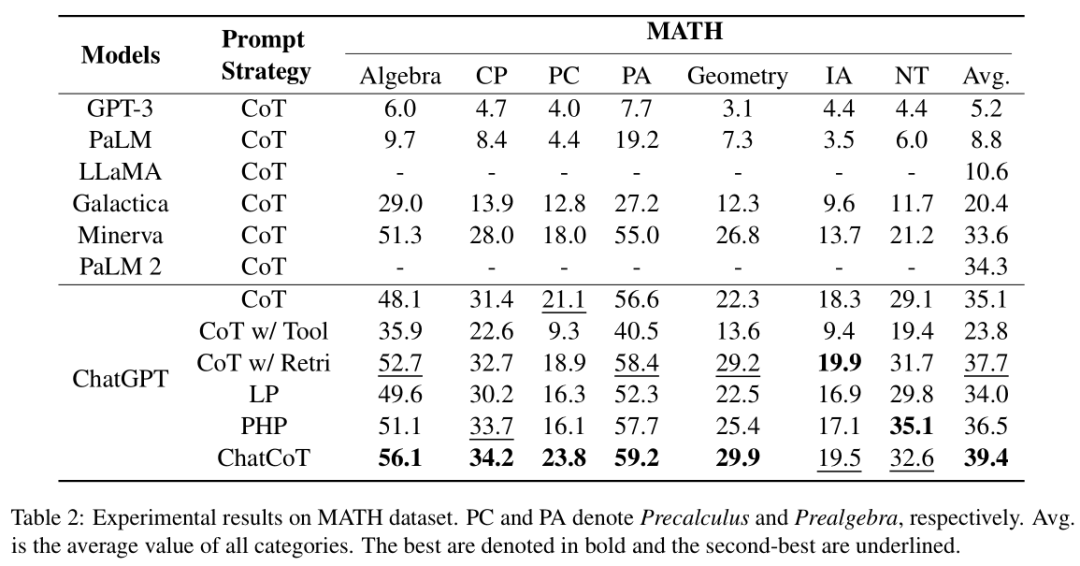
NLP论文速读(EMNLP 2023)|工具增强的思维链推理
论文速读|ChatCoT: Tool-Augmented Chain-of-Thought Reasoning on Chat-based Large Language Models 论文信息: 简介: 本文背景是关于大型语言模型(LLMs)在复杂推理任务中的表现。尽管LLMs在多种评估基准测试中取得了优异的成绩…...

JVM垃圾回收详解.②
空间分配担保 空间分配担保是为了确保在 Minor GC 之前老年代本身还有容纳新生代所有对象的剩余空间。 《深入理解 Java 虚拟机》第三章对于空间分配担保的描述如下: JDK 6 Update 24 之前,在发生 Minor GC 之前,虚拟机必须先检查老年代最大…...

什么是事务,事务有什么特性?
事务的四大特性(ACID) 原子性(Atomicity) 解释:原子性确保事务中的所有操作要么全部完成,要么全部不做。这意味着事务是一个不可分割的工作单元。在数据库中,这通常通过将事务的操作序列作为一个…...

深入解析:如何使用 PyTorch 的 SummaryWriter 进行深度学习训练数据的详细记录与可视化
深入解析:如何使用 PyTorch 的 SummaryWriter 进行深度学习训练数据的详细记录与可视化 为了更全面和详细地解释如何使用 PyTorch 的 SummaryWriter 进行模型训练数据的记录和可视化,我们可以从以下几个方面深入探讨: 初始化 SummaryWriter…...

企业微信中设置回调接口url以及验证 spring boot项目实现
官方文档: 接收消息与事件: 加密解密文档:加解密库下载与返回码 - 文档 - 企业微信开发者中心 下载java样例 加解密库下载与返回码 - 文档 - 企业微信开发者中心 将解压开的代码 ‘将文件夹:qq\weixin\mp\aes的代码作为工具拷…...

电脑超频是什么意思?超频的好处和坏处
嗨,亲爱的小伙伴!你是否曾经听说过电脑超频?在电脑爱好者的圈子里,这个词似乎非常熟悉,但对很多普通用户来说,它可能还是一个神秘而陌生的存在。 今天,我将带你揭开超频的神秘面纱,…...
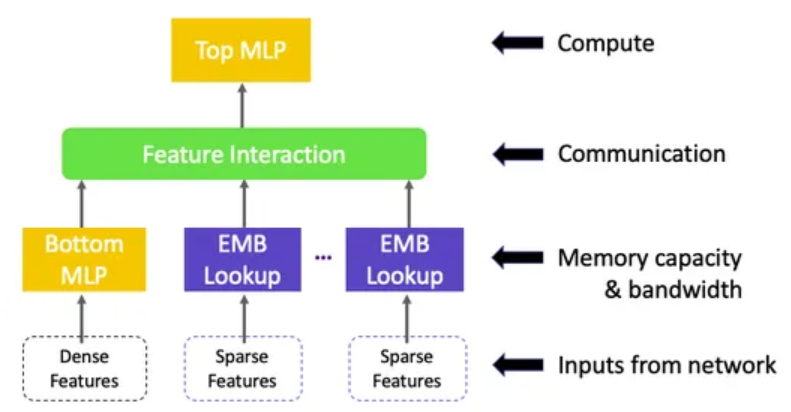
在 AMD GPU 上构建深度学习推荐模型
Deep Learning Recommendation Models on AMD GPUs — ROCm Blogs 2024 年 6 月 28 日 发布者 Phillip Dang 在这篇博客中,我们将演示如何在支持 ROCm 的 AMD GPU 上使用 PyTorch 构建一个简单的深度学习推荐模型 (DLRM)。 简介 DLRM 位于推荐系统和深度学习的交汇…...

阿里云IIS虚拟主机部署ssl证书
宝塔配置SSL证书用起来是很方便的,只需要在站点里就可以配置好,但是云虚拟主机在管理的时候是没有这个权限的,只提供了简单的域名管理等信息。 此处记录下阿里云(原万网)的IIS虚拟主机如何配置部署SSL证书。 进入虚拟…...

Python运算符列表
运算符 描述 xy,x—y 加、减,“"号可重载为连接符 x*y,x**y,x/y,x%y 相乘、求平方、相除、求余,“*”号可重载为重复,“%"号可重载为格式化 <,<,&…...

MFC图形函数学习09——画多边形函数
这里所说的多边形是指在同一平面中由多条边构成的封闭图形,强调封闭二字,否则无法进行颜色填充,多边形包括凸多边形和凹多边形。 一、绘制多边形函数 原型:BOOL Polygon(LPPOINT lpPoints,int nCount); 参数&#x…...

GaussianDreamer: Fast Generation from Text to 3D Gaussians——点云论文阅读(11)
此内容是论文总结,重点看思路!! 文章概述 本文提出了一种快速从文本生成3D资产的新方法,通过结合3D高斯点表示、3D扩散模型和2D扩散模型的优势,实现了高效生成。该方法利用3D扩散模型生成初始几何,通过噪声…...

k8s篇之控制器类型以及各自的适用场景
1. k8s中控制器介绍 在 Kubernetes 中,控制器(Controller)是集群中用于管理资源的关键组件。 它们的核心作用是确保集群中的资源状态符合用户的期望,并在需要时自动进行调整。 Kubernetes 提供了多种不同类型的控制器,每种控制器都有其独特的功能和应用场景。 2. 常见的…...
:express路由)
Node.js 笔记(一):express路由
代码 建立app.js文件,代码如下: const express require(express) const app express() const port 3002app.get(/,(req,res)>{res.send(hello world!)})app.listen(port,()>{console.log(sever is running on http://localhost:${port}) })问…...

bash笔记
0 $0 是脚本的名称,$# 是传入的参数数量,$1 是第一个参数,$BOOK_ID 是变量BOOK_ID的内容 1 -echo用于在命令窗口输出信息 -$():是命令替换的语法。$(...) 会执行括号内的命令,并将其输出捕获为一个字符串ÿ…...

mongoDB副本集搭建-docker
MongoDB副本集搭建-docker 注:在进行副本集搭建前,请先将服务部署docker环境并正常运行。 #通过--platform指定下载镜像的系统架构 在这我用的是mongo:4.0.28版本 arm64系统架构的mongo镜像 docker pull --platformlinux/arm64 mongo:4.0.2#查看镜像是…...

Python软体中使用 Flask 或 FastAPI 搭建简单 RESTful API 服务并实现限流功能
Python软体中使用 Flask 或 FastAPI 搭建简单 RESTful API 服务并实现限流功能 引言 在现代 web 开发中,RESTful API 已成为应用程序之间进行通信的标准方式。Python 提供了多种框架来帮助开发者快速搭建 RESTful API 服务,其中 Flask 和 FastAPI 是最受欢迎的两个框架。本…...

CentOS操作系统下安装Nacos
CentOS下安装Nacos 前言 这在Centos下安装配置Nacos 下载Linux版Nacos 首先到Nacos的 Github页面,找到所需要安装的版本 也可以右键复制到链接,然后通过wget命令进行下载 wget https://github.com/alibaba/nacos/releases/download/1.3.2/nacos-ser…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
