底层逻辑之:极大似然方法(Maximum Likelihood Estimation, MLE)
简介:
极大似然方法(Maximum Likelihood Estimation, MLE)是一种用于估计统计模型参数的方法。其核心思想是基于观测数据来寻找最可能产生这些数据的模型参数。
早在1821年,德国数学家高斯(C. F. Gauss)就利用极大似然方法MLE取估算误差概率分布(正态分布)的概率密度函数。(高斯这老哥的思想领先了100年)
但这一概念则由罗纳德·费希尔(R. A. Fisher)在1922年的论文《On the mathematical foundations of theoretical statistics, reprinted in Contributions to Mathematical Statistics》进行了系统阐述,并且首先探讨了这种方法的一些性质。极大似然估计这一名称也是出自费希尔。
极大似然估计法MLE
描述函数和似然函数
极大似然方法很简单,就是利用观测值去推测数学描述模型的参数。
没错,利用极大似然估计法时,我们需要提前知道观测数值的分布的描述函数(一般为概率密度分布式),或者自己去进行假设结构,只有得到描述函数,将它带入似然函数(Likelihood Function)后,我们才能基于MLE的框架利用偏导求解。
因此,在讲 MLE前,我们要明确两个概念:描述函数和似然函数。这两个概念在MLE中是不同层次的,很多初学者会将两者弄混。
描述函数:描述“发生概率”(或者称为密度)与对象变量x之间的映射关系,这是一个理想化的概率,写为
, 常见的的描述函数如正态分布概率密度函数:
似然函数 :描述描述函数参数变化时,当前抽样结果对应发生概率的函数。写作:
其中,意味,描述函数参数为
组合下,集合X(抽样结果)发生的概率,其值为
(取值0~1),
是单次抽样中,描述函数参数为
组合下,结果为
的概率,这些概率的交集(即连乘)就是最终概率
注意:
根据似然函数的结构特质,抽样的各类事件或数值相互独立,无不影响。
在构建似然函数时,抽样结果是既定发生的(也就是固定的),否者无法进行MLE。
似然函数中,描述函数的可变参数为自变量,抽样结果发生的概率是应变量,因此MLE的本质就是找到一组最佳可变参数,使得既定发生的抽样结果对应发生的概率最大,故称作为最大似然估计。
MLE:基于似然函数对描述函数的参数进行反推
从数学思想的角度来说,MLE就是基于现实得到的数据,基于概率学对描述函数的参数进行反推。
假设神明以80为均值,方差为40以正态分布随机地赋予人类寿命,对于寿命的分布,理想的描述函数为:
对于身为人类的我而言,关于寿命,我什么都不知道,只能借助抽样调查和最大似然估计反向推测神明的设计,于是我做了一项3个单位调查(我们有请MATLAB来帮忙模拟一下):
% 设置均值和方差
mu = 80;
sigma_squared = 40;
sigma = sqrt(sigma_squared); % 标准差是方差的平方根% 随机生成3个样本
num_samples = 3;
samples = normrnd(mu, sigma, [num_samples, 1]);% 显示生成的样本
disp(samples);%%83.400591.598565.7138
人们不能总是直接猜到上帝的想法,在这个问题中,假如我是一个不知道正态分布概率密度函数的白痴,要不这个问题就太简单了,没办法体现MLE的用法
得到抽样数据后,我认为神明关于寿命的安排应该是长这个样吧:一个以e为底的对数函数,满足以x=c点中心对称,且其在定义域的积为1。(当然,以2、3、4其他自数为底也是可以的,但是对数求导过程会复杂一些,有兴趣的读者可以自己去尝试一下)
其中,定义域的积必须为1,否则其参数的偏导=0会无解
即:
令
根据高斯积分定义
且
原式:
故a、d、b应满足:
既然如此,我们就用d和b表示a吧,于是:
d被消掉了 令新b=-b变化一下:
看来不需要上帝,我凭实力构建了一个类正态概率密度函数(笑)
继续!
根据MLE,似然函数:
,其中
及
似然函数两边取对数,方便求导
展开:
在对似然函数中对参数b求偏导
在对似然函数中对参数c求偏导
其中,对于c的偏导数为0最好解,将抽样结果 83.4005,91.5985和65.7138带入(很明显,就是取抽样均值时,c的偏导为0):
将c=80.2376带入,再令b的偏导数为0,有
解得:
因此利用在3样本采样下,利用MLE,我们推测出概率密度函数最有可能的样子,即最大似然估计的概率密度函数为:
上帝给的真实概率密度函数为:
这差距还挺大啊,哈哈哈,因为要手算,所以我只抽样了三个样本啊,接下来让MATLAB秘书帮我们自动化地计算采样100、1000、和10000下的基于MLE的概率密度函数。
%% 设置均值和方差
mu = 80;
sigma_squared = 40;
sigma = sqrt(sigma_squared); % 标准差是方差的平方根% 随机生成100个样本
num_samples = 100;
samples = normrnd(mu, sigma, [num_samples, 1]);%%将计算的偏导数,进行自动化计算%1。求解c的偏导
c=mean(samples);
%2.求解b的偏导,利用了自定义的函数
b = solve_for_b_explicit(samples, c);disp([num2str((b/pi)^(1/2)),'*e^(',num2str(-b),'(x-',num2str(c),'))'])function b = solve_for_b_explicit(x, c)% 输入:% x - 输入数组% c - 已知常数%% 输出:% b - 求解的值% 计算输入数组的元素个数n = length(x);% 计算求和部分sum_xi_minus_c_squared = sum((x - c).^2);% 计算b的显式解b = n / (2 * sum_xi_minus_c_squared);
end采样数量为10时:0.044206*e^(-0.0061392(x-76.8192)^2)
采样数量为50时:0.072282*e^(-0.016414(x-80.4277)^2)
采样数量为100时:0.05551*e^(-0.0096803(x-80.1956)^2)
采样数量为500时:0.064705*e^(-0.013153(x-80.2877)^2)
采样数量为1000时:0.062513*e^(-0.012277(x-79.9881)^2)
采样数量为10000时:0.06283*e^(-0.012402(x-80.0022)^2)
真实概率密度分布函数:0.631*e^(-0.0125(x-80 )^2)
可以发现,随着采样数量的增加,最大似然估计的分布函数越来越准确!
总结:
通过详细的推导过程和问题的实践,我们可以很好的掌握MLE的基本思想和基础理论。在本篇文章中,我们在不知道正太分布概率密度分布函数的背景下,仍利用MLE拟合出了具体的数值表达式,可见MLE对数据分布的强大拟合能力。
MLE是信息论和机器学习的重要方法,比如:在隐马尔可夫模型(HMM)等序列数据建模中,MLE通过Baum-Welch算法(一种特殊的期望最大化EM算法)来迭代地优化模型参数。
相关文章:
底层逻辑之:极大似然方法(Maximum Likelihood Estimation, MLE)
简介: 极大似然方法(Maximum Likelihood Estimation, MLE)是一种用于估计统计模型参数的方法。其核心思想是基于观测数据来寻找最可能产生这些数据的模型参数。 早在1821年,德国数学家高斯(C. F. Gauss)就…...

笔记:Centos Nginx Jdk Mysql OpenOffce KkFile Minio安装部署
远程工具 ToDesk Nginx 解压 tar zxvf nginx-1.20.2.tar.gz进入Nginx 文件夹 cd nginx-1.20.2报错解决 ./configure: error: C compiler cc is not found yum -y install gcc gcc-c autoconf automake make./configure: error: the HTTP rewrite module requires the PC…...

【MARL】深入理解多智能体近端策略优化(MAPPO)算法与调参
📢本篇文章是博主强化学习(RL)领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅…...

深入探索Go语言中的sync.Mutex与sync.RWMutex:原理、应用与实践
深入探索Go语言中的sync.Mutex与sync.RWMutex:原理、应用与实践 在并发编程的世界里,Go语言以其独特的并发模型和简洁的语法赢得了广泛的关注。在Go语言的并发控制工具箱中,sync.Mutex和sync.RWMutex是两个至关重要的工具,它们帮助开发者保护共享资源,避免竞态条件,确保…...

15.postgresql--jsonb 数组进行打平,过滤
用jsonb_array_elements函数先展开数组,再用jsonb_each函数遍历元素中的键值对 例如: SELECT * FROM data_table, LATERAL jsonb_array_elements(json_column) WITH ORDINALITY as elem(element, idx) JOIN LATERAL jsonb_each(elem.element) as kv(ke…...

linux下i2c开发与框架源码分析
目录 1 概述 2 I2c子系统框架 3 I2C的使用流程 3.1 在驱动里使用 3.2 在应用层使用 3.3 I2ctool的使用 4 为硬件i2c注册一个适配器 5 i2c子系统源码流程分析 5.1 i2c device与driver绑定过程 5.1.1 Driver的注册与处理 5.1.2 Client device的生成 5.2 I2c的发送与接…...

[ruby on rails] 安装docker
1. docker安装 ubuntu14.04后自带docker安装包,可以直接安装docker.io sudo apt-get updatesudo apt-get install -y docker.io # 安装后启动sudo service docker start最新版本docker 安装docker-ce # 官方源 curl -fsSL https://download.docker.com/linux/ubun…...

I2C学习
详情学习 12. I2C通讯 — [野火]Linux基础与应用开发实战指南——基于LubanCat-RK系列板卡 文档 (embedfire.com) 问题 i2c总线中scl和sda两条线的作用以及区别 在 I2C 总线(Inter-Integrated Circuit)中,SCL 和 SDA 是两条核心信号线&am…...

VUE:基于MVVN的前端js框架
文章目录 vue框架v-show vue框架 注意是 先写函数名,再写function。 handle:function (){}下面是错误的 function:handle(){}3 v-show 本质上等于号后面还是判断条件,所以不能写赋值语句,下面是正确的 下面是错误的 v-show " ge…...

06、Spring AOP
在我们接下来聊Spring AOP之前我们先了解一下设计模式中的代理模式。 一、代理模式 代理模式是23种设计模式中的一种,它属于结构型设计模式。 对于代理模式的理解: 程序中对象A与对象B无法直接交互,如:有人要找某个公司的老总得先打前台登记传达程序中某个功能需要在原基…...

c语言学习26字符串的应用
字符串在stm32串口中的应用 串口控制流水灯 pc通过串口发送字符串命令控制流水灯 open 流水灯打开 close 流水灯关闭 speed 1~9速度控制 if(strcmp((char *)usart1_rec_buff,"open")0) { led_flag 1; } else if(strcmp((char *)usart1_rec_buff,"close&qu…...

法语旅游常用口语-柯桥学外语到蓝天广场泓畅学校
以下是一些实用的法语旅游常用口语,帮助你在法国旅行时能够进行基本的交流: 问候与道别 Bonjour: 用于日常问候。Au revoir: 用于告别。 请求帮助 S’il vous plat: 用于请求帮助,例如在需要寻找某个地点或服务时。 询问信息 Excusez-moi: 用…...

Kafka 生产者优化与数据处理经验
Kafka:分布式消息系统的核心原理与安装部署-CSDN博客 自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例-CSDN博客 Kafka 生产者全面解析:从基础原理到高级实践-CSDN博客 Kafka 生产者优化与数据处理经验-CSDN博客 Kafka 工作流程解析:…...
MySQL 主从复制之多线程复制
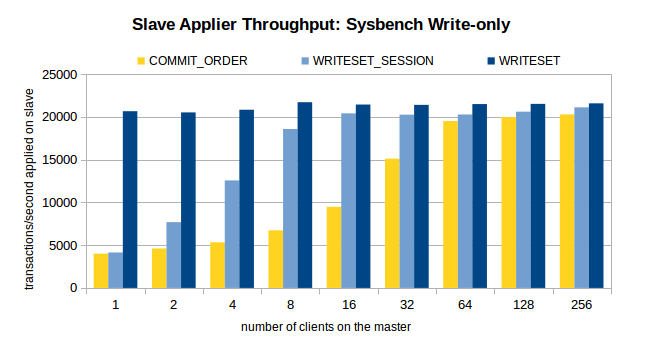
一、MySQL 多线程复制的背景 MySQL 的主从复制延迟一直是受开发者最为关注的问题之一,MySQL 从 5.6 版本开始追加了并行复制功能,目的就是为了改善复制延迟问题,并行复制称为enhanced multi-threaded slave(简称MTS)。…...

Linux2.6内核进程调度队列
文章目录 前言运行队列 runqueue优先级活动队列过期队列活跃队列 VS 过期队列active指针和expired指针O(1)调度算法 前言 在前面学习并认识了进程之后,我们会发出一个疑问:Linux内核是如何调度进程的呢? 接下来我们就以Linux2.6内核为例深入探…...

Infineon(英飞凌) TLE985xQX 芯片电机工作电流、电压AD采样
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 单片机芯片合集 文章目录 其他系列文章导航 文章目录 前言 一、选取合适的端口 1.通过 OP1、OP2 电流采集运放输入端口进行H桥驱动的电流采集。 2.通过 O_D_VBAT_AD_EN、I_A_VBAT_A…...

Sparrow系列拓展篇:对信号量应用问题的深入讨论
前言 笔者之前已经介绍过了Sparrow信号量的源码,但是对于信号量的使用,并没有讲得非常详细,仅仅讲了同步与互斥的概念。 本章让笔者介绍如何使用Sparrow的信号量,深入探讨一下信号量在同步、计数与互斥中的应用。 使用信号量解…...

图文详解Docker下配置、测试Redis
文章目录 前言实测环境:实验思路: 正文1.准备工作2. 配置、运行 Redis 容器3. 配置测试 总结 前言 配置、测试redis数据库服务器,首先确保正确安装docker,并且已启动运行,具体安装docker方法见笔者前面的博文《OpenEu…...

Python编程艺术:优雅与实用的完美平衡(推导式)
在Python这门优雅的编程语言中,处处体现着"简洁即是美"的设计哲学。今天我们深入探讨Python中那些让代码更优雅、更高效的编程技巧,这些技巧不仅能提升代码的可读性,还能让编程过程充满乐趣。 列表推导式的魔力 Python的列表推导…...

Spring Boot框架Starter组件整理
在Spring Boot框架中,starter是一种预定义的依赖集合,旨在简化Maven或Gradle等构建工具中的依赖管理。每个starter都包含了实现特定功能所需的库和组件,以及相应的配置文件。开发者只需在项目中引入相应的starter依赖,即可快速搭建…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
