力扣11.23
1964. 找出到每个位置为止最长的有效障碍赛跑路线
你打算构建一些障碍赛跑路线。给你一个 下标从 0 开始 的整数数组 obstacles ,数组长度为 n ,其中 obstacles[i] 表示第 i 个障碍的高度。
对于每个介于 0 和 n - 1 之间(包含 0 和 n - 1)的下标 i ,在满足下述条件的前提下,请你找出 obstacles 能构成的最长障碍路线的长度:
- 你可以选择下标介于 0 到 i 之间(包含 0 和 i)的任意个障碍。
- 在这条路线中,必须包含第 i 个障碍。
- 你必须按障碍在 obstacles 中的 出现顺序 布置这些障碍。
- 除第一个障碍外,路线中每个障碍的高度都必须和前一个障碍 相同 或者 更高
返回长度为 n 的答案数组 ans ,其中 ans[i] 是上面所述的下标 i 对应的最长障碍赛跑路线的长度。
数据范围
n == obstacles.length1 <= n <= 1051 <= obstacles[i] <= 107
分析
本题数据范围比较大,因此不能使用n方做法,采用贪心+二分的方法,用q数组记录所有长度为i的最长非递减子序列中的最小值,这样可以尽可能多的构造非递减子序列,例如原数组为1,2,3,2
- q=[1]
- q=[1,2]
- q=[1,2,3]
- 2找到第一个大于2的下标,并将其替换q=[1,2,2],此时替换的位置就是最长序列的长度
代码
class Solution {
public:const static int N = 1e5 + 5;int dp[N]; int q[N], tt = -1;void print() {for(int i = 0; i <= tt; i ++ ) cout << q[i] << " ";cout << endl;}vector<int> longestObstacleCourseAtEachPosition(vector<int>& obstacles) {int n = obstacles.size();vector<int> res;res.resize(n);for(int i = 0; i < n; i ++ ) {if(tt == -1 || obstacles[i] >= q[tt]) {q[++ tt] = obstacles[i];res[i] = tt + 1;}else { int pos = upper_bound(q, q + tt, obstacles[i]) - q;res[i] = pos + 1;q[pos] = obstacles[i];}}return res;}
};
2111. 使数组 K 递增的最少操作次数
给你一个下标从 0 开始包含 n 个正整数的数组 arr ,和一个正整数 k 。
如果对于每个满足 k <= i <= n-1 的下标 i ,都有 arr[i-k] <= arr[i] ,那么我们称 arr 是 K 递增 的。
- 比方说,arr = [4, 1, 5, 2, 6, 2] 对于 k = 2 是 K 递增的,因为:
- arr[0] <= arr[2] (4 <= 5)
- arr[1] <= arr[3] (1 <= 2)
- arr[2] <= arr[4] (5 <= 6)
- arr[3] <= arr[5] (2 <= 2)
但是,相同的数组 arr 对于 k = 1 不是 K 递增的(因为 arr[0] > arr[1]),对于 k = 3 也不是 K 递增的(因为 arr[0] > arr[3] )。
每一次 操作 中,你可以选择一个下标 i 并将 arr[i] 改成任意 正整数。
请你返回对于给定的 k ,使数组变成 K 递增的 最少操作次数 。
数据范围
1 <= arr.length <= 1051 <= arr[i], k <= arr.length
分析
实际就是将原数组拆分为k个子数组,对每个子数组求他的最长非递减子序列,然后对于非递减子序列的元素就是最优的需要修改的,统计一下即可,这里求最长非递减子序列也是通过上题的贪心+二分计算
代码
class Solution {
public:const static int N = 1e5 + 5;int dp[N];int q[N], tt = -1;void print() {for(int i = 0; i <= tt; i ++ ) cout << q[tt] << " ";cout << endl;}int kIncreasing(vector<int>& arr, int k) {int res = 0;int n = arr.size();for(int i = 0; i <= k - 1; i ++ ) {tt = -1;int cnt = 0;for(int j = i; j < n; j += k) {cnt ++ ;if(tt == -1 || arr[j] >= q[tt]) q[++ tt] = arr[j];else {int pos = upper_bound(q, q + tt, arr[j]) - q;q[pos] = arr[j];}}res += cnt - (tt + 1);}return res;}
};
1626. 无矛盾的最佳球队
假设你是球队的经理。对于即将到来的锦标赛,你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。
然而,球队中的矛盾会限制球员的发挥,所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于 一名年龄较大的球员,则存在矛盾。同龄球员之间不会发生矛盾。
给你两个列表 scores 和 ages,其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回 所有可能的无矛盾球队中得分最高那支的分数
数据范围
1 <= scores.length, ages.length <= 1000scores.length == ages.length<= scores[i] <= 1061 <= ages[i] <= 1000
分析
首先将球员先按照年龄排序,再按照分数从小到大排序,令dp[i]表示选择第i个球员的最大分数,状态转移如下:
- d p [ i ] = m a x ( d p [ i ] , d p [ j ] + s c o r e [ i ] ) dp[i]=max(dp[i],dp[j]+score[i]) dp[i]=max(dp[i],dp[j]+score[i])
代码
class Solution {
public:const static int N = 1005;int dp[N], agedp[N];struct node_ {int score, age;friend bool operator < (const node_ a, const node_ b) {if(a.age == b.age) return a.score < b.score;return a.age < b.age;}};vector<node_> nodes;int bestTeamScore(vector<int>& scores, vector<int>& ages) {int n = ages.size();for(int i = 0; i < n; i ++ ) {nodes.push_back({scores[i], ages[i]});}sort(nodes.begin(), nodes.end());for(int i = 0; i < n; i ++ ) {dp[i] += nodes[i].score;for(int j = 0; j < i; j ++ ) {if(nodes[j].score <= nodes[i].score) dp[i] = max(dp[i], dp[j] + nodes[i].score);}}int res = 0;for(int i = 0; i < n; i ++ ) res = max(res, dp[i]);return res;}
};
54. 俄罗斯套娃信封问题
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
注意:不允许旋转信封。
数据范围
1 <= envelopes.length <= 105envelopes[i].length == 21 <= wi, hi <= 105
分析
先按w升序,再按h降序,按h降序保证了w相同的信封只能选一个,然后对h求最长上升子序列就行,此时就满足h递增且w递增
代码
class Solution {
public:const static int N = 1e5 + 5;struct node_ {int a, b;friend bool operator < (const node_ &a, const node_ &b) {if(a.a == b.a) return a.b > b.b;return a.a < b.a;}};int n;node_ q[N];int tt = -1;vector<node_> envelopes;int find(node_ x) {int l = 0, r = tt;while(l < r) {int mid = (l + r) >> 1;if(q[mid].b < x.b) l = mid + 1;else r = mid;}return l;}int maxEnvelopes(vector<vector<int>>& envs) {n = envs.size();for(int i = 0; i < n; i ++ ) envelopes.push_back({envs[i][0], envs[i][1]});sort(envelopes.begin(), envelopes.end());for(int i = 0; i < n; i ++ ) {int a = envelopes[i].a, b = envelopes[i].b;if(tt == -1 || b > q[tt].b) q[++ tt] = {a, b};else {int pos = find({a, b});q[pos] = {a, b};}}return tt + 1;}
};
相关文章:

力扣11.23
1964. 找出到每个位置为止最长的有效障碍赛跑路线 你打算构建一些障碍赛跑路线。给你一个 下标从 0 开始 的整数数组 obstacles ,数组长度为 n ,其中 obstacles[i] 表示第 i 个障碍的高度。 对于每个介于 0 和 n - 1 之间(包含 0 和 n - 1&…...

golang实现TCP服务器与客户端的断线自动重连功能
1.服务端 2.客户端 生成服务端口程序: 生成客户端程序: 测试断线重连: 初始连接成功...

数据结构 (6)栈的应用举例
1. 递归调用 递归函数在执行时,会将每一层的函数调用信息(包括局部变量、参数和返回地址)存储在栈中。当递归函数返回时,这些信息会从栈中弹出,以便恢复之前的执行状态。栈的后进先出(LIFO)特性…...
)
谁的年龄最小(结构体专题)
题目描述 设计一个结构体类型,包含姓名、出生日期。其中出生日期又包含年、月、日三部分信息。输入n个好友的信息,输出年龄最小的好友的姓名和出生日期。 输入描述 首先输入一个整数n(1<n<10),表示好友人数,然后输入n行&…...

【论文笔记】LLaVA-KD: A Framework of Distilling Multimodal Large Language Models
Abstract 大语言模型(Large Language Models, LLM)的成功,使得研究者为了统一视觉和语言的理解去探索多模态大预言模型(Multimodal Large Language Models, MLLM)。 但是MLLM庞大的模型和复杂的计算使其很难应用在资源受限的环境,小型MLLM(s-MLLM)的表现…...

M|大脑越狱
rating: 7.0 豆瓣: 7.6 上映时间: “2015” 类型: M悬疑 导演: 约瑟夫怀特 Joseph White 主演: 亚历山大欧文 Alexander Owen爱德华富兰克林 Edward Franklin 国家/地区: 英国 片长/分钟: 20分钟 M|大脑越狱 想法不错,但是逻辑比较一般。属于…...
)
数据库编程(sqlite3)
一:数据库分类 常用的数据库 大型数据库 :Oracle商业、多平台、关系型数据库功能最强大、最复杂、市场占比最高的商业数据库 中型数据库 :Server是微软开发的数据库产品,主要支持windows平台 小型数据库 : mySQL是一个小型关系型…...

【C语言】关键字详解
【C语言】关键字详解 文章目录 [TOC](文章目录) 前言一、char1.定义字符串类型2.定义字符类型 二、short三、int四、long五、signed六、unsigned七、float八、double九、struct、union、enum十、void1.void用于函数声明,没有返回值的函数,其类型为 void。…...

什么是计算机网络
什么是计算机网络? 计算机网络的定义计算机网络的分类按覆盖范围分类按拓扑结构分类按通信传输介质分类按信号频带占用方式分类 计算机网络的功能信息交换资源共享分布式处理 计算机网络的组成计算机网络的定义计算机网络的分类按覆盖范围分类按拓扑结构分类按通信传…...

【大数据学习 | Spark-Core】Spark的分区器(HashPartitioner和RangePartitioner)
之前学过的kv类型上面的算子 groupby groupByKey reduceBykey sortBy sortByKey join[cogroup left inner right] shuffle的 mapValues keys values flatMapValues 普通算子,管道形式的算子 shuffle的过程是因为数据产生了打乱重分,分组、排序、join等…...
)
CSS3_BFC(十二)
BFC MDN对BFC的解释:块格式化上下文(Block Formating Context, BFC)是web页面的可视CSS渲染的一部分,是块盒子的布局过程发生的区域,也是浮动元素与其他元素交互的区域。 1、开启BFC flow-root对内容的影响是最低的&am…...

C0032.在Clion中使用MSVC编译器编译opencv的配置方法
使用MSVC编译器编译opencv的配置方法...

微信小程序中会议列表页面的前后端实现
题外话:想通过集成腾讯IM来解决即时聊天的问题,如果含语音视频,腾讯组件一年5万起步,贵了!后面我们改为自己实现这个功能,这里只是个总结而已。 图文会诊需求 首先是个图文列表界面 同个界面可以查看具体…...

WEB攻防-通用漏洞文件上传二次渲染.htaccess变异免杀
知识点: 1、文件上传-二次渲染 2、文件上传-简单免杀变异 3、文件上传-.htaccess妙用 4、文件上传-PHP语言特性 1、上传后门时,文件内容带.就不行 这时可以上传一个转换后的ip地址,ip地址对应网站包含后门代码 转换后的int会在访问的时候…...

vue实现列表滑动下拉加载数据
一、实现效果 二、实现思路 使用滚动事件监听器来检测用户是否滚动到底部,然后加载更多数据 监听滚动事件。检测用户是否滚动到底部。加载更多数据。 三、案例代码 <div class"drawer-content"><div ref"loadMoreTrigger" class&q…...

全面解析:HTML页面的加载全过程(四)--浏览器渲染之样式计算
主线程遍历得到的 DOM 树,依次为树中的每个节点计算出它最终的样式,称之为 Computed Style。 通过前面生成的DOM 树和 CSSOM 树,遍历 DOM 树,为每一个 DOM 节点,计算它的所有 CSS 属性,最后会得到一棵带有…...

#Verilog HDL# 谈谈代码中如何跨层次引用
目录 一 先谈作用问题 二 再谈跨层次问题 2.1 向下引用 2.2 向上引用 一 先谈作用问题 大多数编程语言都有一个称为作用域(scope)的特征,它定义了代码的某些部分对于变量和方法的可见性。作用域定义了一个命名空间,以避免同一命名空间内不同对象名称之间的冲突。 V…...

LeetCode 每日一题 2024/11/18-2024/11/24
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 11/18 661. 图片平滑器11/19 3243. 新增道路查询后的最短距离 I11/20 3244. 新增道路查询后的最短距离 II11/21 3248. 矩阵中的蛇11/22 3233. 统计不是特殊数字的数字数量1…...
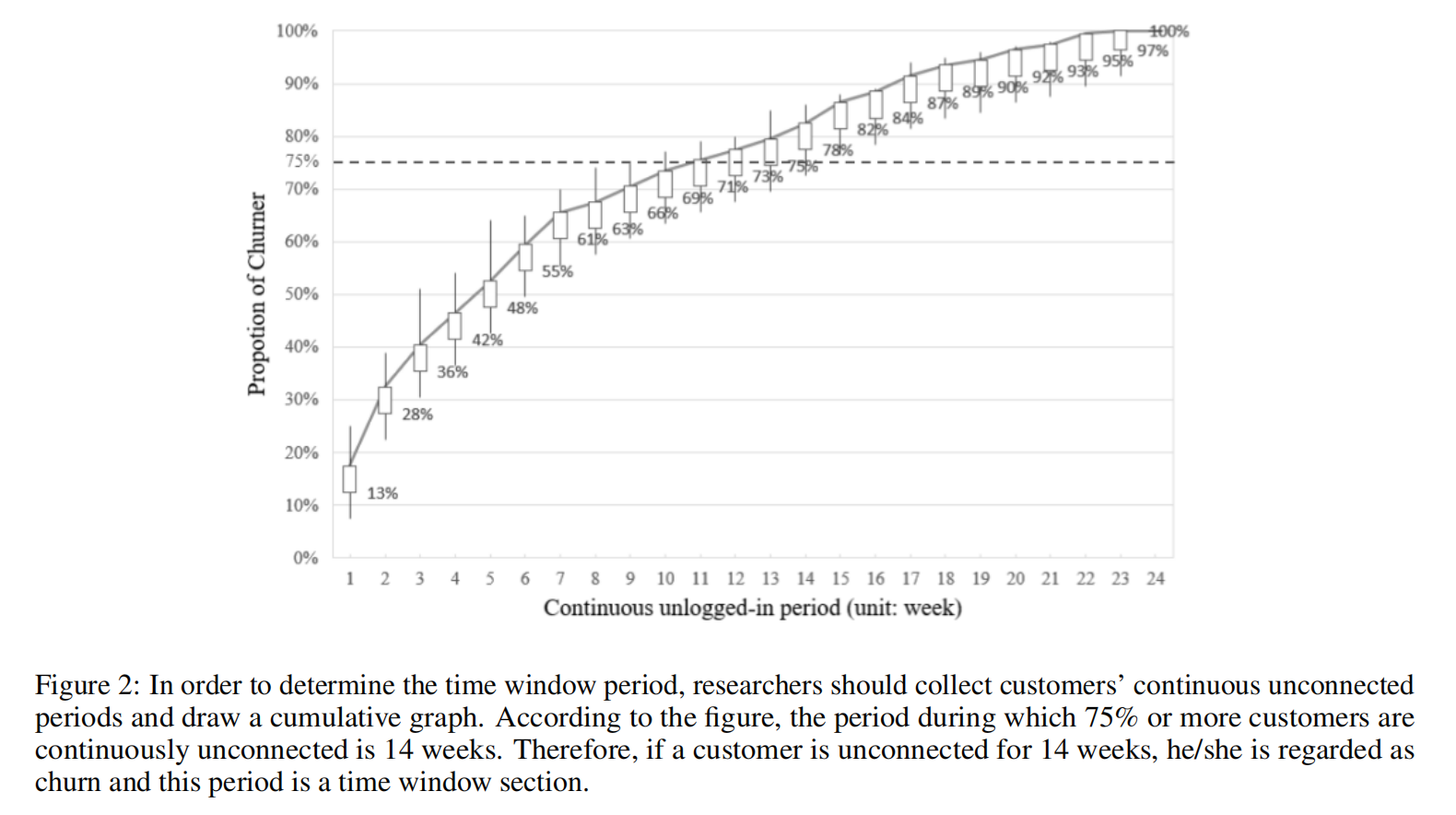
客户流失分析综述
引言 客户流失这个术语通常用来描述在特定时间或合同期内停止与公司进行业务往来的客户倾向性[1]。传统上,关于客户流失的研究始于客户关系管理(CRM)[2]。在运营服务时,防止客户流失至关重要。过去,客户获取相对于流失…...

基于51单片机的红包抽奖proteus仿真
地址: https://pan.baidu.com/s/1nYZlLb64kdZAWSydT_uHfA 提取码:1234 仿真图: 芯片/模块的特点: AT89C52/AT89C51简介: AT89C52/AT89C51是一款经典的8位单片机,是意法半导体(STMicroelectro…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
