学习日记_20241123_聚类方法(MeanShift)
前言
提醒:
文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。
其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展及意见建议,欢迎评论区讨论交流。
文章目录
- 前言
- 聚类算法
- 经典应用场景
- Mean Shift
- 优点:
- 缺点:
- 总结:
- 简单实例(函数库实现)
- 数学表达
- 总结
- 手动实现
- 代码分析
聚类算法
聚类算法在各种领域中有广泛的应用,主要用于发现数据中的自然分组和模式。以下是一些常见的应用场景以及每种算法的优缺点:
经典应用场景
-
市场细分:根据消费者的行为和特征,将他们分成不同的群体,以便进行有针对性的营销。
-
图像分割: 将图像划分为多个区域或对象,以便进行进一步的分析或处理。
-
社交网络分析:识别社交网络中的社区结构。
-
文档分类:自动将文档分组到不同的主题或类别中。
-
异常检测识别数据中的异常点或异常行为。
-
基因表达分析:在生物信息学中,根据基因表达模式对基因进行聚类。
Mean Shift
Mean Shift 是一种基于密度的聚类方法,旨在寻找数据点的高密度区域,并将其聚集成簇。以下是 Mean Shift 的优缺点:
优点:
- 无参数: Mean Shift 不需要预先指定簇的数量,这使得它在处理未知数据时更具灵活性。
- 适应性: Mean Shift 根据数据的分布自适应地确定簇的形状和大小,能够处理不同密度的簇。
- 有效处理非球形簇: 它能够识别和聚类形状各异的簇,而不仅限于圆形或球形。
- 不受噪声影响: Mean Shift 对噪声的鲁棒性较强,这使得它在某些应用中表现良好。
- 可解释性: 由于该算法基于数据的密度估计,因此可以清晰地理解每个簇的形成过程。
缺点:
- 计算复杂度高: Mean Shift 的计算复杂度通常较高,尤其是在大数据集上,因为每次迭代都需要计算所有点之间的距离。
- 选择带宽参数: Mean Shift 的效果在很大程度上依赖于带宽参数的选择,选择不当可能导致不理想的聚类结果。带宽过小可能导致过拟合,而过大可能导致聚类的缺乏细节。
- 对高维数据敏感: 在高维空间中,密度估计变得更加困难,Mean Shift 的效果可能不如在低维空间中显著。
- 收敛速度: Mean Shift 的收敛速度可能在某些情况下较慢,特别是在数据点分布非常稀疏的情况下。
- 局部极小问题: 在某些情况下,Mean Shift 可能收敛到局部极小值,而不是全局最优聚类解决方案。
总结:
Mean Shift 是一种强大且灵活的聚类算法,尤其适合于处理具有复杂形状和不同密度的簇。然而,它的计算效率和对参数设置的敏感性可能会限制其在某些应用中的有效性。在选择使用 Mean Shift 时,需考虑数据的特性和应用场景,以决定其适用性。
简单实例(函数库实现)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift# 生成样本数据
n_samples = 1000
X, y = make_blobs(n_samples=n_samples, centers=3, cluster_std=0.60, random_state=0)# 使用 Mean Shift 进行聚类
mean_shift = MeanShift(bandwidth=1.5) # 选择带宽参数
mean_shift.fit(X)# 获取聚类标签和中心
labels = mean_shift.labels_
cluster_centers = mean_shift.cluster_centers_# 输出聚类结果
n_clusters = len(np.unique(labels))
print(f"聚类数量: {n_clusters}")# 绘制聚类结果
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30, cmap='viridis', marker='o', edgecolor='k')
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], c='red', s=200, alpha=0.75, marker='X') # 聚类中心
plt.title('Mean Shift Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.show()data数据分布与代码运行结果:
数学表达
Mean Shift 是一种基于密度的聚类算法,其核心思想是通过迭代地向数据点的密度最大区域移动来进行聚类。以下是对 Mean Shift 方法的数学解释和公式推导。
- 核密度估计
Mean Shift 的主要步骤是首先进行核密度估计(Kernel Density Estimation,KDE),以得到数据点的密度分布。给定数据集 X = { x 1 , x 2 , … , x n } X = \{x_1, x_2, \ldots, x_n\} X={x1,x2,…,xn},我们可以使用核函数 K K K 来估计某一点 x x x 的密度:
f ^ ( x ) = 1 n ∑ i = 1 n K ( x − x i h ) \hat{f}(x) = \frac{1}{n} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right) f^(x)=n1i=1∑nK(hx−xi)
其中:
- f ^ ( x ) \hat{f}(x) f^(x) 是在点 x x x 的估计密度。
- h h h 是带宽参数,控制核的宽度。
- K K K 是核函数,常用的有高斯核、均匀核等。
- Mean Shift 迭代步骤
Mean Shift 的目标是通过移动数据点来找到密度的极大值。对每个数据点 x x x,Mean Shift 更新的公式为:
m h ( x ) = ∑ i = 1 n x i K ( x − x i h ) ∑ i = 1 n K ( x − x i h ) m_h(x) = \frac{\sum_{i=1}^{n} x_i K\left(\frac{x - x_i}{h}\right)}{\sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right)} mh(x)=∑i=1nK(hx−xi)∑i=1nxiK(hx−xi)
其中:
- m h ( x ) m_h(x) mh(x) 是在 x x x 位置的 Mean Shift 矢量,表示对 x x x 的更新。
- 该公式表示在当前位置 x x x 周围的所有点 x i x_i xi 的加权平均。
- 更新规则
Mean Shift 的更新过程可以概括如下:
- 计算当前点 x x x 的密度加权平均位置 m h ( x ) m_h(x) mh(x)。
- 更新 x x x 为 m h ( x ) m_h(x) mh(x)。
- 重复步骤 1 和 2,直到 x x x 的变化小于某个预设的阈值(即收敛)。
- 收敛和聚类
通过不断更新,每个点将最终收敛到一个高密度区域(即簇的中心)。在所有点收敛后,可以通过其聚类标签来区分不同的簇,通常使用每个点最终对应的中心位置来标识。- 聚类结果
最终的聚类结果基于每个点所收敛的中心位置。相同的聚类中心将被标记为同一簇。聚类的数量不是预先指定的,而是在算法运行后自动确定的。总结
Mean Shift 聚类通过不断地向数据点密度最大化的方向移动,利用核密度估计来找到数据的高密度区域。其数学基础主要依赖于核函数和加权平均的概念,使其能够灵活地适应不同密度和形状的簇。选择合适的带宽参数 h h h 是影响 Mean Shift 效果的重要因素。
手动实现
import numpy as npdef gaussian_kernel(distance, bandwidth):"""高斯核函数。参数:- distance: 距离值- bandwidth: 带宽参数返回:- 核函数的值"""return (1 / (bandwidth * np.sqrt(2 * np.pi))) * np.exp(-0.5 * (distance / bandwidth) ** 2)def mean_shift(data, bandwidth, max_iter=300, tol=1e-3):"""Mean Shift 聚类算法实现。参数:- data: 输入数据点,形状为 (n_samples, n_features)- bandwidth: 带宽参数,控制核的范围- max_iter: 最大迭代次数- tol: 收敛判定的容忍度返回:- centers: 聚类中心- labels: 数据点的标签"""# 初始化:所有点都是初始聚类中心centers = np.copy(data)for it in range(max_iter):new_centers = []for center in centers:# 计算到其他点的距离distances = np.linalg.norm(data - center, axis=1)# 计算核函数权重weights = gaussian_kernel(distances, bandwidth)# 更新中心点位置new_center = np.sum(data * weights[:, np.newaxis], axis=0) / np.sum(weights)new_centers.append(new_center)# 检查是否收敛new_centers = np.array(new_centers)shift_distance = np.linalg.norm(new_centers - centers, axis=1).max()centers = new_centersif shift_distance < tol:break# 将靠近的中心合并unique_centers = []for center in centers:if not any(np.linalg.norm(center - unique_center) < bandwidth / 2 for unique_center in unique_centers):unique_centers.append(center)unique_centers = np.array(unique_centers)# 为每个点分配标签labels = np.zeros(len(data), dtype=int)for i, point in enumerate(data):distances = np.linalg.norm(unique_centers - point, axis=1)labels[i] = np.argmin(distances)return unique_centers, labels# 测试代码
if __name__ == "__main__":# 生成测试数据np.random.seed(0)data = np.vstack((np.random.normal(loc=0, scale=1, size=(50, 2)),np.random.normal(loc=5, scale=1, size=(50, 2)),np.random.normal(loc=10, scale=1, size=(50, 2))))# 调用 Mean Shiftbandwidth = 2 # 带宽参数centers, labels = mean_shift(data, bandwidth)# 可视化import matplotlib.pyplot as pltplt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis', s=30)plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=100, label='Centers')plt.legend()plt.title("Mean Shift Clustering")plt.show()数据与结果为:
代码分析
def gaussian_kernel(distance, bandwidth):"""高斯核函数。参数:- distance: 距离值- bandwidth: 带宽参数返回:- 核函数的值"""return (1 / (bandwidth * np.sqrt(2 * np.pi))) * np.exp(-0.5 * (distance / bandwidth) ** 2)
代码的数学表达式可以通过以下公式表示:
K ( x ) = 1 σ 2 π exp ( − x 2 2 σ 2 ) K(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left(-\frac{x^2}{2\sigma^2}\right) K(x)=σ2π1exp(−2σ2x2)
其中:
- K ( x ) K(x) K(x) 是高斯核函数的值。
- σ \sigma σ 是带宽参数 h h h(在此处带入
bandwidth)。- x x x 是距离值(在此处带入
distance)。
将其转换为数学表达式,我们可以写成:
K ( distance ) = 1 bandwidth ⋅ 2 π exp ( − 1 2 ( distance bandwidth ) 2 ) K(\text{distance}) = \frac{1}{\text{bandwidth} \cdot \sqrt{2\pi}} \exp\left(-\frac{1}{2} \left(\frac{\text{distance}}{\text{bandwidth}}\right)^2\right) K(distance)=bandwidth⋅2π1exp(−21(bandwidthdistance)2)
这表达了在给定距离和带宽参数的情况下,高斯核函数的值。它描述了如何根据距离值和带宽来计算核函数的输出,形成一个用于加权的函数。
def mean_shift(data, bandwidth, max_iter=300, tol=1e-3):"""Mean Shift 聚类算法实现。参数:- data: 输入数据点,形状为 (n_samples, n_features)- bandwidth: 带宽参数,控制核的范围- max_iter: 最大迭代次数- tol: 收敛判定的容忍度返回:- centers: 聚类中心- labels: 数据点的标签"""# 初始化:所有点都是初始聚类中心centers = np.copy(data)for it in range(max_iter):new_centers = []for center in centers:# 计算到其他点的距离distances = np.linalg.norm(data - center, axis=1)# 计算核函数权重weights = gaussian_kernel(distances, bandwidth)# 更新中心点位置new_center = np.sum(data * weights[:, np.newaxis], axis=0) / np.sum(weights)new_centers.append(new_center)# 检查是否收敛new_centers = np.array(new_centers)shift_distance = np.linalg.norm(new_centers - centers, axis=1).max()centers = new_centersif shift_distance < tol:break# 将靠近的中心合并unique_centers = []for center in centers:if not any(np.linalg.norm(center - unique_center) < bandwidth / 2 for unique_center in unique_centers):unique_centers.append(center)unique_centers = np.array(unique_centers)# 为每个点分配标签labels = np.zeros(len(data), dtype=int)for i, point in enumerate(data):distances = np.linalg.norm(unique_centers - point, axis=1)labels[i] = np.argmin(distances)return unique_centers, labels
centers = np.copy(data)
给定数据集 { x 1 , x 2 , … , x n } ⊂ R d \{x_1, x_2, \ldots, x_n\} \subset \mathbb{R}^d {x1,x2,…,xn}⊂Rd。
初始聚类中心设定为: C = { c 1 , c 2 , … , c n } = { x 1 , x 2 , … , x n } C = \{c_1, c_2, \ldots, c_n\} = \{x_1, x_2, \ldots, x_n\} C={c1,c2,…,cn}={x1,x2,…,xn}。centers = np.copy(data)
for it in range(max_iter):
- 权重计算(核函数权重):
- 对每个点 x i ∈ R d x_i \in \mathbb{R}^d xi∈Rd,计算相对于当前中心 c j c_j cj 的距离: d ( x i , c j ) = ∥ x i − c j ∥ d(x_i, c_j) = \|x_i - c_j\| d(xi,cj)=∥xi−cj∥。
- 使用核函数计算权重,通常使用高斯核:
K ( x ) = exp ( − ∥ x ∥ 2 2 h 2 ) K(x) = \exp\left(-\frac{\|x\|^2}{2h^2}\right) K(x)=exp(−2h2∥x∥2)
其中, h h h 是带宽参数。
- 更新聚类中心:
对每个中心 c j c_j cj,根据核权重来更新:
c j new = ∑ i = 1 n K ( x i − c j ) ⋅ x i ∑ i = 1 n K ( x i − c j ) c_j^{\text{new}} = \frac{\sum_{i=1}^n K(x_i - c_j) \cdot x_i}{\sum_{i=1}^n K(x_i - c_j)} cjnew=∑i=1nK(xi−cj)∑i=1nK(xi−cj)⋅xi- 收敛判定:
计算所有中心的最大移动距离:
shift_distance = max j ∥ c j new − c j ∥ \text{shift\_distance} = \max_j \|c_j^{\text{new}} - c_j\| shift_distance=jmax∥cjnew−cj∥
如果 shift_distance < tol \text{shift\_distance} < \text{tol} shift_distance<tol,则算法收敛,否则继续迭代。unique_centers = []
for center in centers:
合并近似中心:
如果两个中心 c i c_i ci 和 c j c_j cj 的距离小于 h 2 \frac{h}{2} 2h,则合并这两个中心。labels = np.zeros(len(data), dtype=int)
for i, point in enumerate(data):
分配标签:
对于每个数据点 x i x_i xi,计算到每个中心的距离,并分配到最近的中心:
label i = arg min k ∥ x i − unique_center k ∥ \text{label}_i = \arg\min_k \|x_i - \text{unique\_center}_k\| labeli=argkmin∥xi−unique_centerk∥
相关文章:

学习日记_20241123_聚类方法(MeanShift)
前言 提醒: 文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。 其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展…...

AI编程和AI绘画哪个更适合创业?
AI编程和AI绘画各有优势,适合创业的方向取决于你的资源、兴趣、市场需求和技术能力。以下是两者的对比分析,帮助你选择更适合的方向: AI编程 优势 1、广泛应用领域: 涉及自动化、数据分析、自然语言处理、计算机视觉等多个领域&a…...

macOS 无法安装第三方app,启用任何来源的方法
升级新版本 MacOS 后,安装下载的软件时,不能在 ”安全性与隐私” 中找不到 ”任何来源” 选项。 1. 允许展示任何来源 点击 启动器 (Launchpad) – 其他 (Other) – 终端 (Terminal): 打开终端后,输入以下代码回车: …...

关于SpringBoot集成Kafka
关于Kafka Apache Kafka 是一个分布式流处理平台,广泛用于构建实时数据管道和流应用。它能够处理大量的数据流,具有高吞吐量、可持久化存储、容错性和扩展性等特性。 Kafka一般用作实时数据流处理、消息队列、事件架构驱动等 Kafka的整体架构 ZooKeeper:…...

4.STM32之通信接口《精讲》之IIC通信---软件实现IIC《深入浅出》面试必备!
接下正式,进入软件编写IIC时序了,并实现对MPU6050的控制,既然是软件实现,那么硬件方面,我仅需两根控制线即可,即:数据控制线SDA,时钟控制线SCL。(人为软件层面定义的&…...

6G通信技术对比5G有哪些不同?
6G,即第六代移动通信技术,是5G之后的延伸,代表了一种全新的通信技术发展方向。与5G相比,6G在多个方面都有显著的不同和提升,以下是对6G通信技术及其与5G差异的详细分析: 一、6G的基本特点 更高的传输速率…...

「Mac玩转仓颉内测版28」基础篇8 - 元组类型详解
本篇将介绍 Cangjie 中的元组类型,包括元组的定义、创建、访问、数据解构以及应用场景,帮助开发者掌握元组类型的使用。 关键词 元组类型定义元组创建元组访问数据解构应用场景 一、元组类型概述 在 Cangjie 中,元组是一种用于存储多种数据…...

WebStorm 2024.3/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理
WebStorm 2024.3/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理 1. 标题识别elementUI组件爆红 这个原因是: 在官网说明里,才版本2024.1开始,默认启用的 Vue Language Server,但是在 Vue 2 项目…...

机械设计学习资料
免费送大家学习资源,已整理好,仅供学习 下载网址: https://www.zzhlszk.com/?qZ02-%E6%9C%BA%E6%A2%B0%E8%AE%BE%E8%AE%A1%E8%A7%84%E8%8C%83SOP.zip...

Python 快速入门(上篇)❖ Python 字符串
Python 字符串 字符串格式化输出字符串拼接获取字符串长度字符串切片字符串处理方法 字符串格式化输出 name “xhx” age 30 # 方法1 print("我的名字是%s,今年%s岁了。 " % (name, age)) # 方法2 print(f"我的名字是{name},今年{age}岁了。")字符串拼接…...

Ubuntu中使用多版本的GCC
我的系统中已经安装了GCC11.4,在安装cuda时出现以下错误提示: 意思是当前的GCC版本过高,要在保留GCC11.4的同时安装GCC9并可以切换,可以通过以下步骤实现: 步骤 1: 安装 GCC 9 sudo apt-get update sudo apt-get ins…...

1+X应急响应(网络)文件包含漏洞:
常见网络攻击-文件包含漏洞&命令执行漏洞: 文件包含漏洞简介: 分析漏洞产生的原因: 四个函数: 产生漏洞的原因: 漏洞利用条件: 文件包含: 漏洞分类: 本地文件包含: …...
)
机器学习实战记录(1)
决策树——划分数据集 def splitDataSet(dataSet, axis, value): retDataSet [] #创建返回的数据集列表for featVec in dataSet: #遍历数据集if featVec[axis] value:reducedFeatVec featVec[:axis] #去掉axis特征reducedFeatVec.extend(featVec[axis1…...

PHP8解析php技术10个新特性
PHP8系列是 PHP编程语言的最新主线版本,带来了许多激动人心的新特性和改进。作为一名PHP开发者,了解这些更新能够帮助你编写更高效、安全和现代的代码。 8的核心技术知识点,包括语言特性、性能优化、安全增强以及开发者工具的改进。 Just-In…...

C++模版特化和偏特化
什么是模版特化 特化的含义:所谓特化,就是将泛型搞得具体化一些,从字面上来解释,就是为已有的模板参数进行一些使其特殊化的指定,使得以前不受任何约束的模板参数,或受到特定的修饰(例如const或…...
Simulink中Model模块的模型保护功能
在开发工作过程中,用户为想要知道供应商的开发能力,想要供应商的模型进行测试。面对如此要求,为了能够尽快拿到定点项目,供应商会选择一小块算法或是模型以黑盒的形式供客户测试。Simulink的Model模块除了具有模块引用的功能之外&…...
:文本编辑器的使用)
Linux常用工具的使用(2):文本编辑器的使用
实验题目:Linux常用工具的使用(2):文本编辑器的使用 实验目的: (1)理解文本编辑器vi的工作模式; (2)掌握文本编辑器的使用方法 实验内容: &a…...

【StarRocks】starrocks 3.2.12 【share-nothing】 多Be集群容器化部署
文章目录 一. 集群规划二.docker compose以及启动脚本卷映射对于网络环境变量 三. 集群测试用户新建、赋权、库表初始化断电重启扩容 BE 集群 一. 集群规划 部署文档 https://docs.starrocks.io/zh/docs/2.5/deployment/plan_cluster/ 分类描述FE节点1. 主要负责元数据管理、…...
联想ThinkServer服务器主要硬件驱动下载
联想ThinkServer服务器主要硬件驱动下载: 联想ThinkServer服务器主要硬件Windows Server驱动下载https://newsupport.lenovo.com.cn/commonProblemsDetail.html?noteid156404#D50...
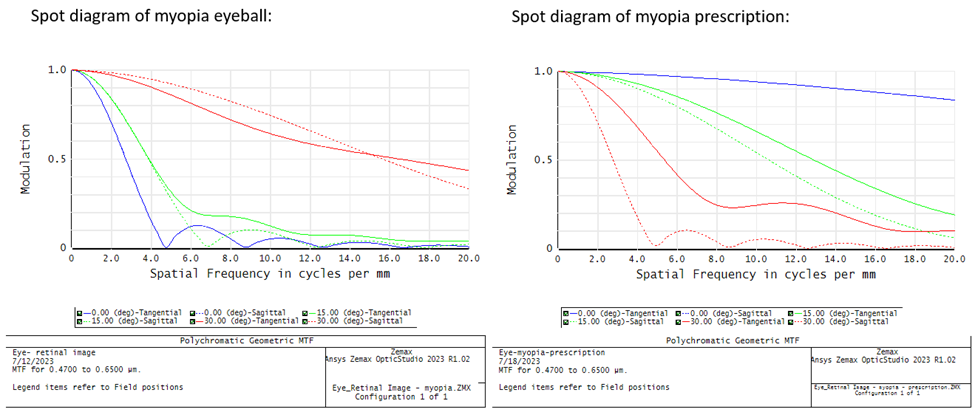
Ansys Zemax Optical Studio 中的近视眼及矫正
近视,通常称为近视眼,是一种眼睛屈光不正,导致远处物体模糊,而近处物体清晰。这是一种常见的视力问题,通常发生在眼球过长或角膜(眼睛前部清晰的部分)过于弯曲时。因此,进入眼睛的光…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...



